【2.排序算法】
排序是算法中的基础,比C高级的语言一般都可调用其自带的库函数来实现,不过掌握其实现过程是必备的。
排序一般可以分为以下几类:
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序
- 归并排序
- 快速排序
- 堆排序
- 计数排序
- 桶排序
- 基数排序
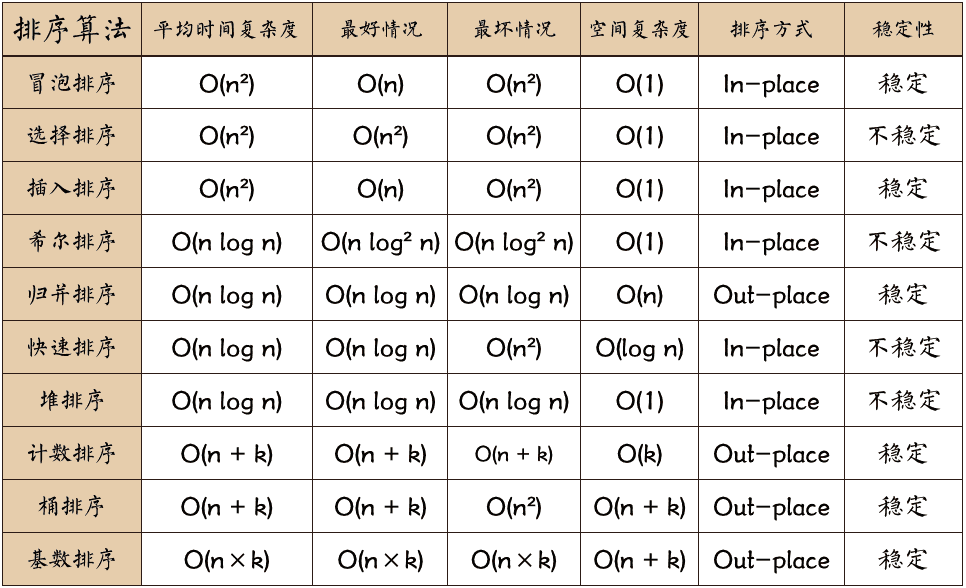
以上排序算法的时间复杂度、空间复杂度等如下:
排序算法——编程题;链接https://blog.csdn.net/kh971024/article/details/104195723
目录
2.1冒泡排序
2.1.1算法步骤
2.1.2动图演示
2.1.3代码
2.2选择排序
2.2.1算法步骤
2.2.2动图演示
2.2.3代码
2.3插入排序
2.3.1算法步骤
2.3.2动图演示
2.3.3代码
2.4希尔排序
2.4.1算法步骤
2.4.2动图演示
2.4.3代码
2.5归并排序
2.5.1算法步骤
2.5.2动图演示
2.5.3代码
2.6快速排序
2.6.1算法步骤
2.6.2代码
2.1冒泡排序
冒泡排序(Bubble Sort)也是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
2.1.1算法步骤
比较相邻的元素。如果第一个比第二个大,就交换他们两个。
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
最快:已经是正序
最慢:反序
2.1.2动图演示
2.1.3代码
用的最基本的数据,并没有用C++的容器
#include
using namespace std;
void bubble_sort(int arr[], int len){
for(int i = 0; i < len - 1; i++){
for(int j = 0; j < len - i - 1; j++){
if(arr[j] > arr[j + 1])
swap(arr[j], arr[j + 1]);
}
}
}
int main() {
int arr[] = {12, 7, 35, 2, 30, 23};
int len = (int) sizeof(arr) / sizeof(*arr);
bubble_sort(arr, len);
for(int i = 0; i < len; i++){
cout << arr[i] << " ";
}
return 0;
} 改进的冒泡排序:增加isSorted作为标记,当排序过程中没有元素交换,则认为排序完成,直接跳出大循环
void bubble_sort(int arr[], int len){
for(int i = 0; i < len - 1; i++){
bool isSorted = true;
for(int j = 0; j < len - i - 1; j++){
if(arr[j] > arr[j + 1])
swap(arr[j], arr[j + 1]);
isSorted = false;
}
if(isSorted)
break;
}
}
int main() {
int arr[] = {12, 7, 35, 2, 30, 23, 0, 17};
int len = (int) sizeof(arr) / sizeof(*arr);
bubble_sort(arr, len);
for(int i = 0; i < len; i++){
cout << arr[i] << " ";
}
return 0;
}2.2选择排序
选择排序是一种简单直观的排序算法,无论什么数据进去都是 O(n²) 的时间复杂度。所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间。
2.2.1算法步骤
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕。
2.2.2动图演示
2.2.3代码
void selection_sort(int arr[], int len){
//每次从未排序数组中选择最小值与当前值交换
for(int i = 0; i < len; i++){
int min = i;
for(int j = i + 1; j < len; j++){
if(arr[j] < arr[min])
min = j;
}
swap(arr[min], arr[i]);
}
}
int main(){
int arr[] = {12, 7, 35, 2, 30, 23, 0, 17};
int len = (int) sizeof(arr) / sizeof(*arr);
selection_sort(arr, len);
for(int i = 0; i < len; i++){
cout << arr[i] << " ";
}
return 0;
}2.3插入排序
插入排序是一种最简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
适用于链表和数组两种存储方式
2.3.1算法步骤
将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
2.3.2动图演示
2.3.3代码
void insertion_sort(int arr[], int len){
for(int i = 1; i < len; i++){
int key = arr[i];
int j = i - 1; // j从已排序数组最末尾开始,这样可以边后移边查找
while((j >= 0) && (key < arr[j])){
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = key;//j最后位置的num <= key
}
}
int main(){
int arr[] = {12, 7, 35, 2, 30, 23, 0, 17};
int len = (int) sizeof(arr) / sizeof(*arr);
insertion_sort(arr, len);
for(int i = 0; i < len; i++){
cout << arr[i] << " ";
}
return 0;
}2.4希尔排序
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。
希尔排序是基于插入排序的以下两点性质而提出改进方法的:
- 插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率;
- 但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位;
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
2.4.1算法步骤
选择一个增量序列 t1,t2,……,tk,其中 ti > tj, tk = 1;
按增量序列个数 k,对序列进行 k 趟排序;
每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
比如可以将初始增量设为 len / 2,每趟排序后再将增量 / 2,直至为1。
2.4.2动图演示
2.4.3代码
void shell_sort(int arr[], int len){
int gap = len / 2;
while (gap >= 1){
for(int index = gap; index < len; index++){
for(int i = index; i < len; i = i + gap){
//以下即为插入排序
int j = i - gap;
int key = arr[i];
while((j >= 0) && (key < arr[j])){
arr[j + gap] = arr[j];
j = j - gap;
}
arr[j + gap] = key;
}
}
gap = gap / 2;
}
}
int main(){
int arr[] = {12, 7, 35, 2, 30, 23, 0, 17, 1, 10, 9};
int len = (int) sizeof(arr) / sizeof(*arr);
shell_sort(arr, len);
for(int i = 0; i < len; i++){
cout << arr[i] << " ";
}
return 0;
}2.5归并排序
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。(空间换时间)
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
- 自上而下的递归
- 自下而上的迭代
2.5.1算法步骤
-
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
-
设定两个指针,最初位置分别为两个已经排序序列的起始位置;
-
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
-
重复步骤 3 直到某一指针达到序列尾;
-
将另一序列剩下的所有元素直接复制到合并序列尾。
2.5.2动图演示
2.5.3代码
递归算法
void Merge(vector &arr, int low, int mid, int high){
//分配两个有序序列空间
vector temp(high - low + 1);
//low为第1有序区的第1个元素,i指向第1个元素, mid为第1有序区的最后1个元素
int i = low, j = mid + 1, k = 0;
while(i <= mid && j <= high){
if(arr[i] <= arr[j]){
//较小的先存进去
temp[k++] = arr[i++];
} else{
temp[k++] = arr[j++];
}
}
while(i <= mid){
temp[k++] = arr[i++];
}
while(j <= high){
temp[k++] = arr[j++];
}
//将排序好的数据存回arr
for(i = low, k = 0; i <= high; i++, k++){
arr[i] = temp[k];
}
}
void Merge_sort(vector &arr, int low, int high){
if(low < high){
int mid = (low + high) / 2; //比如下标5和7的中间下标为(5+7)/2=6
Merge_sort(arr, low, mid);
Merge_sort(arr, mid + 1, high);
Merge(arr, low, mid, high);
}
}
int main(){
vector arr = {12, 7, 35, 2, 30, 23, 0, 17, 1, 10, 9};
Merge_sort(arr, 0, arr.size() - 1);
auto iter = arr.begin();
for(iter; iter != arr.end(); iter++){
cout << *iter << " ";
}
} 2.6快速排序
快速排序使用分治法(Divide and conquer)策略来把一个串行(list)分为两个子串行(sub-lists)。
快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看,快速排序应该算是在冒泡排序基础上的递归分治法。
快速排序的名字起的是简单粗暴,因为一听到这个名字你就知道它存在的意义,就是快,而且效率高!它是处理大数据最快的排序算法之一了。
2.6.1算法步骤
-
从数列中挑出一个元素,称为 "基准"(pivot);
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作,使用交换元素完成;
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
2.6.2代码
int Partition(vector &arr, int low, int high){
int pivot = low; //选择首位元素作为基准
while (low < high){
while (low < high && arr[high] >= arr[pivot])
high--;
while (low < high && arr[low] <= arr[pivot])
low++;
swap(arr[low], arr[high]);
}
swap(arr[pivot], arr[low]);
return low;
}
void QuickSort(vector &arr, int low, int high){
if(low < high){
int pivot = Partition(arr, low, high);
QuickSort(arr, low, pivot - 1);
QuickSort(arr, pivot + 1, high);
}
}
int main(){
vector arr = {12, 7, 35, 2, 30, 23, 0, 17, 1, 10, 9, 26, 5};
QuickSort(arr, 0, arr.size() - 1);
auto iter = arr.begin();
for(iter; iter != arr.end(); iter++){
cout << *iter << " ";
}
}