LSTM与BI-LSTM

从RNN到LSTM

在RNN模型里，我们讲到了RNN具有如下的结构，每个序列索引位置t都有一个隐藏状态h(t)。
　　　　如果我们略去每层都有的$o^{(t)},L^{(t)},y^{(t)}$，则RNN的模型可以简化成如下图的形式：
　　　　
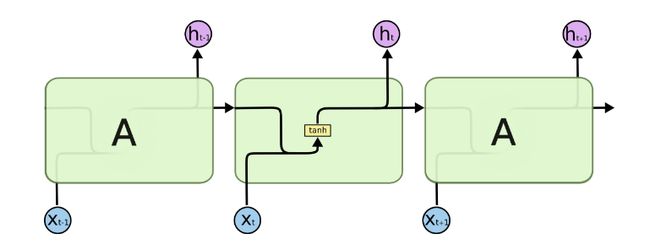
　　　　图中可以很清晰看出在隐藏状态$h^{(t)}$由$x^{(t)}$和$h^{(t-1)}$得到。得到h(t)后一方面用于当前层的模型损失计算，另一方面用于计算下一层的$h^{(t+1)}$。
　　　　由于RNN梯度消失的问题，大牛们对于序列索引位置t的隐藏结构做了改进，可以说通过一些技巧让隐藏结构复杂了起来，来避免梯度消失的问题，这样的特殊RNN就是我们的LSTM。由于LSTM有很多的变种，这里我们以最常见的LSTM为例讲述。LSTM的结构如下图：
　　　　

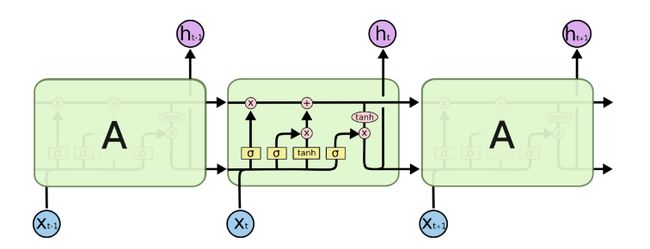
LSTM模型结构剖析

上面我们给出了LSTM的模型结构，下面我们就一点点的剖析LSTM模型在每个序列索引位置t时刻的内部结构。

从上图中可以看出，在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态h(t)，还多了另一个隐藏状态，如图中上面的长横线。这个隐藏状态我们一般称为细胞状态(Cell State)，记为$C^{(t)}$。如下图所示：

除了细胞状态，LSTM图中还有了很多奇怪的结构，这些结构一般称之为门控结构(Gate)。LSTM在在每个序列索引位置t的门一般包括遗忘门，输入门和输出门三种。下面我们就来研究上图中LSTM的遗忘门，输入门和输出门以及细胞状态。

LSTM之遗忘门

遗忘门（forget gate）顾名思义，是控制是否遗忘的，在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图所示：

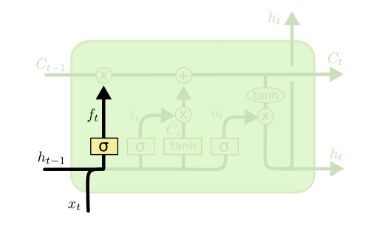
图中输入的有上一序列的隐藏状态$h^{(t-1)}$和本序列数据$x^{(t)}$，通过一个激活函数，一般是sigmoid，得到遗忘门的输出$f^{(t)}$。由于sigmoid的输出f(t)在[0,1]之间，因此这里的输出$f^{(t)}$代表了遗忘上一层隐藏细胞状态的概率。用数学表达式即为：
$$f^{(t)}=\sigma (W_f{h}^{(t-1)}+U_f{x}^{(t)}+b_f)$$
其中Wf,Uf,bf为线性关系的系数和偏倚，和RNN中的类似。σ为sigmoid激活函数。

LSTM之输入门

输入门（input gate）负责处理当前序列位置的输入，它的子结构如下图：
　　　　
　　　　从图中可以看到输入门由两部分组成，第一部分使用了sigmoid激活函数，输出为i(t),第二部分使用了tanh激活函数，输出为a(t), 两者的结果后面会相乘再去更新细胞状态。用数学表达式即为：
$$i^{(t)}=\sigma (W_i{h}^{(t-1)}+U_i{x}^{(t)}+b_i)$$
$$a^{(t)}=tanh(W_a{h}^{(t-1)}+U_a{x}^{(t)}+b_a)$$
其中$W_i,U_i,b_i,W_a,U_a,b_a,$为线性关系的系数和偏倚，和RNN中的类似。σ为sigmoid激活函数。

LSTM之细胞状态更新

在研究LSTM输出门之前，我们要先看看LSTM之细胞状态。前面的遗忘门和输入门的结果都会作用于细胞状态C(t)。我们来看看从细胞状态C(t−1)如何得到C(t)。如下图所示：

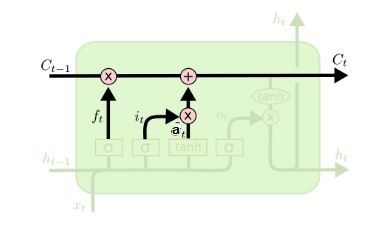
细胞状态$C^{(t)}$由两部分组成，第一部分是$C^{(t-1)}$和遗忘门输出$f^{(t)}$的乘积，第二部分是输入门的$i^{(t)}$和$a^{(t)}$的乘积，即：
$$C^{(t)}=C^{(t-1)}\odot f^{(t)}+i^{(t)}\odot a^{(t)}$$
其中，⊙为Hadamard积，在DNN中也用到过

LSTM之输出门

有了新的隐藏细胞状态C(t)，我们就可以来看输出门了，子结构如下：
　　　　
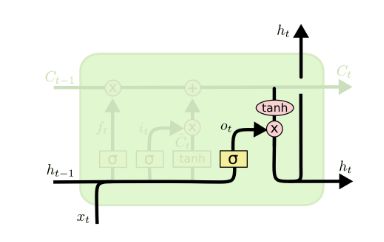
　　　　从图中可以看出，隐藏状态$h^{(t)}$的更新由两部分组成，第一部分是o(t), 它由上一序列的隐藏状态$h^{(t-1)}$和本序列数据$x^{(t)}$，以及激活函数sigmoid得到，第二部分由隐藏状态C(t)和tanh激活函数组成, 即：
　　　　$$o^{(t)}=\sigma (W_o{h}^{(t-1)}+U_o{x}^{(t)}+b_o)$$
　　　　$$h^{(t)}=o^{(t)}\odot tanh(C^{(t)})$$

LSTM前向传播算法

现在我们来总结下LSTM前向传播算法。LSTM模型有两个隐藏状态$h^{(t)},C^{(t)}$，模型参数几乎是RNN的4倍，因为现在多了$W_f,U_f,b_f,W_a,U_a,b_a,W_i,U_i,b_i,W_o,U_o,b_o$这些参数。

前向传播过程在每个序列索引位置的过程为：

1）更新遗忘门输出：
$f^{(t)}=\sigma (W_f{h}^{(t-1)}+U_f{x}^{(t)}+b_f)$
　　　　2）更新输入门两部分输出：
$i^{(t)}=\sigma (W_i{h}^{(t-1)}+U_i{x}^{(t)}+b_i)$
$a^{(t)}=tanh(W_a{h}^{(t-1)}+U_a{x}^{(t)}+b_a)$
　　　　3）更新细胞状态：
$C^{(t)}=C^{(t-1)}\odot f^{(t)}+i^{(t)}\odot a^{(t)}$
　　　　4）更新输出门输出：
$$o^{(t)}=\sigma (W_o{h}^{(t-1)}+U_o{x}^{(t)}+b_o)$$
$$h^{(t)}=o^{(t)}\odot tanh(C^{(t)})$$
　　　　5）更新当前序列索引预测输出：
$${\hat{y}}^{(t)}=\sigma (V{h}^{(t)}+c)$$

LSTM反向传播算法推导关键点

有了LSTM前向传播算法，推导反向传播算法就很容易了， 思路和RNN的反向传播算法思路一致，也是通过梯度下降法迭代更新我们所有的参数，关键点在于计算所有参数基于损失函数的偏导数。

在RNN中，为了反向传播误差，我们通过隐藏状态$h^{(t)}$的梯度${\delta }^{(t)}$一步步向前传播。在LSTM这里也类似。只不过我们这里有两个隐藏状态$h^{(t)}$和C(t)。这里我们定义两个δ，即：
$${\delta }_h^{(t)}=\frac{\partial L}{\partial h^{(t)}}$$
$${\delta }_C^{(t)}=\frac{\partial L}{\partial C^{(t)}}$$
　　　　为了便于推导，我们将损失函数L(t)分成两块，一块是时刻t位置的损失l(t)，另一块是时刻t之后损失L(t+1)，即：
　　　　$$L(t)=\{\begin{array}{ll}l(t)+L(t+1)& \text{if}t<\tau \\ l(t)& \text{if}t=\tau \end{array}$$
　　　　而在最后的序列索引位置τ的${\delta }_h^{(\tau )}$和 ${\delta }_C^{(\tau )}$为：
　　　　$${\delta }_h^{(\tau )}=(\frac{\partial O^{(\tau )}}{\partial h^{(\tau )}}{)}^T\frac{\partial L^{(\tau )}}{\partial O^{(\tau )}}=V^T({\hat{y}}^{(\tau )}-y^{(\tau )})$$
　　　　接着我们由${\delta }_C^{(t+1)},{\delta }_h^{(t+1)}$反向推导${\delta }_h^{(t)},{\delta }_C^{(t)}$

${\delta }_h^{(t)}$的梯度由本层t时刻的输出梯度误差和大于t时刻的误差两部分决定，即：
$${\delta }_h^{(t)}=\frac{\partial L}{\partial h^{(t)}}=\frac{\partial l(t)}{\partial h^{(t)}}+(\frac{\partial h^{(t+1)}}{\partial h^{(t)}}{)}^T\frac{\partial L(t+1)}{\partial h^{(t+1)}}=V^T({\hat{y}}^{(t)}-y^{(t)})+(\frac{\partial h^{(t+1)}}{\partial h^{(t)}}{)}^T{\delta }_h^{(t+1)}$$
　　　　整个LSTM反向传播的难点就在于$\frac{\partial h^{(t+1)}}{\partial h^{(t)}}$这部分的计算。仔细观察，由于$h^{(t)}=o^{(t)}\odot tanh(C^{(t)})$ 在第一项o(t)中，包含一个h的递推关系，第二项tanh(C(t))就复杂了，tanh函数里面又可以表示成：
$$C^{(t)}=C^{(t-1)}\odot f^{(t)}+i^{(t)}\odot a^{(t)}$$
tanh函数的第一项中，f(t)包含一个h的递推关系，在tanh函数的第二项中，i(t)和a(t)都包含h的递推关系，因此，最终$\frac{\partial h^{(t+1)}}{\partial h^{(t)}}$这部分的计算结果由四部分组成。即：

$$\Delta C=o^{(t+1)}\odot [1-tan{h}^2(C^{(t+1)})]$$
$$\frac{\partial h^{(t+1)}}{\partial h^{(t)}}=W_o^T[o^{(t+1)}\odot (1-o^{(t+1)})\odot tanh(C^{(t+1)})]+W_f^T[\Delta C\odot f^{(t+1)}\odot (1-f^{(t+1)})\odot C^{(t)}]+W_a^T\{\Delta C\odot i^{(t+1)}\odot [1-(a^{(t+1)}{)}^2]\}+W_i^T[\Delta C\odot a^{(t+1)}\odot i^{(t+1)}\odot (1-i^{(t+1)})]$$
　　　　而${\delta }_C^{(t)}$的反向梯度误差由前一层${\delta }_C^{(t+1)}$的梯度误差和本层的从$h^{(t)}$传回来的梯度误差两部分组成，即：
$${\delta }_C^{(t)}=(\frac{\partial C^{(t+1)}}{\partial C^{(t)}}{)}^T\frac{\partial L}{\partial C^{(t+1)}}+(\frac{\partial h^{(t)}}{\partial C^{(t)}}{)}^T\frac{\partial L}{\partial h^{(t)}}=(\frac{\partial C^{(t+1)}}{\partial C^{(t)}}{)}^T{\delta }_C^{(t+1)}+{\delta }_h^{(t)}\odot o^{(t)}\odot (1-tan{h}^2(C^{(t)}))={\delta }_C^{(t+1)}\odot f^{(t+1)}+{\delta }_h^{(t)}\odot o^{(t)}\odot (1-tan{h}^2(C^{(t)}))$$
　　　　有了${\delta }_h^{(t)}$和${\delta }_C^{(t)}$， 计算这一大堆参数的梯度就很容易了，这里只给出Wf的梯度计算过程，其他的$U_f,b_f,W_a,U_a,b_a,W_i,U_i,b_i,W_o,U_o,b_o，V,c$的梯度大家只要照搬就可以了。
$$\frac{\partial L}{\partial W_f}=\sum _{t=1}^{\tau }[{\delta }_C^{(t)}\odot C^{(t-1)}\odot f^{(t)}\odot (1-f^{(t)})](h^{(t-1)}{)}^T$$

BiLSTM

前向的LSTM与后向的LSTM结合成BiLSTM。
我们对“我爱中国”这句话进行编码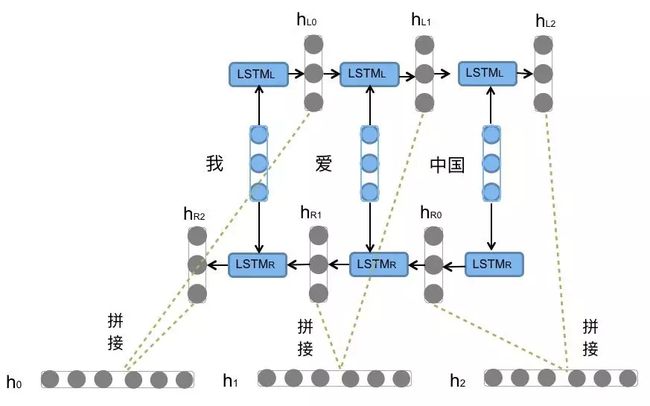
前向的依次输入“我”，“爱”，“中国”得到三个向量{$h_{L0},h_{L1},h_{L2}$}。后向的依次输入“中国”，“爱”，“我”得到三个向量{$h_{R0},h_{R1},h_{R2}$}。最后将前向和后向的隐向量进行拼接得到{$[h_{L0},h_{R2}][h_{L1},h_{R1}],[h_{L2},h_{R0}]$}，即{$h_0,h_1,h_2$}。