面向初学者的机器学习教程：从零开始使用Python实现一个神经网络

本文内容大致翻译自Machine Learning for Beginners: An Introduction to Neural Networks，我个人修改或添加了部分内容，若感觉价值不高，请跳过或参阅原文。

这篇文章关注的，更多是思想和理论方法，而不是神经网络工具的使用教程。如果你想要学习算法理论，这篇文章是合适的。但如果你想速成使用方法，这篇文章是不适合你的。

面向初学者的机器学习教程：神经网络简介

简单解释神经网络如何工作，并且从零开始使用Python实现一个神经网络。

神经网络可能并没有你想象的那么复杂。虽然“神经网络”这个词经常被用作流行语，但实际上它比人们往往想象的要简单得多。

这篇文章是为完全初学者准备的，即使零基础的小白也是适用的。我们将了解神经网络如何工作，并且从零开始使用Python实现一个神经网络（使用了numpy包来完成数学运算）。

一个很好玩的是：我针对这篇文章制作了一个基于Jupyter Notrbook的动态教程，这里就是playground示例。

现在开始我们的教程！

1. 制作一个神经元

1.1 什么是神经元？

首先，我们要知道什么是神经元。它是神经网络的基本单位，用来接受输入，做一些数学运算，然后产生一个输出。这是一个2输入神经元的示意图:

你完全可以把它想象成一个函数，在这个神经元（函数）里发生了三个运算：

1. 每个输入分别乘以一个权重w1,w2（weight）

   $$x_1\to x_1\ast w_1$$

   $$x_2\to x_2\ast w_2$$

2. 将上一步的结果加起来，再加上一个偏置b（bias）

   $$(x_1\times w_1)+(x_2\times w_2)+b$$

3. 把上一步的结果带入激活函数（activation function）中进行计算。于是就可以把输出表示为：

   $$y=f(x_1\ast w_1+x_2\ast w_2+b)$$

看到这里，你可能有两个疑问：

1. 激活函数f(x)是什么？

   激活函数的作用是将无限制的输入转换为可预测形式的输出。它是一类函数的总称，其中一种很常用的激活函数是sigmoid函数，它能将变量映射到0,1之间，表达式为
   $$f(x)=\frac{1}{1+e^{-x}}$$
   在坐标轴上表现是这样的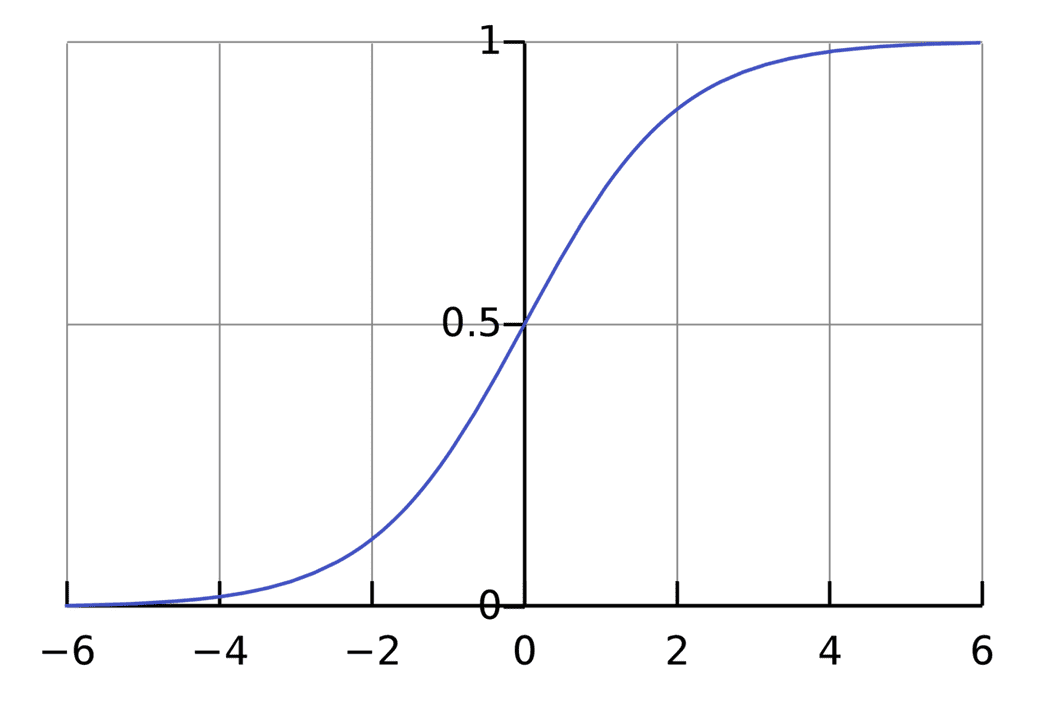

   sigmoid函数的输出介于0和1，我们可以理解为它把 (−∞,+∞) 范围内的数压缩到 (0, 1)以内。正值越大输出越接近1，负向数值越大输出越接近0。

2. 神经元不就是个函数吗？

   是的，神经元就是个函数。将上面的几步整理起来，如果你选取Sigmoid作激活函数的话，一个2输入的神经元就是：

   $$f(x_1,x_2)=\frac{1}{1+e^{x_1\ast w_1+x_2\ast w_2+b}}$$

1.2 神经元实例

接下来是一个简单的例子，来帮助你理解什么是神经元：

假设我们有一个以Sigmoid作激活函数的2输入的神经元，它具有这样的参数：

$$w=[0,1]$$

$$b=4$$

(w=[0,1]是w1=0,w2=1使用向量书写时的样子)

那么我们就可以使用这个神经元来做计算了，比如，我们输入x = [2,3],那么计算过程就是(使用向量点乘表示)：

$$\begin{array}{rl}result& =Sigmoid(x_1\ast w_1+x_2\ast w_2+b)\\ & =Sigmoid([0,1]\cdot [2,3]+4)\\ & =\frac{1}{1+e^7}\approx 0.999\end{array}$$

即神经元在输入为[2,3]的时候输出为0.999。这样计算是从输入正向传递以获得输出，这在神经网络中称为正向传播过程。

1.3 神经元代码实现

我们这里使用了NumPy来完成一些数学计算:

import numpy as np

def sigmoid(x):
  # Sigmoid激活函数：f(x) = 1 / (1 + e^(-x))
  return 1 / (1 + np.exp(-x))

class Neuron:
  def __init__(self, weights, bias):
    self.weights = weights
    self.bias = bias

  def feedforward(self, inputs):
    # 给输入赋权，添加偏置，然后带入激活函数
    total = np.dot(self.weights, inputs) + self.bias
    return sigmoid(total)

然后运行一下测试：

weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 4                   # b = 4
n = Neuron(weights, bias)

x = np.array([2, 3])       # x1 = 2, x2 = 3
print(n.feedforward(x))    # 0.9990889488055994

2. 搭建神经网络

2.1 什么是神经网络?

神经网络只不过是一群连接在一起的神经元。下面是一个简单的神经网络的示意图:

这个网络有一个包含两个输入的输入层(Input Layer)，一个包括两个神经元(h1,h2)的隐藏层(Hidden Layer)，一个包含一个神经元(o1)的输出层(Output Layer)。连线表示o1的输入就是h1,h2的输出。

正是这种上层输出作为下层输入的特性，连接起了神经网络。

隐藏层(Hidden Layer)：输入层和输出层之间的所有层(Layer)都叫隐藏层，一个神经网络中可能有多个隐藏层。

2.2 神经网络上的正向传播实例

正向传播(feedforward):从输入正向传递以获得输出的过程(简单来说就是从左往右计算)

我们就使用上图所示的神经网络，并假设所有神经元的权重都为[0,1],偏置都为0，激活都使用Sigmoid函数。

那么在两个输入都为[2,3]的时候，计算输出的过程就为：

$$\begin{array}{rl}{h}_1=h_2& =Sigmoid(w\cdot x+b)\\ & =Sigmoid([0,1]\cdot [2,3]+0)\\ & =Sigmoid(3)=0.9526\end{array}$$
$$\begin{array}{rl}{o}_1& =Sigmoid(w\cdot [h_1,h_2]+b)\\ & =Sigmoid([0,1]\cdot [0.9526,0.9526]+0)\\ & =Sigmoid(0.9526)=0.7216\end{array}$$

即神经网络在输入为[2,3]的时候输出为0.7216。

神经网络可以具有任意数量的层，这些层中具有任意数量的神经元。且基本思想保持不变：通过网络中的神经元正向传递以获得输出。在下文中，我们将继续使用上图所示的网络来完成表述。

2.3 正向传播的代码实现

依旧是这个神经网络:

实现代码：

import numpy as np

# ... 神经元的实现需要粘贴在这里

class OurNeuralNetwork:
  '''
  一个神经元，它具有:
    - 2*输入
    - 1*隐藏层 = 2*神经元 = (h1, h2)
    - 1*输出层 = 1*神经元 = (o1)

  每个神经元都具有相同的权重和偏置：
    - 权重w = [0, 1]
    - 偏置b = 0
  '''
  def __init__(self):
    weights = np.array([0, 1])
    bias = 0

    # 神经元的实现在1.2中提到
    self.h1 = Neuron(weights, bias)
    self.h2 = Neuron(weights, bias)
    self.o1 = Neuron(weights, bias)

  def feedforward(self, x):
    out_h1 = self.h1.feedforward(x)
    out_h2 = self.h2.feedforward(x)

    # o1 的输入就是 h1 和 h2的输出
    out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))

    return out_o1

测试代码：

network = OurNeuralNetwork()
x = np.array([2, 3])
print(network.feedforward(x)) # 0.7216325609518421

最终我们能获得0.7216作为正向传播输出。

3.训练神经网络

3.1 训练任务

假设我们已经具有这样的数据：

名字	体重(磅)	身高(英尺)	性别
张一	133	65	女
王二	160	72	男
刘三	152	70	男
李四	120	60	女

我们的任务是训练一个神经网络，使它能通过一个人的身高体重来预测人的性别。

3.2 损失函数

3.2.1 什么是损失函数

在我们培训我们的网络之前，我们首先需要选取一种方法来量化神经网络预测得有多“好”，这样它就可以尝试做得“更好”。我们需要的就是损失函数。

本文将使用的是均方误差(MSE)损失:

$$MSE=\frac{1}{n}\sum _{i=1}^n(y_{true}-y_{pred}{)}^2$$

• n 是样本数量，在实例中是4(张一, 王二, 刘三, 李四)
• y 是目标量，在实例中是性别
• $y_{true}$ 是真实的结果(正确答案)，在实例中对张一来说就是1
• $y_{pred}$ 是预测的结果，就是神经网络输出的结果。

$(y_{true}-y_{pred}{)}^2$ 被称作方差(平方误差)，我们这里的损失函数只是取所有方差的平均值(故名“均方差”“mean squared error”)。预测效果越好，损失函数的值就会越低。

也就是：

• 效果好 = 损失小
• 训练神经网络 = 降低损失

3.2.2 损失函数计算实例

我们假设我们的神经网络输出全为0，则损失会有多大？

姓名	真实值	预测值	方差
张一	1	0	1
王二	0	0	0
刘三	0	0	0
李四	1	0	1

$$MSE=\frac{1}{4}(1+0+0+1)=0.5$$

3.2.3 损失函数计算实现

import numpy as np

def mse_loss(y_true, y_pred):
  # y_true 和 y_pred 是同样长的numpy.array
  return ((y_true - y_pred) ** 2).mean()

测试代码：

y_true = np.array([1, 0, 0, 1])
y_pred = np.array([0, 0, 0, 0])

print(mse_loss(y_true, y_pred)) # 0.5

3.3 数据预处理

我们用0表示男性，用1表示女性，并调整数据，使其更容易使用:

名字	体重(135)	身高(66)	性别
张一	-2	-1	1
王二	25	6	0
刘三	17	4	0
李四	-15	-6	1

135和66是随意选取的偏移量，以使数据更优美，偏移以及此处未用到的归一化都是常用的调整手段.

3.4 反向传播

3.4.1 什么是反向传播？

我们现在有一个明确的目标:最小化神经网络的损失。并且我们还知道可以通过改变神经网络的权重和偏置来影响它的预测结果，但我们如何才能实现目标呢?

为了简单说明方法，先假设我们的数据集中只有张一:

名字	体重(135)	身高(66)	性别
张一	-2	-1	1

计算初始均方差：

$$\begin{array}{rl}MSE& =\frac{1}{1}\sum _{i=1}^n(y_{true}-y_{pred}{)}^2\\ & =(y_{true}-y_{pred}{)}^2\\ & =(1-y_{pred}{)}^2\end{array}$$

另一种考虑损失的方法是将损失看作权重和偏置的函数。我们先在神经网络中标记每个权重和偏置:

然后，我们可以将损失写成一个多元函数:

$$Loss(w_1,w_2,w_3,w_4,w_5,w_6,b_1,b_2,b_3)$$

假设我们想要调整$w_1$,那么Loss将会如何随之改变？这时候你就应该想到了偏导数$\frac{\partial Loss}{\partial w_1}$。这不就是偏导数的定义吗？

这时候就需要一些数学推导了。

首先,使用链式法则对偏导数变形。

$$\frac{\partial Loss}{\partial w_1}=\frac{\partial Loss}{\partial y_{pred}}\ast \frac{\partial y_{pred}}{\partial w_1}$$

由于我们可以计算Loss的值，所以$\frac{\partial Loss}{\partial y_{pred}}$是我们可以求得的

$$\frac{\partial Loss}{\partial y_{pred}}=\frac{\partial (1-y_{pred}{)}^2}{\partial y_{pred}}=-2(1-y_{pred})$$

然后我们来想办法解决$\partial y_{pred}\partial w_1$，使用$h_1,h_2,o_1$来分别表示各神经元的输出，那么：

$$y_{pred}=o_1=Sigmoid(w_5\ast h_1+w_6\ast h_2+b_3)$$

由于$w_1$只影响$h_1$，而对$h_2$无影响，那么：

$$\frac{\partial y_{pred}}{\partial w_1}=\frac{\partial y_{pred}}{\partial h_1}\ast \frac{\partial h_1}{\partial w_1}$$

$$\frac{\partial y_{pred}}{\partial h_1}=w_5\ast Sigmoid\prime (w_5{h}_1+w_6{h}_2+b_3)$$

对$\frac{\partial h_1}{\partial w_1}$，我们做相同的处理：

$$h_1=Sigmoid(w_1{x}_1+w_2{x}_2+b_1)$$

$$\frac{\partial h_1}{\partial w_1}=x_1\ast Sigmoid\prime (w_1{x}_1+w_2{x}_2+b_1)$$

由于上面用到了，把Sigmoid函数导函数求出来（这里暂时不用这个求导结果来化简上面的式子）：

$$\begin{array}{rl}Sigmoid\prime (x)& =(\frac{1}{1+e^{-x}})\prime \\ & =\frac{e^{-x}}{(1+e^{-x}{)}^2}\\ & =Sigmoid(x)\ast (1-Sigmoid(x))\end{array}$$

于是，我们就把$\frac{\partial Loss}{\partial w_1}$给成功拆成了我们能计算的几部分：

$$\frac{\partial Loss}{\partial w_1}=\frac{\partial Loss}{\partial y_{pred}}\ast \frac{\partial y_{pred}}{\partial h_1}\ast \frac{\partial h_1}{\partial w_1}$$

这样逆向计算偏导数的过程称为反向传播(“backpropagation”)。

3.4.2 反向传播实例

为了简化计算，我们继续假设我们的数据集中只有张一:

名字	体重(135)	身高(66)	性别
张一	-2	-1	1

把所有权重初始化为1，偏置初始化为0。然后进行一次正向传播。

$$\begin{array}{rl}{h}_1=h_2& =Sigmoid([w1,w2]\cdot [x1,x2]+b1)\\ & =Sigmoid(-2-1+0)\\ & =Sigmoid(-3)=0.0474\end{array}$$

$$\begin{array}{rl}{o}_1& =Sigmoid([w_5,w_6]\cdot [h_1,h_2]+b3)\\ & =Sigmoid(0.0474+0.0474+0)\\ & =Sigmoid(0.0948)=0.524\end{array}$$

神经网络的结果为0.524，意思是并不能明显判断出是男(1)还是女(0)。

这样以后我们进行一次反向传播。也就是计算$\frac{\partial Loss}{\partial w_1}$.

（下面这些计算的推导都在3.4.1中）

$$\frac{\partial Loss}{\partial w_1}=\frac{\partial Loss}{\partial y_{pred}}\ast \frac{\partial y_{pred}}{\partial h_1}\ast \frac{\partial h_1}{\partial w_1}$$

$$\begin{array}{rl}\frac{\partial Loss}{\partial y_{pred}}& =-2(1-y_{pred})\\ & =-2(1-0.524)=-0.952\end{array}$$

$$\begin{array}{rl}\frac{\partial y_{pred}}{\partial h_1}& =w_5\ast Sigmoid\prime (w_5{h}_1+w_6{h}_2+b_3)\\ & =1\ast Sigmoid\prime (0.0474+0.0474+0)\\ & =Sigmoid(0.0948)\ast (1-Sigmoid(0.0948))\\ & =0.249\end{array}$$

$$\begin{array}{rl}\frac{\partial h_1}{\partial w_1}& =x_1\ast Sigmoid\prime (w_1{x}_1+w_2{x}_2+b_1)\\ & =-2\ast Sigmoid\prime (-2-1+0)\\ & =-2\ast Sigmoid(-3)\ast (1-Sigmoid(-3))\\ & =-0.0904\end{array}$$

$$\frac{\partial Loss}{\partial w_1}=-0.952\ast 0.249\ast (-0.0904)=0.0214$$

完成了这次反向传播，我们就知道了改变w1时对Loss的影响大小：0.0214。

3.5 随机梯度下降算法

现在我们将使用一种称为随机梯度下降(SGD)的优化算法，它会告诉我们如何改变权重和偏置以最小化损失。大概就是这个更新方程:

$$w_1\leftarrow w_1-\eta \frac{\partial Loss}{\partial w_1}$$

η : 学习速率(Learning rate)，用来控制训练时梯度下降的速度。(并不是越大越好！)

我们做的就只是把w1减去$\eta \frac{\partial Loss}{\partial w_1}$。

• 若$\eta \frac{\partial Loss}{\partial w_1}$大于0，w1会增加，以降低Loss（η合适时）
• 若$\eta \frac{\partial Loss}{\partial w_1}$小于0，w2会减少，以降低Loss（η合适时）

如果我们对神经网络中的每一个权重和偏置都这样做，损失就会慢慢降低，我们的神经网络的预测效果就会改善。
我们的训练流程如下:

1. 从数据集中选择一个示例（随机梯度下降算法要求我们每次只对一个样本进行操作）
2. 计算所有“损失对权重或偏置的偏导数”（引号用于辅助断句）
3. 更新权重或偏置（注意：这里不是算一个偏导更新一个参数，是全部一起更新）
4. 回到步骤1，直至Loss到达满意的区间

3.6 训练神经网络代码实现

名字	体重(135)	身高(66)	性别
张一	-2	-1	1
王二	25	6	0
刘三	17	4	0
李四	-15	-6	1

import numpy as np

def sigmoid(x):
  # sigmoid函数：f(x) = 1 / (1 + e^(-x))
  return 1 / (1 + np.exp(-x))

def deriv_sigmoid(x):
  # sigmoid函数的导数：f'(x) = f(x) * (1 - f(x))
  fx = sigmoid(x)
  return fx * (1 - fx)

def mse_loss(y_true, y_pred):
  # y_true 和 y_pred 是同样长的numpy.array
  return ((y_true - y_pred) ** 2).mean()

class OurNeuralNetwork:
   '''
  一个神经元，它具有:
    - 2*输入
    - 1*隐藏层 = 2*神经元 = (h1, h2)
    - 1*输出层 = 1*神经元 = (o1)

  每个神经元都具有相同的权重和偏置：
    - 权重w = [0, 1]
    - 偏置b = 0
  '''
  def __init__(self):
    # 权重
    self.w1 = np.random.normal()
    self.w2 = np.random.normal()
    self.w3 = np.random.normal()
    self.w4 = np.random.normal()
    self.w5 = np.random.normal()
    self.w6 = np.random.normal()

    # 偏置
    self.b1 = np.random.normal()
    self.b2 = np.random.normal()
    self.b3 = np.random.normal()

  def feedforward(self, x):
    # x 是len=2的numpy.array
    h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)
    h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)
    o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
    return o1

  def train(self, data, all_y_trues):
    '''
    - data 是(n x 2)的numpy.array,n是样本容量.
    - all_y_trues 是（n*1）的numpy.array，与data相对应
    '''
    learn_rate = 0.1 # 学习率
    #epoch：所有训练数据一次正向传播，向后传播，更新参数的过程
    epochs = 1000 # epoch次数

    for epoch in range(epochs):
      for x, y_true in zip(data, all_y_trues):
        # 正向传播
        sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
        h1 = sigmoid(sum_h1)

        sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
        h2 = sigmoid(sum_h2)

        sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
        o1 = sigmoid(sum_o1)
        y_pred = o1

        # 向后传播
        # d_L_d_w1 表示 " L对w1的偏导数"
        d_L_d_ypred = -2 * (y_true - y_pred)

        # 神经元 o1
        d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)
        d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)
        d_ypred_d_b3 = deriv_sigmoid(sum_o1)

        d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)
        d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)

        # 神经元 h1
        d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)
        d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)
        d_h1_d_b1 = deriv_sigmoid(sum_h1)

        # 神经元 h2
        d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)
        d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)
        d_h2_d_b2 = deriv_sigmoid(sum_h2)

        # 更新权重和偏置
        # 神经元 h1
        self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
        self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
        self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1

        # 神经元 h2
        self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3
        self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4
        self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2

        # 神经元 o1
        self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5
        self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6
        self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3

      # --- 每10epoch计算输出一次Loss
      if epoch % 10 == 0:
        y_preds = np.apply_along_axis(self.feedforward, 1, data)
        loss = mse_loss(all_y_trues, y_preds)
        print("Epoch %d loss: %.3f" % (epoch, loss))

测试代码：

# 数据集定义
data = np.array([
  [-2, -1],  # 张一
  [25, 6],   # 王二
  [17, 4],   # 刘三
  [-15, -6], # 李四
])
all_y_trues = np.array([
  1, # 张一
  0, # 王二
  0, # 刘三
  1, # 李四
])

# 训练!
network = OurNeuralNetwork()
network.train(data, all_y_trues)

于是我们就获得一个训练好的神经网络，接下来用它来预测一下：

# 用一些神经网络没见过的数据来做预测
emily = np.array([-7, -3]) # 128 pounds, 63 inches
frank = np.array([20, 2])  # 155 pounds, 68 inches
print("Emily: %.3f" % network.feedforward(emily)) # 0.951 - F
print("Frank: %.3f" % network.feedforward(frank)) # 0.039 - M

总结

完美！快速回顾一下我们在这篇文章中做的:

• 介绍了神经元，神经网络的组成部分。
• 在我们的神经元中使用Sigmoid激活函数。
• 意识到神经网络只是一些连接在一起的神经元。
• 创建了一个数据集，其中将体重和身高作为输入(或特性)，性别作为输出(或标签)。
• 学习了损失函数和均方误差损失。
• 意识到训练一个网络只是把它的损失函数值降到最低。
• 使用反向传播计算偏导数。
• 利用随机梯度下降法(SGD)对网络进行训练。

接下来进阶学习需要做的:

• 使用机器学习库(如Tensorflow、Keras和PyTorch)来训练更大/更好的神经网络。
• 发现Sigmoid以外的其他激活函数。
• 发现除随机梯度下降算法（SGD）之外的其他优化器。
• 学习彻底改变了计算机视觉的卷积神经网络。
• 学习经常用于自然语言处理(NLP)的递归神经网络。