python数据分析练习题
本次作业尝试使用ipython和jupyter的notebook功能来实现py代码。
首先是要配置环境,通过命令
pip install ipython
pip install jypyter
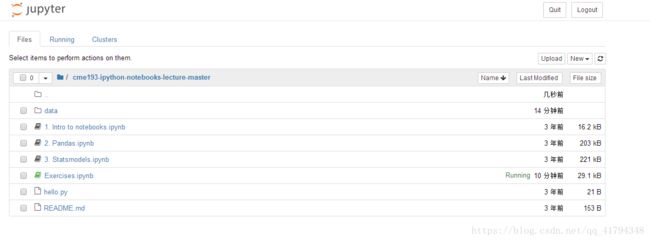
ipython notebook配置并打开notebook,下载作业文档,效果如下图所示:
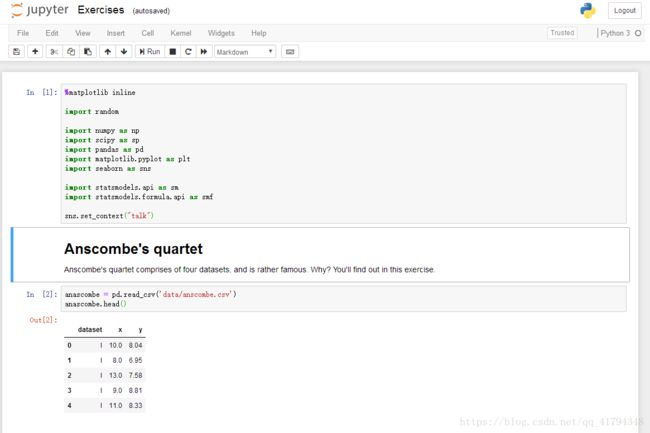
打开exercises.ipynb,完成作业。
1. :
For each of the four datasets...
- Compute the mean and variance of both x and y
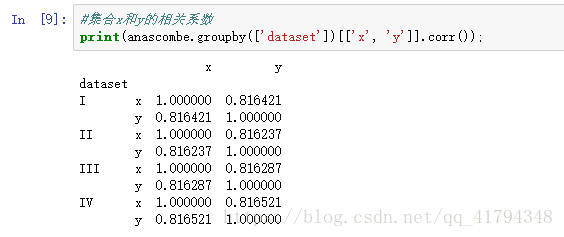
- Compute the correlation coefficient between x and y
- Compute the linear regression line: y=β0+β1x+ϵy=β0+β1x+ϵ (hint: use statsmodels and look at the Statsmodels notebook)
notebook上的代码和结果如下:
I
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.667
Model: OLS Adj. R-squared: 0.629
Method: Least Squares F-statistic: 17.99
Date: Tue, 12 Jun 2018 Prob (F-statistic): 0.00217
Time: 17:05:04 Log-Likelihood: -16.841
No. Observations: 11 AIC: 37.68
Df Residuals: 9 BIC: 38.48
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 3.0001 1.125 2.667 0.026 0.456 5.544
x 0.5001 0.118 4.241 0.002 0.233 0.767
==============================================================================
Omnibus: 0.082 Durbin-Watson: 3.212
Prob(Omnibus): 0.960 Jarque-Bera (JB): 0.289
Skew: -0.122 Prob(JB): 0.865
Kurtosis: 2.244 Cond. No. 29.1
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
II
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.666
Model: OLS Adj. R-squared: 0.629
Method: Least Squares F-statistic: 17.97
Date: Tue, 12 Jun 2018 Prob (F-statistic): 0.00218
Time: 17:05:04 Log-Likelihood: -16.846
No. Observations: 11 AIC: 37.69
Df Residuals: 9 BIC: 38.49
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 3.0009 1.125 2.667 0.026 0.455 5.547
x 0.5000 0.118 4.239 0.002 0.233 0.767
==============================================================================
Omnibus: 1.594 Durbin-Watson: 2.188
Prob(Omnibus): 0.451 Jarque-Bera (JB): 1.108
Skew: -0.567 Prob(JB): 0.575
Kurtosis: 1.936 Cond. No. 29.1
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
III
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.666
Model: OLS Adj. R-squared: 0.629
Method: Least Squares F-statistic: 17.97
Date: Tue, 12 Jun 2018 Prob (F-statistic): 0.00218
Time: 17:05:04 Log-Likelihood: -16.838
No. Observations: 11 AIC: 37.68
Df Residuals: 9 BIC: 38.47
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 3.0025 1.124 2.670 0.026 0.459 5.546
x 0.4997 0.118 4.239 0.002 0.233 0.766
==============================================================================
Omnibus: 19.540 Durbin-Watson: 2.144
Prob(Omnibus): 0.000 Jarque-Bera (JB): 13.478
Skew: 2.041 Prob(JB): 0.00118
Kurtosis: 6.571 Cond. No. 29.1
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
IV
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.667
Model: OLS Adj. R-squared: 0.630
Method: Least Squares F-statistic: 18.00
Date: Tue, 12 Jun 2018 Prob (F-statistic): 0.00216
Time: 17:05:04 Log-Likelihood: -16.833
No. Observations: 11 AIC: 37.67
Df Residuals: 9 BIC: 38.46
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 3.0017 1.124 2.671 0.026 0.459 5.544
x 0.4999 0.118 4.243 0.002 0.233 0.766
==============================================================================
Omnibus: 0.555 Durbin-Watson: 1.662
Prob(Omnibus): 0.758 Jarque-Bera (JB): 0.524
Skew: 0.010 Prob(JB): 0.769
Kurtosis: 1.931 Cond. No. 29.1
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.2. :
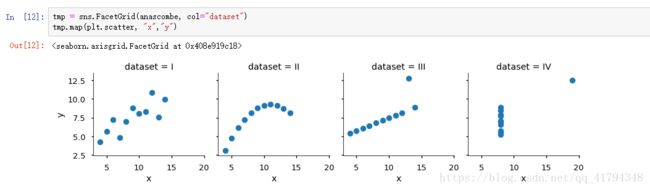
Using Seaborn, visualize all four datasets.
hint: use sns.FacetGrid combined with plt.scatter
好像也没什么解释,调用对应的函数就是了。
notebook 的代码和输出结果如下: