【NOIP2018】DAY1T3——赛道修建（二分答案+贪心策略）

描述
C 城将要举办一系列的赛车比赛。在比赛前，需要在城内修建 ? 条赛道。
C 城一共有 ? 个路口，这些路口编号为 1,2, … , ?，有 ? − 1 条适合于修建赛道的双向通行的道路，每条道路连接着两个路口。其中，第 ? 条道路连接的两个路口编号为 ??和 ??，该道路的长度为 ??。借助这 ? − 1 条道路，从任何一个路口出发都能到达其他所有的路口。
一条赛道是一组互不相同的道路 ?1, ?2, … , ??，满足可以从某个路口出发，依次经过道路 ?1, ?2, … , ??（每条道路经过一次，不允许调头）到达另一个路口。一条赛道的长度等于经过的各道路的长度之和。为保证安全，要求每条道路至多被一条赛道经过。
目前赛道修建的方案尚未确定。你的任务是设计一种赛道修建的方案，使得修建的?条赛道中长度最小的赛道长度最大（即?条赛道中最短赛道的长度尽可能大）。
输入
输入文件第一行包含两个由空格分隔的正整数 ?, ?，分别表示路口数及需要修建的赛道数。
接下来 ? − 1 行，第 ? 行包含三个正整数 ??, ??, ??，表示第 ? 条适合于修建赛道的道路连接的两个路口编号及道路长度。保证任意两个路口均可通过这 ? − 1 条道路相互到达。每行中相邻两数之间均由一个空格分隔。
输出
输出共一行，包含一个整数，表示长度最小的赛道长度的最大值。
样例输入
7 1
1 2 10
1 3 5
2 4 9
2 5 8
3 6 6
3 7 7
样例输出
31
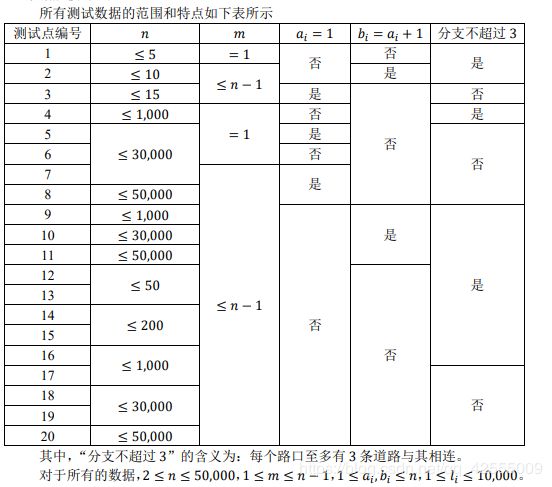
提示
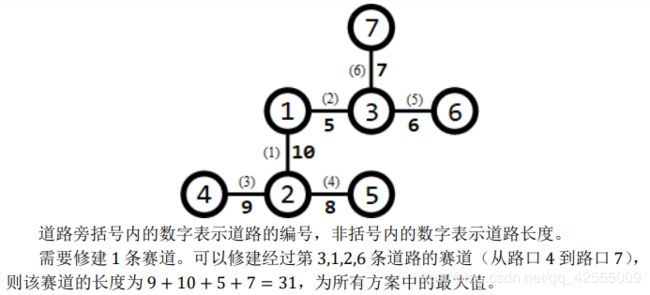
【输入输出样例 1 说明】

据说这是$POI$的原题啊QAQ

其实暴力分给的蛮全的

m=1

直接求树的直径就可以了

$b_i=a_i+1$

那就是一条链了，直接二分直接线性跑就是了

分支不超过3

去掉父亲也就是说二叉树

首先先二分最小的长度

然后考虑对于每一个子树单独考虑

如果只有一个儿子：看距离是否大于二分的值，大于的话赛道数+1，向上返回0，否则返回儿子距离

两个儿子的话就分几种情况讨论

两个的距离都小于二分的值：看两个儿子一起能不能拼出满足的赛道，不行就取最大值

一个大于一个小于：向父亲返回小于的儿子的值

两个大于：赛道数+2，返回0；

$a_i=1$

其实这个想出来的话就基本上可以A了

如果还A不了那我就没法说什么了

所以直接看正解的把

正解

首先第一眼肯定二分

然后。。。$check?$

就像二叉树情况那样，对每个子树分别考虑

那对于每个节点的所有儿子的距离

问题就变成了在保证拼出来的赛道数量最多的情况下使剩下的最大值最大

可以直接双指针做，但$naiive$的我不想打脑壳

于是用$set$维护

于是用multiset存值

贪心策略很简单：枚举最小值，对于每个当前最小值找第一个能和他拼起来的值拼起来

为什么这样是对的呢？

显然如果他能拼起来比他大的也能拼起来，而小的拼肯定能保证剩下那个值最大

上代码

有个比较优秀的优化：二分时以树的直径作为$r$

#include 
using namespace std;
const int N=50004;
inline int read(){
	char ch=getchar();
	int res=0,f=1;
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch))res=(res<<3)+(res<<1)+(ch^48),ch=getchar();
	return res*f;
}
int n,m,adj[N],l,r,nxt[N<<1],to[N<<1],val[N<<1],cnt,dis[N];
inline void addedge(int u,int v,int w){
	nxt[++cnt]=adj[u],adj[u]=cnt,to[cnt]=v,val[cnt]=w;
}
multiset <int> s[N];
multiset <int>::iterator it;
int fpl;
int shx;
int dfs(const int &u,const int &fa){
	s[u].clear();
	for( int e=adj[u];e;e=nxt[e]){
		int v=to[e];if(v==fa)continue;
		int bac=dfs(v,u)+val[e];
		if(bac>=shx)++fpl;
		else s[u].insert(bac);
	}
	int maxn=0;
    while(!s[u].empty()){
        if(s[u].size()==1){
          return max(maxn,*s[u].begin());
        }
        it=s[u].lower_bound(shx-*s[u].begin());
        if(it==s[u].begin()&&s[u].count(*it)==1) it++;
        if(it==s[u].end()){
            maxn=max(maxn,*s[u].begin());
            s[u].erase(s[u].find(*s[u].begin()));
        }
        else {
            fpl++;
            s[u].erase(s[u].find(*it));
            s[u].erase(s[u].find(*s[u].begin()));
        }
    }
    return maxn;
}
inline bool checker(const int &k){
	shx=k;
	fpl=0;dfs(1,0);
	return fpl>=m;
}
inline void solve(){
	int ans=0;
	while(l<=r){
		int mid=(l+r)/2;
		if(checker(mid))l=mid+1,ans=mid;
		else r=mid-1;
	}
	cout<<ans;
}
void suo(int u,int fa){
	for(int e=adj[u];e;e=nxt[e]){
		int v=to[e];
		if(v==fa)continue;dis[v]=dis[u]+val[e];suo(v,u);
	}
}
int main(){
	n=read(),m=read();
	for(int i=1;i<n;++i){
		int u=read(),v=read(),w=read();r+=w;
		addedge(u,v,w),addedge(v,u,w);
	}
	suo(1,0);
	int dw=0,de=0;
	for(int i=1;i<=n;i++){
		if(dis[i]>dw)de=dw,dw=dis[i];
		if(dis[i]<dw&&dis[i]>de)de=dis[i];
	}
	r=de+dw;
	solve();return 0;
}