梯度下降法与优化算法的python实现

梯度下降法与优化算法的python实现

1.SGD(随机梯度下降法)：

每一个参数按照梯度的方向来减小以追求最小化损失函数

目前梯度下降法有三种，它们的区别就是每次更新参数时所需的数据量不一样：批量梯度下降法，小批量梯度下降法，随机梯度下降法

SGD的缺点：

容易收敛到局部最优，但有的时候会被限制在鞍点

class SGD:
def __init__(self, lr=0.01):
    self.lr = lr

def update(self, params, grads):
    for key in params.keys():
        params[key] -= self.lr * grads[key]

2.Momentum：

关于Momentum我们可以简单的这样理解，以高中期间物理学举例：一个小球从山顶滑下，遇到阻碍它的速度就会变小，理想情况下它是滚落到山底，可是大多时候会在山半腰中的一个洼地。

momentum算法思想：参数更新时在一定程度上保留之前更新的方向，同时又利用当前batch的梯度微调最终的更新方向，简言之就是通过积累之前的动量来加速当前的梯度。

Momentum的优点：

积累之前的动量加速当前的梯度

class Momentum:
def __init__(self, lr=0.01, momemtum=0.9):
    self.lr = lr#学习率
    self.momemtum = momemtum#动量因子
    self.v = None#动量

def update(self, params, grads):
    if self.v is None:
        self.v = {}
        for key, val in params.items():
            self.v[key] = np.zeros_like(val)

    for key in params.keys():
        self.v[key] = self.momemtum * self.v[key] - self.lr * grads[key]
        params[key] += self.v[key]

3.Nestrov：

Nestrov同Momentum一样也是一种动量更新方式，但两者不同的是：Nestrov按照之前的动量走一步，再按求导后的梯度再走一步，也就是两者加速当前梯度的方式不同。

它们的优点：在梯度稳定的地方能够加速更新的速度，在梯度不稳定的地方能够稳定梯度。

class Nestrov:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.momentum * self.v[key] - self.lr * grads[key]

4.Adagrad：

Adagrad是一种自适应的优化算法，那么自适应从何体现呢？

它通过每个参数的历史梯度，动态更新每一个参数的学习率，使得每个参数的更新率都能够逐渐减小。前期梯度加大的，学习率减小得更快，梯度小的，学习率减小得更慢些。也就是Adagrad更善于察言观色，根据主体的情况调整自己的状态

AdaGrad有个问题，那就是学习率会不断地衰退。

class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

5.RMSprop：

从上面可以知道AdaGrad的学习率会不断衰减，可能会导致在寻找到全局最优之前就卡死在了局部最优上面！

那么RMSprop的提出就是AdaGrad的一个改版：采用了使用指数衰减平均来慢慢丢弃先前的梯度历史来防止学习率过早地减小。

class RMSprop:
    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

6.Adam：

Adam可以说是一个结合体，结合了动量和自适应，可以对梯度和学习率动态的调整。可以类比从山顶滑下的小球，自适应就相当于给小球的表面凿的凹凸不平，增加它自身的阻力，动量就相当于增加小球的质量，增加了它的惯性。

class Adam:
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)

        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])

            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

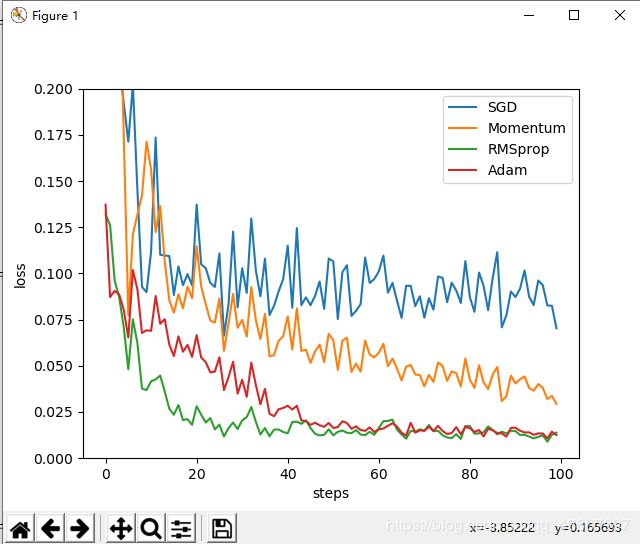
7.利用pytorch可视化：

对比四种不同的优化算法

import torch
import torch.utils.data as Data
import torch.nn.functional as F
from torch.autograd import Variable
import matplotlib.pyplot as plt

LR=0.01
BATCH_SIZE=100
EPOCH=10

x=torch.unsqueeze(torch.linspace(-1,1,1000),dim=1)
y=x.pow(2)+0.2*torch.normal(torch.zeros(*x.size()))

my_dataset=Data.TensorDataset(x,y)
loader=Data.DataLoader(dataset=my_dataset,batch_size=BATCH_SIZE,shuffle=True,)

class Net(torch.nn.Module):
     def __init__(self):
          super(Net,self).__init__()
          self.hidden=torch.nn.Linear(1,20)#输入为n_features个值，输出为n_hidden个神经元
          self.predict=torch.nn.Linear(20,1)#输入为n_hidden个神经元，输出为n_output个输出       
     def forward(self,x):#前向传播过程
          x=torch.relu(self.hidden(x))#将隐藏层输出的x个神经元经过激励函数
          x=self.predict(x)
          return x
SGD=Net()
Momentum=Net()
RMSprop=Net()
Adam=Net()
nets=[SGD,Momentum,RMSprop,Adam]

opt_SGD=torch.optim.SGD(SGD.parameters(),lr=LR)
opt_Momentum=torch.optim.SGD(Momentum.parameters(),lr=LR,momentum=0.8)
opt_RMSprop=torch.optim.RMSprop(RMSprop.parameters(),lr=LR,alpha=0.9)
opt_Adam=torch.optim.Adam(Adam.parameters(),lr=LR,betas=(0.9,0.99))
optimizers=[opt_SGD,opt_Momentum,opt_RMSprop,opt_Adam]

loss_func=torch.nn.MSELoss()
losses_his=[[],[],[],[]]

for epoch in range(EPOCH):
     print(epoch)
     for step,(batch_x,batch_y) in enumerate(loader):
          b_x=Variable(batch_x)
          b_y=Variable(batch_y)
          for net,opt,l_his in zip(nets,optimizers,losses_his):
               output=net(b_x)
               loss=loss_func(output,b_y)
               opt.zero_grad()
               loss.backward()
               opt.step()
               l_his.append(loss.item())

#画出损失值随着训练次数的变化
labels=['SGD','Momentum','RMSprop','Adam']
for i,l_his in enumerate(losses_his):
     plt.plot(l_his,label=labels[i])
plt.legend(loc='best')
plt.xlabel('steps')
plt.ylabel('loss')
plt.ylim((0,0.2))
plt.show()