图卷积神经网络整理
图卷积神经网络的整理
- 一、背景
- 1.1 离散卷积
- 1.2 非结构化数据
- 1.3 图卷积的大致流派
- 二、基于谱的图卷积
- 2.1 傅里叶变换
- 2.2 推广卷积
- 2.3 第一代GCN
- 2.4 第二代GCN
- 2.5 第三代GCN
- 三、基于空间域的图卷积
- 3.1 Graph Attention Network
- 参考
一、背景
1.1 离散卷积
首先这篇文章需要基于你已经理解CNN在图像上的原理及应用。CNN中的卷积本质上就是利用共享参数的一个滤波器,通过计算中心像素以及相邻像素点的加权求和来构成特征图(Feature Map)实现空间特征的提取,卷积核的权重就是网络需要学习的参数。卷积核的参数通过随机初始化再通过反向传播和梯度下降来迭代优化。简单来说,卷积核的参数是通过优化方法求出来的用于提取图像空间域上特征的一个工具,它使得神经网络在将这样的特征输入全连接层或者反卷积层以后能更好地完成分类或者分割的任务。
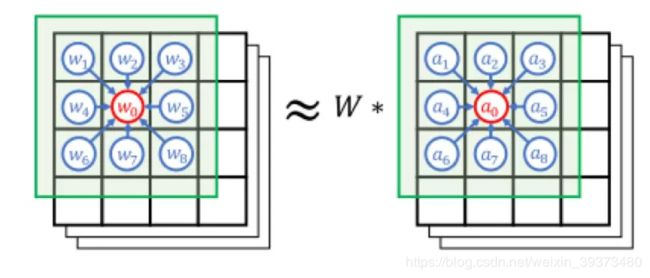
1.2 非结构化数据
以上都是假设在欧几里德空间(欧式空间)中的,欧式空间具有一些很好地性质,这里就不具体讲述了。但是在我们生活中有很多数据是属于非欧式空间的数据,比如说社交网络、知识图谱、3D的蛋白质结构或者点云之类的,我们称这样的数据为图。对于这些数据传统的CNN无法对其进行局部的卷积提取特征,主要是因为这些数据具有非结构化的特点,即每个顶点的邻居结点的个数可能不一样,因此不能用传统的离散卷积去提取特征。
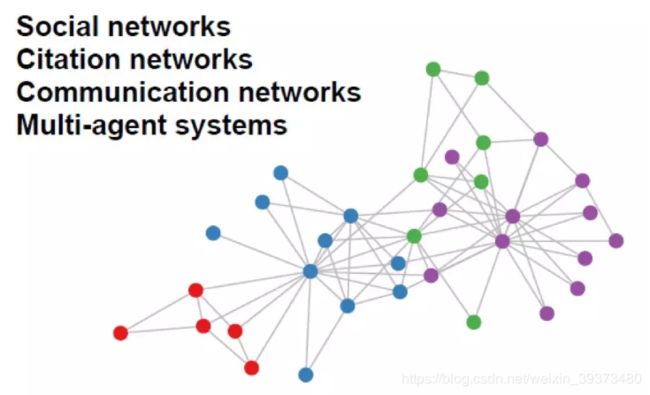
例如下图,如果我只给你所有结点每个结点的特征(可以看做图上的颜色),以及所有结点的邻接矩阵(每两个点之间是否有边),那么我们如何去设计一个网络去做这个图结构的分类(或者是逐点的分割)呢?因此为了完成上述的任务,我们就需要图卷积的应用了。
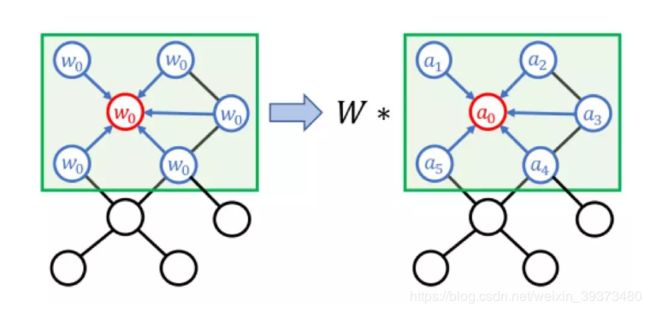
1.3 图卷积的大致流派
在介绍图卷积之前,我们先用数学化的语言介绍一下什么是图。一个图结构其实可以写成如下的表达式: G = ( V , E ) G=(V,E) G=(V,E)其中 V V V是图的结点集合, E E E是图的边集合,设 W W W是图的邻接矩阵, ∣ V ∣ |V| ∣V∣表示结点的个数。 D D D被称为图的度矩阵Degree matraix,其中 D = d i a g ( d 1 , . . . , d N ) D=diag(d1,...,d_N) D=diag(d1,...,dN),其中 d i = ∑ j = 1 N W i j d_i=\sum^N_{j=1}W_{ij} di=∑j=1NWij,即每个结点的邻居的个数。
目前图上的卷积定义基本上可以分为两类,一个是基于谱的图卷积,它们通过傅里叶变换将结点映射到频域空间,通过在频域空间上做乘积来实现时域上的卷积,最后再将做完乘积的特征映射回时域空间,这个在第二节讲。而另一种是基于空间域的图卷积,这就和我们传统的CNN很像了,只不过在图结构上更难定义结点的邻居以及与邻居之间的关系,这些第三节会讲。
二、基于谱的图卷积
2.1 傅里叶变换
傅里叶变换实际上是是将时域上的函数转换为频域上的函数,是一个函数的不同视角: 这个公式的意义就是傅里叶变换是时域信号 f ( t ) f(t) f(t)与基函数 e − i w t e^{-iwt} e−iwt的积分,这个基函数是拉普拉斯算子 Δ \Delta Δ的特征函数。那么什么是拉普拉斯算子呢?拉普拉斯算子就是笛卡尔西坐标系 x i x_i xi中的所有非混合二阶偏导数之和,对于n维笛卡尔坐标系,其表达式为:
这个公式的意义就是傅里叶变换是时域信号 f ( t ) f(t) f(t)与基函数 e − i w t e^{-iwt} e−iwt的积分,这个基函数是拉普拉斯算子 Δ \Delta Δ的特征函数。那么什么是拉普拉斯算子呢?拉普拉斯算子就是笛卡尔西坐标系 x i x_i xi中的所有非混合二阶偏导数之和,对于n维笛卡尔坐标系,其表达式为:

而拉普拉斯算子的特征方程为: Δ g = λ g \Delta g = \lambda g Δg=λg
而 e − i w t e^{-iwt} e−iwt刚好是该特征方程的解,即:

其中特征值 λ = − w 2 \lambda = -w^{2} λ=−w2,也就是说 w w w和特征值 λ \lambda λ密切相关。
因此这里有一个重要的结论:傅里叶变换就是时域信号与拉普帕斯算子特征函数的积分。
那么其实我们可以由整体推特殊,由于离散积分就是一种内积的形式,如果我们可以找到一个graph上的拉普拉斯算子,我们就可以仿上面去定义graph上的傅里叶变换的形式:
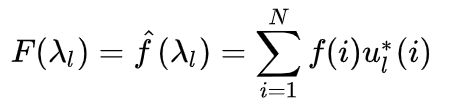
f f f是graph上的 N N N维向量, f ( i ) f(i) f(i)与graph的顶点一一对应, u l l ( i ) u_ll(i) ull(i)表示第 l l l个特征向量的第 i i i个分量。那么特征值 λ l \lambda_l λl下的 f f f的傅里叶变换就是与 λ l \lambda_l λl对应的特征向量 u l l ( i ) u_ll(i) ull(i)的内积运算。
因此对于一个Graph上的拉普拉斯算子,如果它有N个特征值,那么其傅里叶变换可以推广到矩阵形式:

即 f ^ = U T f \hat{f} = U^T f f^=UTf
最后什么是Graph的拉普拉斯算子呢?其实是拉普拉斯矩阵,对于一个图 G = ( V , E ) G=(V,E) G=(V,E),其拉普帕斯矩阵的定义为 L = D − A L=D-A L=D−A,其中 L L L为拉普拉斯矩阵, D D D为顶点的度矩阵(对角矩阵),即对角线上元素以此为各个顶点的度(degree), A A A为图的邻接矩阵。具体的例子可以看下图:

当然这里需要说明,在大部分的GCN中,其使用的拉普拉斯矩阵实际上是Symmetric Normalized Laplacian:
L s y m = D 1 2 L D 1 2 L^{sym} = D^{\frac{1}{2}} LD^{\frac{1}{2}} Lsym=D21LD21
类似地,传统傅里叶变换的逆变换是对 w w w求积分

迁移到graph上就是

类似地也可以写成矩阵的形式:

即 f = U T f ^ f = U^T \hat{f} f=UTf^
2.2 推广卷积
前面其实有提到,基于谱的图卷积通过傅里叶变换将结点映射到频域空间,通过在频域空间上做乘积来实现时域上的卷积,最后再将做完乘积的特征映射回时域空间。这里用到的就是卷积定理,即函数卷积的傅里叶变换是函数傅里叶变换的乘积。
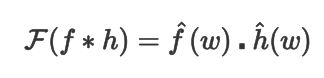
其中 ∗ * ∗为卷积操作,上式可以整理为:
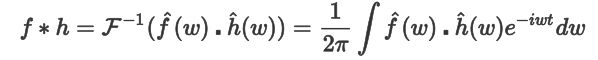
这就是基于谱的图卷积的最初版本,其也可以写成矩阵计算的形式:

即 ( f ∗ h ) G = U ( ( U T f ) ⊙ ( U T h ) ) (f*h)_G = U((U^T f) \odot (U^T h)) (f∗h)G=U((UTf)⊙(UTh))其中 ⊙ \odot ⊙表示对应位置的乘积计算,即内积。
2.3 第一代GCN
Spectral Networks and Locally Connected Networks on Graphs
第一代GCN简单粗暴地把 d i a g ( h ^ ( λ l ) ) diag(\hat{h}(\lambda_l)) diag(h^(λl))变成了卷积核,变成了:

其中 g θ ( Λ ) g_\theta (\Lambda) gθ(Λ)为卷积核, U g θ ( Λ ) U T Ug_\theta (\Lambda)U^T Ugθ(Λ)UT的结果为卷积运算矩阵。

最终的式子可以写成
第一代的参数方法存在一些弊端,主要存在于:
- 计算量大,每次卷积运算都要进行矩阵相乘,计算复杂度 O ( N 3 ) O(N^3) O(N3),即使使用斯坦福的优化算法也是 O ( N 2 . 37 ) O(N^2.37) O(N2.37),且需要特征分解,特征分解的复杂度为 O ( N 3 ) O(N^3) O(N3);
- 没有空间的局部性,每次卷积都要考虑所有的结点;
- 参数个数为 O ( N ) O(N) O(N),传统的CNN的参数个数为常数。
2.4 第二代GCN
Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering
其主要贡献点是将 h ^ ( λ l ) \hat{h}(\lambda_l) h^(λl)改成了 ∑ j = 0 K α j λ l j \sum^K_{j=0}\alpha_j \lambda^j_l ∑j=0Kαjλlj,并且引入了空间局部性。
其中第一点也可以写成

其中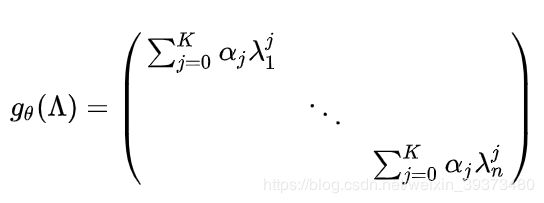
利用矩阵乘法,可以导出:
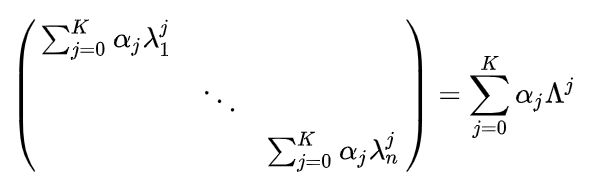
进而
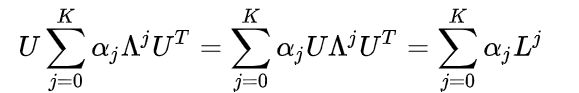
上式成立是利用了特征式分解的性质 L k = U Λ k U T L^k=U\Lambda^k U^T Lk=UΛkUT。最后第二代GCN的公式可以写成:
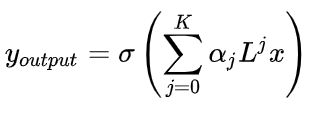
当我们事先把 L k L^k Lk计算好,每一步只需要向量与矩阵相乘,复杂度降低到 O ( K N 2 ) O(KN^2) O(KN2),如果使用稀疏算法,复杂度为 O ( K ∣ E ∣ ) O(K|E|) O(K∣E∣),并且参数个数为常数 K K K。
至于第二点,第二代GCN是如何引入空间局部性的呢?这里首先要讲到拉普拉斯矩阵的性质,对于一个拉普帕斯矩阵,如果 d G ( m , n ) > s d_G(m,n)>s dG(m,n)>s,则 L m , n s = 0 L^s_{m,n}=0 Lm,ns=0,其中 d G ( m , n ) d_G(m,n) dG(m,n)为结点 m m m和结点 n n n的最短距离。因此第二代的卷积公式其实只使用了一个K-hot的邻域,即感受野为 K K K。


另外论文中还提到了一种利用切比雪夫不等式加速的方法:

即利用切比雪夫不等式去逼近卷积核,其中 β k \beta_k βk为切比雪夫多项式的系数。其中 Λ ^ = 2 Λ / λ m a x − I \hat{\Lambda}=2\Lambda/\lambda_{max}-I Λ^=2Λ/λmax−I是为了将其普半径约束到 [ − 1 , 1 ] [-1,1] [−1,1]防止在连乘的过程中爆炸。
根据切比雪夫多项式的性质,可以得到如下递推公式:

不难发现,这个时候原始中不再存在矩阵乘积了,只需要计算矩阵和向量的乘积即可,因此其复杂度是 O ( K ∣ E ∣ ) O(K|E|) O(K∣E∣), E E E为图中边的集合,当graph为稀疏图的时候,计算加速尤为明显。
总结一下第二代GCN:
- 计算复杂度降低到了 O ( K ∣ E ∣ ) O(K|E|) O(K∣E∣);
- 引入了空间局部性。
2.5 第三代GCN
Semi-supervised Classfication with Graph Convolutional Networks
到第二代,基于谱的涂卷机基本成型,第三代GCN改动不大,概括为两个点:
- 令K=1,即每层卷积只考虑直接邻域,类似于CNN中 3 × 3 3\times 3 3×3的卷积核;
- 深度加深,宽度减少(深度学习的经验,深度>宽度)。
对于第二代GCN的公式

我们另 λ m a x = 2 \lambda_{max}=2 λmax=2, k = 1 k=1 k=1,可得:
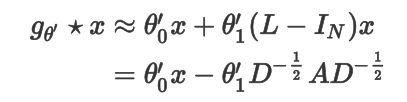
这里运用的是上面提过的归一化后的拉普拉斯矩阵 L = D 1 2 ( D − A ) D 1 2 = I N − D 1 2 A D 1 2 L= D^{\frac{1}{2}} (D-A)D^{\frac{1}{2}}=I_N- D^{\frac{1}{2}} AD^{\frac{1}{2}} L=D21(D−A)D21=IN−D21AD21,其中 A A A为邻接矩阵, D D D为度矩阵。
进一步简化,令 θ 0 ′ = − θ 1 ′ \theta'_0=-\theta'_1 θ0′=−θ1′,可得

由于 I N + D 1 2 A D 1 2 I_N+D^{\frac{1}{2}} AD^{\frac{1}{2}} IN+D21AD21的谱半径范围是[0,2],进一步约束为:
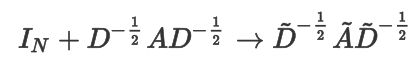
其中 A ^ = A + I N \hat{A} = A +I_N A^=A+IN, D i i = ∑ j A i j ^ D_{ii} = \sum_j \hat{A_{ij}} Dii=∑jAij^
最终通过应用多通道卷积,并表达为矩阵形式,可以得到如下的最终形式:
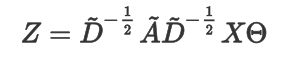
其中 X ∈ R N × C X\in R^{N\times C} X∈RN×C, Θ ∈ R C × F \Theta\in R^{C\times F} Θ∈RC×F, Z ∈ R N × F Z \in R^{N\times F} Z∈RN×F, N , C , F N,C,F N,C,F分别代表节点个数,通道个数和卷积核个数。
总结一下第三代GCN:
- 计算复杂度为 O ( ∣ E ∣ ) O(|E|) O(∣E∣);
- 只考虑1-hot邻域,通过堆叠多层增加感受野。
如果想要自己实现的,可以参考 图卷积网络到底怎么做,这是一份极简的Numpy实现
三、基于空间域的图卷积
3.1 Graph Attention Network
其中最典型的代表作就是 Graph Attention Network,其原理可以看我写的Graph Attention Networks网络结构+代码,以后有时间再补上更多的GCN类型。
参考
https://www.zhihu.com/question/54504471
https://www.jianshu.com/p/f90e7bf2c26e