深度学习-卷积神经网络(python3代码实现)

卷积神经网络（上）

作者：Bossof537
写这个也不容易，小哥哥小姐姐转载请注明出处吧，感谢！

1、简介

卷积神经网络与常规的神经网络十分相似，它们都由可以对权重和偏置进行学习的神经元构成。每个神经元接收一些输入，然后执行点积操作，再紧接一个可选的非线性函数。整个网络仍然表示为单可微分的评估函数，整个网络从一端输入原始图像像素，另一端输出类别的概率。其最后一层（全连接层）同样有损失函数，并且我们学习常规神经网络的方法和技巧在这里仍然奏效。

那么卷积神经网络的不同之处是什么？首先卷积网络很明确地假设所有输入都为图像，这就允许我们在结构中对明确的属性进行编码。这就使得前向函数的实现更加高效，并且极大的减少了网络中参数的数量。

2、结构概述

回顾：正如我们所熟知的，常规神经网络接收一个输入（一维向量），并通过一系列的隐藏层对其进行转换。每个隐藏层由一组神经元构成，其中每个神经元都与前一层的全部神经元相连接，并且同一层的各个神经元都是独立工作的，它们的连接并不共享。位于最后一层的全连接层称为输出层，在分类模型中，它将表示类别的概率。

常规的神经网络并不能很好的应用于完整的图像：在CIFAR-10（一个开源在线的图像数据集）中，图像的尺寸仅为32×32×3（宽度32，高度32，3个通道），因此一个常规神经网络的第一层隐藏层中的单个全连接的神经元将会有32×32×3=3072个权重（全连接网络中，输入向量有多少维，每个神经元就需要有多少个权重，这样才能做点积）。这个数量看起来还好，但是显然这种全连接的结构并不能扩展到更大尺寸的图像。例如：一个200×200×3的大尺寸图像，将会使神经元有200×200×3=120000个权重。并且我们几乎肯定会有好几个这样的神经元，因此参数的数量将会急剧增加。显然，这种全连接结构十分浪费，并且大量的参数将会很快导致过拟合。

三维神经元：卷积神经网络充分利用了输入是由图像组成的这一事实，并以更加合理的方式对结构进行了约束。特别是，与常规网络不同，卷积网络各层的神经元具有三个维度，即宽度、高度、深度。例如：CIFAR-10中作为输入的图像是输入激活量，并且该激活量的大小为32×32×3（分别为宽度，高度，深度）。正如我们即将看到的，每一层的神经元仅与前一层的局部相连，而不是采用全连接的方式。此外，CIFAR-10的最终输出层的尺寸为1×1×10，因为在卷积网络结构的最后我们将会把完整的图像缩减为关于类别概率的一维向量，且该一维向量沿着深度维度排列。如图1所示：

---

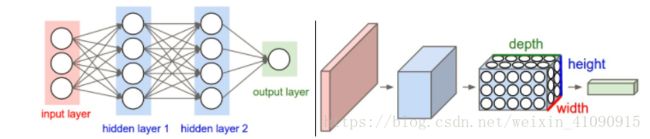
左图：常规三层神经网络。右图：由具有三个维度的神经元构成的卷积网络（宽度，高度，深度）。卷积网络的每一层将三维输入激活量转换为经过神经元激活的三维输出激活量。在这个图例中，红色的输入层代表图像，因此它的宽度和高度就是图像的宽度和高度，而它的深度为3（红，绿，蓝三个通道）

---

3、卷积网络的各层

正如上文所描述的，一个简单的卷积网络由一系列的层所构成，并且卷积网络的每一层通过一个可微函数将一个激活量转换成另一个激活量。我们用三类主要的层来构造卷积网络：卷积层、池化层以及全连接层。我们将通过堆叠这些层来形成一个完整的卷积网络结构。

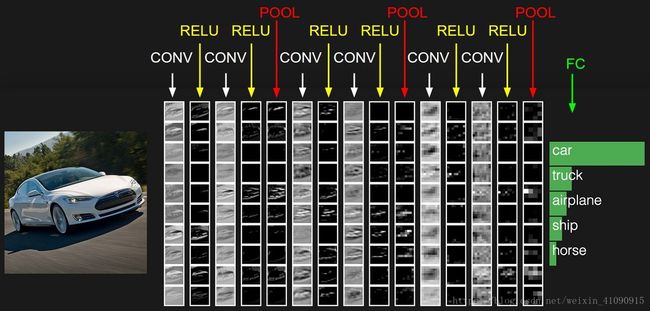
示例：接下来我们将讨论更多细节问题，一个用于对CIFAT-10进行分类的简单的卷积网络的结构是（输入层-卷积层-ReLu函数层-池化层-全连接层），详细来说：

• 输入层（32×32×3）将保存图像的原始像素值，在本例中一个图像具有宽度32，高度32，以及三个颜色通道R，G，B。
• 卷积层负责计算与输入层局部连接的神经元的输出，即分别计算每个神经元的权重与它们所连接的输入激活量的局部之间的点积。如果我们打算使用12个滤波器，那么将会得到大小为32×32×12的激活量。
• ReLu层将会对每一个元素应用一个激活函数，例如以0为阈值的 max(0,x) m a x ( 0 , x ) ，这将使得激活量的尺寸保持不变，仍为32×32×12。
• 池化层将会在二维面上（宽度，高度）执行降采样的操作，得到如16×16×12的激活量。
• 全连接层将会计算类别的概率，得到1×1×10的激活量，其中10个数值分别对应每个类别的概率。全连接层，顾名思义该层和普通的神经网络一样，每一个神经元都将与之前激活量的全部数值相连接。

通过这种方式，卷积网络将原始图像逐层地从原始像素值转换为最终的类别概率。注意，有些层包含一些参数，而有些层则不包含参数。尤其是卷积层和全连接层，其不仅有激活函数，也有参数（神经元的权重和偏置），二者共同对输入激活量执行变换操作。另一方面，ReLu层和池化层将执行一个具有固定功能的函数。卷积层和全连接层中的参数将使用梯度下降进行训练，以使卷积网络计算的类别概率与训练集中每个图像的标签一致。

综上所述：

• 一个卷积网络结构最简单的情况就是顺序排列各个层，以达到将图像激活量转换为输出量激活量的目的。
• 共有几种不同类型的层（例如最流行的：卷积层，全连接层，ReLu层，池化层）。
• 每一层接收一个三维激活量作为输入，并且通过可微函数将其转换为另一个三维激活量作为输出。
• 每一层都可能包含或者不包含参数（例如：卷积层和全连接层有参数，ReLu层和池化层没有参数）。
• 每一层都可能包含或者不包含超参数（例如：卷积层、全连接层、池化层有超参数，ReLu层没有超参数）。

---

---

现在，让我们来对每一层，及其超参数的细节以及其连接方式进行具体的描述。

4、卷积层

卷积层是一个卷积神经网络的核心组成部分，它负责完成大部分计算繁重的工作。

概述以及直观认识：我们先来讨论卷积层是如何进行计算的，并且是从更加直观的角度来进行讨论，而不是将其类比为脑神经。首先，卷积层的参数由一组可以进行学习的滤波器组成。每一个滤波器都是一个小的二维面区域（沿宽度和高度），但却延伸到输入激活量的全部深度。例如：卷积网络第一层上的一个典型滤波器的尺寸可能为5×5×3（即，5个像素的宽度和高度，而3是由于图像的深度为3）。在正向传播期间，我们沿着输入方柱体的宽度和高度方向滑动（更确切地说是卷积）每个滤波器，并计算滤波器的端口与滤波器处于每个位置上的输入的点积。当我们将滤波器沿着输入激活量的高度和宽度滑过之后，将会得到一个二维的激活图，该图给出了滤波器在滑动过的每个位置上得到的结果。直观地说，网络将对滤波器进行学习，当他们看到某种类型的视觉特征时激活，例如第一层上某种方向的条棱或某种颜色的斑点，或者最终在网络的更高层上形成的整个蜂窝或轮状图案。

---

• 举例来说：假设如下图所示，有一个5×5×1的输入激活量，而滤波器的尺寸为3×3×1，该滤波器共有3×3×1=9个端口，其值分别为（-1，0，1，-1，0，1，-1，0，1）。滤波器从输入激活量最左上角的3×3的二维区域位置开始，一次移动一个小格，最终移动到最右下角的位置，滤波器每移动到一个位置，就计算该区域内的输入值与滤波器端口的点积（在本图中，计算1×-1 + 0×0 + 2×1 + 5×-1 + 4×0 + 2×1 + 3×-1 + 4×0 + 5×1 = 0），并将得到的结果放在二维的激活图的相应位置上（在本图中，将点积得到的结果0放在激活图的第一行第二列上）。实际上，这里还需要加上一个偏置。再将最终结果放到二维激活图中。
  

---

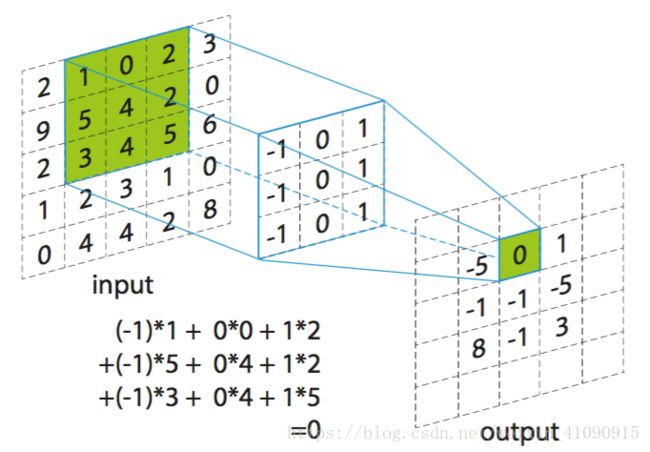
接下来，我们将在每个卷积层上使用一整组的滤波器（即12个滤波器），其中每一个滤波器都将产生一个二维激活图。我们将这些激活图沿着深度堆叠起来，得到一个输出激活量。

从脑神经角度理解：如果您喜欢把它与脑神经进行类比的话，那么三维的输出激活量的每个值也可以解释为神经元的输出值，该神经元只关注于输入的一小部分区域，并且与左右相邻的神经元共享参数（因为这些输出值都是来自同一个滤波器的结果）。接下来我们将讨论这些神经元的连接细节，它们在空间中的排列方式，以及它们的参数共享方案。

局部连接：当处理例如图像这种高维输入时，正如我们上面看到的，将所有神经元进行全连接是不现实的。因此，我们将每个神经元只与输入激活量的部分相连接。这种连接的二维面上的范围是一个超参数，称之为神经元的接收域（相当于是过滤器的大小）。沿着深度方向的连接范围总是和输入激活量的深度相等。必须再次强调我们在处理二维面（宽度和高度）和深度维度上的不对称性。在二维面上是局部连接（沿着宽度和高度的），而沿着输入激活量的整个深度进行的几乎是全连接。

• 例1：例如，假设输入激活量的尺寸是32×32×3。如果接收域（或者说滤波器的尺寸）是5×5，那么卷积层中的每个神经元将会有对应于输入激活量中5×5×3区域的权重，即每个神经元总共有5×5×3=75个权重（加上1个偏置参数）。值得注意的是，沿着深度轴的连接范围必须为3，因为这是输入激活量的深度。
• 例2：假设一个输入激活量的尺寸为16×16×20，接收域的尺寸假设为3×3，卷积层中的每一个神经元与输入方柱体之间将会有3×3×20=180个连接。再次强调，连接在二维面上是局部的（即3×3），但是在输入深度上是全连接的（20）。

---

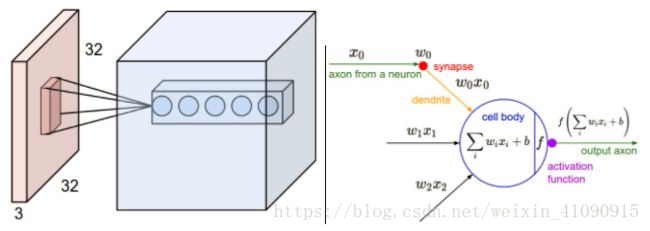
左图：浅红色所表示的是输入激活量（即32×32×3），而深红色表示第一层卷积层上的神经元所连接的局部激活量的示例。卷积层上的每个神经元只与输入激活量的局部相连接，但是在深度上是全连接的。注意，这里沿着深度方向有多个神经元（在本例中是5个），它们都注视着输入激活量的同一区域（参见后文提到的深度列）。右图：仍然计算神经元的权重和输入的点积，再紧接一个非线性函数，只是它们的连接现在被限制在局部区域内。

---

空间排列：我们已经阐明了卷积层中的每个神经元与输入激活量之间的连接，但是我们还没有讨论神经元的个数以及它们如何进行排列的。三个超参数控制着输出激活量的尺寸：分别是深度、步长以及零填充，接下来我们将对这些进行讨论：

1. 首先，输出激活量的深度就是一个超参数：它对应于我们使用的滤波器的个数，每个滤波器都进行学习以从输入中寻找一些不同的东西。例如，第一个卷积层将原始图像作为输入，那么沿着深度维度的不同神经元可以在各种定向条棱或颜色斑点的存在时激活。我们称注视着输入的同一区域的一组神经元为深度列（有些人也喜欢叫纤维条）。
2. 其次，我们必须指定我们滑动滤波器的步长。当步长为1时，我们将滤波器每次移动一个像素。当步长为2（或者3或者更多，虽然实际中并不常见）时，我们将滤波器一次跳跃2个像素来进行滑动。这样将产生二维面（宽度和高度）较小的输出激活量。
3. 正如我们即将看到的，有时在边界周围用0填充输入激活量会很方便。零填充的大小是一个超参数。零填充的优点在于，它可以让我们控制输出激活量的二维面的大小（正如我们马上就要看到的，最常见的是，我们将使用它来精确地保留输入激活量的二维面的大小，以使输入和输出的宽度和高度是相同的）。

我们可以根据输入激活量的大小 (W) ( W ) ，卷积层神经元的接收域的大小 (F) ( F ) ，它们所应用的步长 (S) ( S ) ，以及边界上使用的零填充的大小 (P) ( P ) ，来计算输出激活量的大小。您可以自己证明一下，计算有多少个神经元合适的公式为 (W−F+2P)/S+1 ( W − F + 2 P ) / S + 1 。例如有一个7×7的输入，步长为1的3×3的滤波器，没有零填充即 P=0 P = 0 ，于是我们会得到5×5的输出。如果是2步长我们将会得到3×3的输出。让我们再来看一个图形化的例子：

---

如图所示：在这个例子中，只有一个空间维度（X轴），接收域F=3的神经元，输入大小为W=5，而零填充P=1。左边：神经元以1的步长滑过输入，给出的输出大小为（5 - 3 + 2）/ 1 + 1 = 5。右边：神经元的步长为S=2，给出的输出大小为（5 - 3 + 2）/ 2 + 1 = 3。而本例中的神经元的权重为1，0，-1（最右边的三个绿色方格所示），而偏置为0。这些权重在所有的黄色的神经元之间参数共享（参见下面的参数共享）。

---

零填充的使用：在上面的例子中，左图中的输入大小是5，输出大小也是5。这是因为我们的接收域是3并且我们使用的零填充的大小为1。如果没有使用零填充，那么输出激活量的大小将是3。通常，在步长S = 1时，将零填充设置为P = （F - 1）/2 可以确保输入激活量与输出激活量具有相同大小的二维面（宽度和高度）。以这种方式使用零填充是非常常见的，我们将在讨论更多卷积网络的结构时对其充分原因进行探讨。

步长的限制：需要再次注意，空间排列的超参数是相互约束的。例如，当输入大小 W=10 W = 10 ，不使用零填充即 P=0 P = 0 ，滤波器的大小为 F=3 F = 3 ，那么步长就不可能为2，因为 (W−F+2P)/S+1=(10−3+0)/2+1=4.5 ( W − F + 2 P ) / S + 1 = ( 10 − 3 + 0 ) / 2 + 1 = 4.5 ，即结果为非整数，这显然不行。因此，这样设置超参数是无效的，神经网络库可能会抛出一个异常，或是对其余部分进行零填充，或是对输入进行剪裁，等等。正如我们将在神经网络结构部分看到的，适当调整神经网络的大小以使所有维度得到合理的解决可能是一件非常头疼的事情，因此使用零填充和某些设计准则将显著缓解这种压力。

真实世界的例子： Krizhevsky等人赢得2012年ImageNet挑战赛的架构能够接受大小为227×227×3的图片输入。在第一层卷积层，使用的神经元的接收域大小为 F=11 F = 11 ，步长 S=4 S = 4 ，零填充 P=0 P = 0 。因为 (227−11)/4+1=55 ( 227 − 11 ) / 4 + 1 = 55 ，并且由于卷积层深度 K=96 K = 96 ，因此卷积层的输出大小为55×55×96。55×55×96个神经元中的每一个都与输入激活量的大小为11×11×3的区域连接。此外，每一个深度列（纤维条）上的神经元都与同一个11×11×3的区域相连接，但每个神经元必然都有着不同的权重。

参数共享：参数共享方案在卷积层中用于控制参数的数量。我们使用上述真实世界的例子，在第一层卷积层中共有55×55×96=290400个神经元，并且每一个神经元都有11×11×3=363个权重和一个偏置。将这些加在一起，那么仅在卷积网络的第一层上就有290400×364=105705600个参数。显然，这个数量非常大。事实证明，我们可以通过一个合理的假设来大大减少参数的数量：即一个特征如果在一些位置上（ x,y x , y ）可用于计算，那么在另一个位置上（ x2,y2 x 2 , y 2 ）也可用于计算。换句话说，将一个2维面切片表示为深度切片（例如：大小为55×55×96的激活量具有96个深度切片，每个深度切片大小为55×55）。我们将限制每个深度切片中的神经元具有相同的权重和偏置。有了这种参数共享方案，我们例子中的第一层卷积层中将只有96组不同的权重（每一组对应一个深度切片），总共有96×11×11×3=34848个权重，或者说是34944个参数（加上96个偏置）。或者说，每个深度切片中的55×55个神经元现在将使用相同的参数。在实际的反向传播过程中，激活量中的每个神经元都会计算其权重的梯度，但是这种梯度将叠加在每个深度切片上，并且仅更新每个切片的一组权重。

---

此图为Krizhebsky等人学习到的示例滤波器器，此处显示的96个滤波器中每个滤波器的大小为11×11×3，并且每个滤波器由一个深度切片中的55×55个神经元共享。注意，参数共享假设是相对比较合理的：即如果在图片中的某个位置检测到水平条棱很重要，那么由于图片的平移不变性，它也将在图片的其他位置直观地起到作用。因此不需要重新进行学习来检测卷积层输出激活量中每个55×55不同位置上的水平条棱。

---

请注意，有时参数共享假设可能没有意义。当输入到卷积网络中的图像具有特定的中心结构时，尤其如此，例如，我们期望在图像的一侧学习到完全不同的特征而不是另一侧。一个实际的例子是，当输入的是在图像中居中的人脸图像时，你可能（而且应该）希望在不同的空间位置学习到眼部或头发的特定特征。在这种情况下，通常会放宽参数共享方案，而只将该层称之为局部连接层。

Numpy实际举例：为了使以上的讨论更加具体，我们将同样的思想用具体例子的代码来进行表达。假设输入激活量是一个numpy arrayX，于是：

• 一个在(x,y)位置上的深度列（或者说是纤维条）将是激活量X[x,y,:]。
• 一个深度切片，或者等效于一个在深度d位置上的激活映射图将是激活量X[:,:,d]。

假设输入激活量X的大小为X.shape:(11,11,4)。此外，假设我们使用零填充(即 P=0 P = 0 )，滤波器大小为 F=5 F = 5 ，并且步长为 S=2 S = 2 。因此输出激活量的大小将会是 (11−5)/2+1=4 ( 11 − 5 ) / 2 + 1 = 4 ，即给定一个宽度和高度都为4的激活量。输出激活量中的激活映射图（称之为V）如下所示（在该例中只对一部分元素进行计算）。

• V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
• V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
• V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
• V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

还记得在numpy中*操作表示array之间的每个元素相乘。同时注意到向量W0是神经元的权重向量，b0是神经元的偏置。这里假设W0的大小为W0.shape:(5,5,4)，因为滤波器的大小为5×5，而输入激活量的深度为4。注意，在每个点上，我们都是像之前普通神经网络中那样进行点积，此外，正如我们看到的，我们使用相同的权重和偏置（由于参数共享），并且沿着宽度维度以2为单位递增（即步长）。要构建输出激活量中的第二个激活映射图，我们可以：

• V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
• V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
• V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
• V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
• V[0,1,1] = np.sum(X[:5,2:7,:] * W1) + b1（沿y滑动位置的例子）
• V[2,3,1] = np.sum(X[4:9,6:11,:] * W1) + b1（既沿x又沿y滑动的例子）

正如我们看到的，因为我们正在计算第二个激活映射图，故我们索引到V的第二层深度，并且我们使用了一组不同的参数W1。在上述例子中，我们为了简洁起见，只计算输出激活量 arrayV的一部分。此外，回想一下，这些激活映射图中的每个元素经常都会通过一个诸如ReLu函数之类的激活函数，但是这里并没有提及。

总结：对卷积层进行一下总结。

• 接收一个大小为 W1×H1×D1 W 1 × H 1 × D 1

• 需要四个超参数

  1. 滤波器的数量 K K
  2. 滤波器的大小 F F
  3. 步长 S S
  4. 零填充数量 P P

• 产生一个大小为 W2×H2×D2 W 2 × H 2 × D 2 的激活量，并且

  1. W2=(W1−F+2P)/S+1 W 2 = ( W 1 − F + 2 P ) / S + 1
  2. H2=(H1−F+2P)/S+1 H 2 = ( H 1 − F + 2 P ) / S + 1
  3. D2=K D 2 = K

• 通过参数共享，它将为每个滤波器引入 F⋅F⋅D1 F ⋅ F ⋅ D 1 个权重，总共有 (F⋅F⋅D1)⋅K ( F ⋅ F ⋅ D 1 ) ⋅ K 个权重和 K K 个偏置。

• 在输出激活量中，第 d d 个深度切片（大小为 W2×H2 W 2 × H 2 ）是将第 d d 个滤波器在输入激活量上以步长 S S 进行有效卷积，然后与偏置相加减得到的结果。

一种比较常见的超参数的设置为 F=3,S=1,P=1 F = 3 , S = 1 , P = 1 。

矩阵乘法的实现：注意，卷积运算本质上是将滤波器和输入激活量的局部区域进行点积。而卷积层的常见实现模式是利用这一事实并将卷积层的正向传播制定为如下的一个大矩阵乘法：

1. 输入图像的局部区域在一个通常被称为im2col的操作中被拉伸成列。例如，如果输入激活量的大小为227×227×3并且由大小为11×11×3的滤波器以步长为4进行卷积，那么我们将在输入激活量中拿出11×11×3个像素的区块，并将每个区块拉伸为大小为11×11×3=363的列向量。在输入激活量上以4为步长沿着宽度或者高度滑动都有（227-11）/4+1=55个位置，故在输入激活量上迭代执行拉伸过程，将得到一个大小为363×3025的im2col输出矩阵X_col，其中每列都是一个被拉伸的接收域，因此总共有55×55=3025列。
2. 卷积层的权重类似的拉伸成行。例如，如果有96个大小为11×11×3的滤波器，将会得到一个大小为96×363的矩阵W_row。
3. 卷积的结果现在相当于执行一个大矩阵乘法np.dot(W_row,X_col)，它算出每个滤波器和其在每个位置上的接收域执行点积的结果值，在我们的例子中，该操作的输出矩阵大小为96×3025。
4. 结果必须重新调整为适当的大小，即55×55×96。

这种方法的缺点是浪费内存，因为输入激活量中的一些值在X_col中被复制了多次。然而，其好处是有很多非常有效的矩阵乘法的实现方式可以利用。此外，我们可以重复使用和im2col相同的思想来执行池化操作，我们将在下面的内容中来讨论该操作。

反向传播：卷积操作（对于数据和权重）的反向传播也是卷积（但是，却是具有空间反转的滤波器）。这很容易用一个玩具例子在1维情况下推导出来（现在先不进行扩展）。

1×1卷积：一些论文首先使用1×1卷积作为网络的研究工作。有些人一开始看到1×1卷积会感到有些困惑，尤其是当他们具有信号处理研究背景时。通常情况下，信号是2维的，所以1×1卷积是没有意义的（它只是逐点缩放）。然而，在卷积网络中情况并非如此，因为我们一定要记住，我们是在3维激活量上进行操作，并且滤波器始终是贯穿输入激活量的整个深度。例如，如果输入激活量是32×32×3，于是执行1×1卷积将会高效地执行3维点积（因为输入激活量的深度是3）

扩张卷积：一项最近的研究发展打算向卷积层中再引入一个超参数（参见Fisher Yu 和 Vladlen Koltun的论文），称之为扩张度。到目前为止，我们只讨论了相连续的卷积滤波器。然而，我们也可以设置一个在每个单元格之间有空格的滤波器，称之为扩张。举例来说，假设在1维空间上一个大小为3的滤波器W对输入X进行计算可得：w[0]*x[0] + w[1]*x[1] + w[2]*x[2]，即扩张度为0。若扩张度为1，我们将会计算：w[0]*x[0] + w[1]*x[2] + w[2]*x[4]。换句话说，滤波器的应用具有大小为1的间隔。在某些设置中，将其与0扩张滤波器结合使用，将会非常有用。因为它允许你更加积极地使用更少的图层将输入的空间信息进行合并。例如：如果您将两个3x3 的卷积层叠在一起，那么您可以说服自己，第二层上的神经元是输入激活量的5x5的补丁的函数（我们可以说这些神经元的有效接收域是5×5）。 如果我们使用扩张卷积，那么这个有效的接收域会增长得更快。

5、池化层

我不明白，也不需要明白，做一个傻子好不好………………..
我不想要，也不重要，做一个傻子多么好…………