大话数据结构(二)算法时间复杂度、算法效率的度量方法、算法设计的要求、算法的特性、算法的定义等

     

目录

         算法的定义

算法的特性

输入输出

有穷性

确定性

可行性

算法设计的要求

算法效率的度量方法

事后统计方法

事前统计方法

算法时间复杂度

时间复杂度

O(1)——常数阶

线性阶

对数阶

平方阶

总结

---

下面我们开始第二部分的复习和总结

这一部分主要内容是关于算法的相关概念的讲解，对于从小就接触数学的我们来说算法一定不陌生，只要有一定数学基础的同学都能很容易理解简单算法的核心思想，并在各种编译器上通过各种语言进行实现。

     算法的定义

算法是解决特定问题求解步骤的描述，在计算机中为指令的有限序列，并且每条指令表示一个或多个操作。——《大话数据结构》，就我自身的感悟而言，我认为算法就是一系列指令，每条指令就是一个数学函数，通过这一系列的数学计算，从我们已知的一些数据得到我们想要的数据。

算法的特性

• 输入输出

输入输出：计算机要执行一系列指令需要若干个输入，尽管大部分情况下，算法都需要有输入参数才能得到想要的结果，但是对于某些算法可以不需要输入，比如我们学习编程语言都很熟系的字符串"Hello World"，C语言只需要printf()输出,JAVA可以System.out.print(),C#只需要Console.Writeline()等输出操作就可以了，而不需要输入数据。那么对于输出呢，是的，算法至少需要一个输出，得到我们想要得到的数据，不然就算你这个算法的步骤非常精妙，我们也不需要。

• 有穷性

有穷性：指的是算法在执行有限次步骤后，自动结束，而不会陷入死循环。直白来说就是程序不会无限进行下去，在有限的时间内一定可以完成。然而现实中我们由于各种原因，经常会写出死循环的代码，这就不满足算法的有穷性。

• 确定性

确定性：确定性很好理解，就是我这个算法没一个步骤包括结果都是唯一确定的，都有着自身确定的含义，而不是变色龙一样，不定时的跟随环境的变化而产生二义性。笔者想起曾经在编写C#代码的时候，由于疏忽在两个父类中写了两个一样的变量，由于子类要多继承访问父类的变量，这个时候VS就报错出现二义性的问题，原来是编译器不知道你到底要访问哪个父类的变量，导致了尴尬的错误。举个例子：

class A
{
   public int a; // B1，B2 都将继承一个变量 a
};
class B1 : public A
{
};
class B2 : public A
{
};
class C : public B1, public B2
{
};
 
class program
{
    static void Main(string[] args)
    {
        C c = new C();
        c.a = 10; // ERROR ! 二义性 ！！！
    }
}

• 可行性

可行性：指的是算法的每一步都是可以计算机可以执行的，可行性指的是一个算法可以在计算机上转换成程序运行得到结果。

算法设计的要求

当然，在现实生活中面对同一个问题，不同的人都会有不同的处理方式，在面对同一个数学问题的时候可能也有不同的解法得到正确答案，《大话数据结构》这本书举了一个很有意思的例子，如果要求你写一个1+2+3+······+100的程序，你会怎么写。

大部分同学可能就是一个for循环相加就完事儿了，如下所示

int i,sum=0;
for(i = 0;i <= 100;i++)
{
	sum = sum + i;
}
printf("%d",sum);

但是在18世纪的高斯小朋友就很聪明，它将这100个数分为50对，每对相加等于101，只需要计算50*101=5050就得到结果了

int i,sum = 0,n = 100;
sum = (i + n) * n / 2;
printf("%d",sum);

对比两种算法，第二种算法明显具有更高的效率。

因此一个好的算法应该具有正确性、可读性、健壮性、高效率和存储量的特点，这里只提到了高效率这一点，其他的几点在这里就不多加赘述了。

算法效率的度量方法

• 事后统计方法

事后一支烟，胜过活神仙···。跑题了，但是我们从这个方法的名称上来理解，就能明白这种方法是通过比较两种算法在计算机上运行时间来判断效率的。但是这种方法受到多种因素的制约，显然是有很大缺陷的，可能两个算法在同一台计算机上“跑”的时间“大致”相等，相差个几微秒几毫秒，那如果在未来计算机的运行速度增长为现在的100倍，那这两种算法的差距就非常巨大了。

• 事前统计方法

我们的计算机前辈们，为了对算法的评判更为科学，研究出了一种更为严谨的统计体系——事前统计方法。

事前统计方法：在计算机程序编制前，依据统计方法对算法进行估计。

那么我们现在就通过事前统计方法来对刚才上面提到的例子来进行算法分析。

显然，我们可以看到第一种算法执行了1+（n+1）+n+1=2n+3次

int i,sum=0;//1次
for(i = 0;i <= 100;i++)//n+1次
{
	sum = sum + i;//n次
}
printf("%d",sum);//1次

而第二种算法是1+1+1=3次

int i,sum = 0,n = 100;//1次
sum = (i + n) * n / 2;//1次
printf("%d",sum);//1次

假设每一次执行都需要“相同”的时间，那么第二种算法比第一种活生生的节约了2n次执行的时间，算法的好坏显而易见。

另外，我现在要提出一个例子大家来判断一下，一个算法要执行2n+3次，而另一种要执行3n+1次，大家觉得这两种算法哪种好呢？只要是稍微学习过函数的初中生来回答这个问题都能回答得很好，当然是“不一定”，当n=1时，第一种要比第二种多一次，当n>2时，第一种效率就优于第二种了，并且随着n的增大，这种差异会越来越大。

算法时间复杂度

终于到了这一部分的重点，我们在评判算法的优劣性的过程中经常会用到算法时间复杂度这个概念，那么时间复杂度到底是个什么玩意儿呢。

时间复杂度

（1）时间频度 一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
       （2）时间复杂度 在刚才提到的时间频度中，n称为问题的规模，当n不断变化时，时间频度T(n)也会不断变化。但有时我们想知道它变化时呈现什么规律。为此，我们引入时间复杂度概念。 一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n),使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=Ｏ(f(n)),称Ｏ(f(n)) 为算法的渐进时间复杂度，简称时间复杂度。

另外，上面公式中用到的 Landau符号其实是由德国数论学家保罗·巴赫曼（Paul Bachmann）在其1892年的著作《解析数论》首先引入，由另一位德国数论学家艾德蒙·朗道（Edmund Landau）推广。Landau符号的作用在于用简单的函数来描述复杂函数行为，给出一个上或下（确）界。在计算算法复杂度时一般只用到大O符号，Landau符号体系中的小o符号、Θ符号等等比较不常用。这里的O，最初是用大写希腊字母，但现在都用大写英语字母O；小o符号也是用小写英语字母o，Θ符号则维持大写希腊字母Θ。
        T (n) = Ο(f (n)) 表示存在一个常数C，使得在当n趋于正无穷时总有 T (n) ≤ C * f(n)。简单来说，就是T(n)在n趋于正无穷时最大也就跟f(n)差不多大。也就是说当n趋于正无穷时T (n)的上界是C * f(n)。其虽然对f(n)没有规定，但是一般都是取尽可能简单的函数。例如，O(2n2+n +1) = O (3n2+n+3) = O (7n2 + n) = O ( n2 ) ，一般都只用O(n2)表示就可以了。注意到大O符号里隐藏着一个常数C，所以f(n)里一般不加系数。如果把T(n)当做一棵树，那么O(f(n))所表达的就是树干，只关心其中的主干，其他的细枝末节全都抛弃不管。
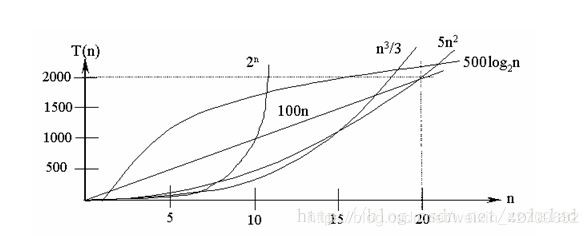
        在各种不同算法中，若算法中语句执行次数为一个常数，则时间复杂度为O(1),另外，在时间频度不相同时，时间复杂度有可能相同，如T(n)=n2+3n+4与T(n)=4n2+2n+1它们的频度不同，但时间复杂度相同，都为O(n2)。 按数量级递增排列，常见的时间复杂度有：常数阶O(1),对数阶O(log2n),线性阶O(n), 线性对数阶O(nlog2n),平方阶O(n2)，立方阶O(n3),...， k次方阶O(nk),指数阶O(2n)。随着问题规模n的不断增大，上述时间复杂度不断增大，算法的执行效率越低。

              

从图中可见，我们应该尽可能选用多项式阶O(nk)的算法，而不希望用指数阶的算法。

      常见的算法时间复杂度由小到大依次为：Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜…＜Ο(2n)＜Ο(n!))

ok，现在我们依次来推导大O阶方法

O(1)——常数阶

int i,sum = 0,n = 100;//1次
sum = (i + n) * n / 2;//1次
printf("%d",sum);//1次

这个算法的运行次数是3次，那么时间复杂度就是O(1)，很多人不理解为什么不是O(3)而是O(1),当然我也不理解···开玩笑的，其实我们可以这么理解，我们现在设定的n是100是吧，那么我现在假定设定的n增加100倍变为10000，我的代码是不是依然是3行，只不过n由100变为了10000。事实上，无论n为多少，上面的代码依然按部就班的执行三次而不会随着n的规模增加而增加，即使算法中有上千条语句，其执行时间也不过是一个较大的常数。更通俗点来说，我们现在可以将n看做一个自变量，我们只关心程序根据n的变化执行时间是否发生变化，不管n变大或者变小，它所在的地方计算机仍然只执行一次。这种执行时间恒定的算法，我们称为具有O(1)的时间复杂度，又叫常数阶。

线性阶

int i,s,a,b
for (i=1;i<=n;i++)//程序根据n的规模的改变而需要改变执行次数
  {    
     s=a+b;　　　 
     b=a;　　　　   
     a=s;  
  } 

上面这段代码，它的循环的时间复杂度为O(n)，因为循环体for中的代码须要执行n次。

对数阶

int i = 1,n = 100;
while(i

我们可以理解为,得到,我们称这种循环的时间复杂度为O[log n]，也称为对数阶。

平方阶

sum=0；               （1次）  
for(i=1;i<=n;i++)     （n次）  
   for(j=1;j<=n;j++)  （n次）  
    sum++；           （n次）  

上面这段代码，它有循环的嵌套，因此执行了次，但是大O阶要求去低阶项，去掉常数项，去掉高阶项的常参得到时间复杂度为O()。

现实中的各种算法的执行次数都是可以通过以上常见的时间复杂度进行运算的，其实在我们日常的算法中，一般O()和O(n)是算法最常见的时间复杂度,而Ο(n!)和O()这种时间复杂度在n较大的时候对计算机来说是一种非常恐怖的存在，很容易引起主机崩溃，因此遇到这种不切实际的算法时间复杂度，我们应该想办法对他们进行"降维打击"，研究效率更高的算法来解决问题。

总结

好了，我们这一部分主要谈到了算法的定义、算法的特性、算法的设计要求、事前统计方法，事后统计方法、执行次数的比较、算法时间复杂度的分析等概念。虽然说当前计算机CPU的运行速度会越来越快，很多算法之间的时间复杂度的“差距”变得很小，甚至观察不到，但是换个角度想，CPU的运行速度变快的同时，时间复杂度更小的算法执行的速度将会是较大的那个的十倍百倍甚至千倍，有时候"负重前行"的固然很好，但是谁都想更想用听着速度更快的、更有创造力的、更聪明的算法吧。

今天周末加班一个人在公司写这个帖子，相信自己坚持写博客和定时提交Git的习惯，也相信自己会在明年的秋招中拿到心仪的offer，借一句话来勉励自己和小伙伴们：大多数人的努力程度,根本还没有到拼智商的地步。 

今天这一部分讲到了算法的相关知识和概念，相信在看了这一部分的朋友会对算法有一个更为清晰的认识。如果觉得文中有什么问题随时欢迎交流指正。