大话数据结构(十)图Graph的相关程序实现

1.图的定义

首先声明一下相关的函数声明`

class Graph
{
public:
	CreateGraph(*G, V, VR);	//按照顶点集合V和边VR的定义构造图G
	DestrotyGraph(*G);	//删除一个图
	LocateVex(G, u);	//若图G中存在顶点u,则返回图中的位置
	GetVex(G, v);	//返回图G中顶点v的值
	PutVex(G, v, value);	//将图G中顶点v赋值value
	FirstAdjVex(G, *v);	//返回顶点v的一个邻接节点，若顶点在G中无邻接节点返回空
	NextAdjVex(G, v, *w);	//返回顶点v相对于顶点w的下一个邻接节点，若w是v的最后一个邻接节点则返回空
	InsertArc(*G, v, w);	//在图中增加弧，若G是无向图，还需要增添对称弧
	DeleteArc(*G, v, w);	//在图G中删除弧,若G是无向图，则还需要删除对称弧
	InsertVex(*G, v);	//在图G中增添新顶点v
	DeleteVex(*G, v);	//删除图G中顶点v以及相关的弧
};

2. 图的五种存储结构

(1).邻接矩阵

图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。

/*构建图结构代码*/
void Graphic::CreateGraph(Graph *G)	//按照顶点集合V和边VR的定义构造图G
{
	int i, j, k,w;
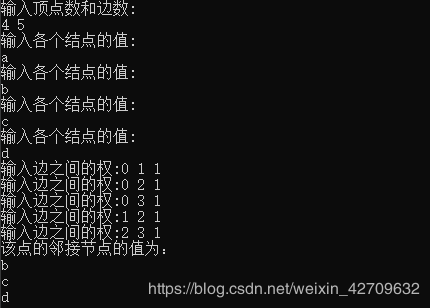
	cout << "输入顶点数和边数:" << endl;
	cin >> G->numVertexes;
	cin>>G->numEdges;
	for (i = 0; i < G->numVertexes; i++)
	{
		cout << "输入各个结点的值:"<<endl;
		cin >> G->vexs[i];
	}
	for (i = 0; i < G->numVertexes; i++)
	{
		for (j = 0; j < G->numVertexes; j++)
		{
			G->arc[i][j] = INFINITY_l;	//邻接矩阵初始化
		}
	}

	for (k = 0; k < G->numEdges; k++)
	{
		cout << "输入边之间的权:";
		cin >> i >> j >> w;
		G->arc[i][j] = w;
		G->arc[j][i] = G->arc[i][j];
		
	}
}

/*若图G中存在顶点u,则返回图中的位置*/
void Graphic::LocateVex(Graph G, VertexType u)const
{
	int MAXSIZE = 1;
	int k = 0;
	int *i = new int[MAXSIZE];
	if (!(&G) || !u)
		throw new exception("输入错误!");
	for(int j=0;j<G.numVertexes;j++)
	{
		if (u == G.vexs[j])
		{
			i[k] = j;
			k++;
			MAXSIZE++;
		}
	}
	for (int j = 0; j < k; j++)
		cout << i[j] << endl;
}

/*返回图G中下标v的值*/
void Graphic::GetVex(Graph G, int v)const
{
	if (!(&G) || !v)
		throw new exception("输入错误!");
	cout<<"输出指定下标存储的字符值:"
	cout << G.vexs[v] << endl;
}

/*将图G中顶点下标v赋值value*/
void Graphic::PutVex(Graph G, int v, char value)const
{
	if (!(&G) || !v || !value)
		throw new exception("输入错误!");
	G.vexs[v] = value;
	return;
}

/*返回顶点下标为v的邻接节点，若顶点在G中无邻接节点返回空*/
void Graphic::FirstAdjVex(Graph G, const int v)const
{
	int j = 0;
	VertexType *VTS = new VertexType[100];	//定义一个邻接节点数组

	for (int i = 0; i < G.numVertexes; i++)
	{
		if (G.arc[i][v] != INFINITY_l)
		{
			VTS[j] = G.vexs[i];	//将邻接节点存入数组中
			j++;
		}
	}
	cout << "该点的邻接节点的值为：\n";
	for (int i = 0; i < j; i++)
	{
		cout << VTS[i] << endl;
	}		
}

输出结果为：

/*返回顶点v相对于顶点w之后的邻接节点，若w是v的最后一个邻接节点则返回空*/
void Graphic::NextAdjVex(Graph G,const int &v,const char &w)
{
	int j = 0;
	VertexType *VTS = new VertexType[100];	//定义一个邻接节点数组
	for (int i = 0; i < G.numVertexes; i++)
	{
		if (G.vexs[i] == w)
			int k = i;
	}
	for (int i = 0; i < G.numVertexes; i++)
	{
		if (G.arc[i][v] != INFINITY_l)
		{
			VTS[j] = G.vexs[i];	//将邻接节点存入数组中
			j++;
		}
	}
	cout << "该点的邻接节点的值为：\n";
	for (int i = 0; i < j; i++)
	{

		if(VTS[i] !=w && i>k)
		{
			cout << VTS[i] << endl;
		}
	}
}

/*在图中增加弧，若G是无向图，还需要增添对称弧*/
void Graphic::InsertArc(Graph *G, const &VertexType v,const &VertexType w,const int &Edge)const
{
	int v_i, w_i;	
	for (int i = 0; i < G->numVertexes; i++)
	{
		if (G->vexs[i] == v)
			int v_i = i;	//存储v的下标
		if (G->vexs[i] == w)
			int w_i = i;	//存储v的下标
	}

	G->arc[v_i][w_i] = Edge;
}

/*在图G中删除弧,若G是无向图，则还需要删除对称弧*/
void Graphic::DeleteArc(Graph *G, const VertexType &v, const VertexType &w)
{
	if (v == nullptr && w == nullptr)
	{
		G->arc[v_i][w_i] = INFINITY_l;
		G->arc[w_i][v_i] = INFINITY_l;
	}
}

/*在图G中增添新顶点v*/
void Graphic::InsertVex(Graph *G, const VertexType &v)
{
	G->numVertexes += 1;
	G->vexs[numVertexes] = v;
}

/*删除图G中顶点v以及相关的弧*/
void Graphic::DeleteVex(Graph *G, const VertexType &v)
{
	for (int i = 0; i < numVertexes; i++)
	{
		if (G->vexs[i] == v)
			int v_i = i;	//返回v的下标
	}

	/*删弧*/
	for (int i = 0; i < numVertexes; i++)
	{
		G->arc[i][v_i] = INFINITY_l;
		G->arc[v_i][i] = INFINITY_l;	//将邻接矩阵相关的元素设为极限值，相当于删掉相关的弧
	}
	/*删点*/
	for (int i = v_i; i < numVertexes; i++)
		G->vexs[i] = G->vex[i+1];	//顶点表中v之后的元素下标前移一位
	numVertexes -= 1;
}

/*删除一个图*/
void Graphic::DestrotyGraph(Graph *G)
{
	delete G;
}

(2).邻接表

邻接矩阵适合结点饱和度较高的图，但是当边相对于顶点较少的时候，这种结构会造成存储空间的大量浪费，用链式的实现存储图结点。
所以把这种数组和链表相结合的存储方式称为邻接表。

/*邻接表结点定义*/
typedef char VertexType;
typedef int EdgeType;
typedef struct 
{
	int adjvex;		//下标
	EdgeType weight;	//权值
	struct EdgeNode *next;	//递归结构
}EdgeNode;//边表结点

typedef struct VertexNode	
{
	VertexType data;	//存储顶点信息
	EdgeNode *firstedge;	//头指针
}AdjList;		//顶点表结点

typedef struct
{
	AdjList adjList[MAXVEX];
	int numVertexes, numEdges;	//当前顶点数和边数
}GraphAdjList;

/*建立图的邻接表结构*/
void CreateALGraph(GraphAdjList *G)
{
	int i, j, k;
	EdgeNode *e;
	cout << "输入顶点数和边数:\n";
	cin >> G->numVertexes >> G->numEdges;
	for (i = 0; i < G->numVertexes; i++)
	{
		cin >> G->adjList[i].data;
		G->adjList[i].firstedge = nullptr;
		for (k = 0; k < G->numEdges; k++)
		{
			cout << "输入边(vi,vj)上的顶点序号：\n";
			cin >> i >> j;
			EdgeNode *e = new EdgeNode;
			e->adjvex = j;
			e->next = G->adjList[i].firstedge;
			G->adjList[i].firstedge = e;
			EdgeNode *e = new EdgeNode;
			e->adjvex = i;
			e->next = G->adjList[j].firstedge;
			G->adjList[j].firstedge = e;
		}
	}
}

(3).十字链表和临接多重表

这两种表是为了优化图的存储结构，将邻接表和逆邻接表结合起来。具体的实现方法不多加赘述。

(4) 边集数组

边集数组是由两个一维数组构成。一个是存储顶点的信息；另一个是存储边的信息，这个边数组每个数据元素由一条边的起点下标begin、终点下标end和权weight组成。