使用余弦退火学习率逃离局部最优点 —— 快照集成(Snapshot Ensembles)在Keras上的应用

先说一下我自己的体会。在了解快照集成（Snapshot Ensembles）之前，老实说我对学习率（Learning Rate）的认识是比较粗浅的。通常我会设置一个比较大的学习率，然后逐渐降低。快照集成这篇论文使用的余弦退火学习率，让我对学习率有了新的认识。这不仅在深度学习的比赛中，而且在实际业务应用中，都具有一定意义。

快照集成是一种在不增加训练成本的前提下，提升模型效果的方法。通常在比赛中更有意义。

原文的代码是Pytorch，本文在Cifar10数据集上，使用Keras框架，证明了快照集成的效果。

本文完整代码（运行时间约25分钟）：
https://github.com/Qiuyan918/Snapshot-Ensembles-Keras-Case-Study/blob/master/Snapshot_Ensemble.ipynb

目录：

• 什么是快照集成（Snapshot Ensembles）？
• 什么是余弦退火学习率（Cosine Annealing Learning Rate）？
• 实验证明

---

1. 什么是快照集成?

快照集成一句话概括就是在同一个训练过程中，将不同节点的，且存在多样性的模型保存下来，再用于集成。这里有两个需要关注的点。

第一点是“同一个训练过程”。不同于一般的集成方法，快照集成不需要重新训练模型，而是在同一个训练过程中，产生成多个模型。我们知道，一个神经网络模型的训练时间很长。如果要训练多个模型，就需要更多时间和算力。快照集成的好处就是在不增加训练成本的前提下，仍然实现集成的效果。

第二点是“存在多样性的模型”。一般的集成方法之所有需要重新训练，就是为了保证模型的多样性，即预测错误的地方是不同的。正因为模型存在多样性，所以集成才能够比单个模型效果更好。而快照集成是如何使得同一训练过程中的模型存在多样性呢？这就需要了解余弦退火这个概念。

---

2. 什么是余弦退火学习率？

图1: 余弦退火学习率

余弦退火学习率是一种在训练过程中，调整学习率的方法。如图1，余弦退火学习率不同于传统的学习率，随着epoch的增加，learning rate 先急速下降，再陡然提升，然后不断重复这个过程。

这样剧烈波动的目的在于：逃离当前的最优点。

图2: 比较传统的由大到小的学习率（左图）和余弦退火学习率（右图）的区别

如上图左，传统的训练过程中学习率逐渐减小，所以模型逐渐找到局部最优点。这个过程中，因为一开始的学习率较大，模型不会踏入陡峭的局部最优点，而是快速往平坦的局部最优点移动。随着学习率逐渐减小，模型最终收敛到一个比较好的最优点。

如上图右，由于余弦退火的学习率急速下降，所以模型会迅速踏入局部最优点（不管是否陡峭），并保存局部最优点的模型。⌈快照集成⌋中⌈快照⌋的指的就是这个意思。保存模型后，学习率重新恢复到一个较大值，逃离当前的局部最优点，并寻找新的最优点。因为不同局部最优点的模型则存到较大的多样性，所以集合之后效果会更好。

两种方式比较起来，可以理解为模型训练的“起点”和“终点”是差不多的。不同的是，余弦退火学习率使得模型的训练过程比较“曲折”。

---

3.1 实验证明

3.1.1 数据

以下的实验将用到的数据是图像数据Cifar10，总共有10种图片类型。

图3: Cifar10

(trainX, trainY), (testX, testY) = cifar10.load_data()

trainX = trainX.astype('float32')
trainX /= 255.0
testX = testX.astype('float32')
testX /= 255.0

idx = 4
plt.imshow(trainX[idx][:,:,0])

我们抽取一张图片看看，见图4。

图4: Cifar10中随机的一张图片

3.1.2 Baseline

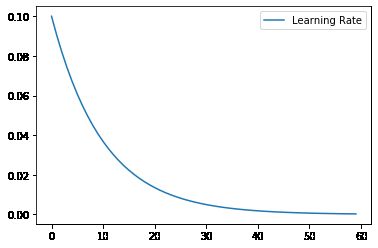图5: 传统的学习率调整过程

首先我们先建立一个baseline模型，来和快照集成的效果进行比较。这里我们定义一个callback来调整学习率，使得它从大到小逐渐降低，如图5。

class LearningRateScheduler(Callback):
  def __init__(self, n_epochs, verbose=0):
    self.epochs = n_epochs
    self.lrates = list()

  def lr_scheduler(self, epoch, n_epochs):
    initial_lrate = 0.1
    lrate = initial_lrate * np.exp(-0.1*epoch)
    return lrate

  def on_epoch_begin(self, epoch, logs={}):
    lr = self.lr_scheduler(epoch, self.epochs)
    print(f'epoch {epoch+1}, lr {lr}')
    K.set_value(self.model.optimizer.lr, lr)
    self.lrates.append(lr)

训练的epoch统一都定位60，batch大小为32。因为是multi-classification的问题，所以loss选用categorical_crossentropy。

%%time
model = my_model()
model.compile('sgd', loss='categorical_crossentropy', metrics=['accuracy'])

batch_size = 32
n_epochs = 60
lrs = LearningRateScheduler(n_epochs)

history = model.fit(trainX, trainY_cat, validation_data=(testX, testY_cat), batch_size = batch_size, epochs=n_epochs,callbacks=[lrs])

Baseline模型的正确率如下：

Train: 0.970, Test: 0.800

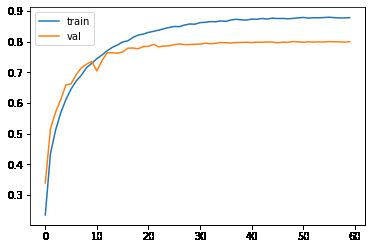图6: baseline模型的学习曲线

如图6，我们可以看到使用传统的方式调整学习率，在epoch 20之后模型的提升非常缓慢。一来是因为学习率减小，二来是因为进入了局部最优点。

3.1.3 Snapshot Ensembles

同样的，我们定义一个余弦退火的callback来调整学习率，并在每一次学习率循环的最低点，保存模型。

# https://machinelearningmastery.com/snapshot-ensemble-deep-learning-neural-network/
class SnapshotEnsemble(Callback):
  def __init__(self, n_epochs, n_cycles, lrate_max, verbose=0):
    self.epochs = n_epochs
    self.cycles = n_cycles
    self.lr_max = lrate_max
    self.lrates = list()

  def cosine_annealing(self, epoch, n_epochs, n_cycles, lrate_max):
    epochs_per_cycle = n_epochs // n_cycles
    cos_inner = (np.pi * (epoch % epochs_per_cycle)) / (epochs_per_cycle)
    return lrate_max/2 * (np.cos(cos_inner) + 1)

  def on_epoch_begin(self, epoch, logs={}):
    lr = self.cosine_annealing(epoch, self.epochs, self.cycles, self.lr_max)
    print(f'epoch {epoch+1}, lr {lr}')
    K.set_value(self.model.optimizer.lr, lr)
    self.lrates.append(lr)

  def on_epoch_end(self, epoch, logs={}):
    epochs_per_cycle = n_epochs // n_cycles
    if epoch != 0 and (epoch + 1) % epochs_per_cycle == 0:
      filename = f"snapshot_model_{int((epoch+1) / epochs_per_cycle)}.h5"
      self.model.save(filename)
      print(f'>saved snapshot {filename}, epoch {epoch}')

epoch和batch_size都和baseline模型保持一致。为了保证每个快照模型能比较充分的训练，每个快照模型训练的epoch为20，所以总共有3次循环，也就是3个模型。

%%time
model2 = my_model()
model2.compile('sgd', loss='categorical_crossentropy', metrics=['accuracy'])

n_epochs = 60
n_cycles = n_epochs / 20
ca = SnapshotEnsemble(n_epochs, n_cycles, 0.1)

hist2 = model2.fit(trainX, trainY_cat, validation_data=(testX, testY_cat), epochs=n_epochs, batch_size = batch_size, callbacks=[ca])

快照集合的正确率如下：

Train: 0.990, Test: 0.814

图7: 快照集合模型的学习曲线

如图7，由于学习率的循环变化，模型的效果也是循环的变化。在达到某个局部最优点后，由于学习率恢复到初始值，模型逃离了当前的最优点，并重新寻找其他局部最优。可以看到快照集合模型的在验证集上的正确率是81.4%，优于baseline的80.0%。

最后，我们将训练过程中3个模型从最后一个依次集合起来。

# evaluate different numbers of ensembles on hold out set
single_scores, ensemble_scores = list(), list()
for i in range(1, len(members)+1):
	# evaluate model with i members
	ensemble_score = evaluate_n_members(members, i, testX, np.argmax(testY_cat, axis=1))
	# evaluate the i'th model standalone
	_, single_score = members[i-1].evaluate(testX, testY_cat, verbose=0)
	# summarize this step
	print('> %d: single=%.3f, ensemble=%.3f' % (i, single_score, ensemble_score))
	ensemble_scores.append(ensemble_score)
	single_scores.append(single_score)
# summarize average accuracy of a single final model
print('Accuracy %.3f (%.3f)' % (np.mean(single_scores), np.std(single_scores)))

集合的效果如下：

> 1: single=0.814, ensemble=0.814
> 2: single=0.806, ensemble=0.816
> 3: single=0.791, ensemble=0.816
Accuracy 0.804 (0.010)

可以看出模型的效果是依次提升的，第3个模型在验证集上的准确性是81.4%，第2个是80.6%，第1个只有79.1%。第3个模型和第2个模型集合使得准确性提升到了81.6%。

综上，

1. 我们看到快照集合的最终模型效果比baseline模型更好，说明baseline可能进入了一个比较差的局部最优点。而使用余弦退火学习率使得模型能够逃离当前的局部最优点，就有可能踏入更好的局部最优点。
2. 快照集合的模型存在多样性，可以提升模型的整体效果，并且不会产生多的训练成本。不过通常这一点对于比赛才有意义，在实际业务应用中应用比较少。但是业务当中可以使用余弦退火学习率，探索多个局部最优点。

如果你有任何疑问或者建议，欢迎留言，或者[email protected]联系我。

参考文献：
[1] Gao Huang and Yixuan Li. Snapshot Ensembles: Train 1, get M for free. arXiv preprint arXiv:1704.00109
[2] https://machinelearningmastery.com/snapshot-ensemble-deep-learning-neural-network/
[3] https://keras.io/examples/cifar10_cnn/