LeetCode刷题笔记(一)
1.Two Sum
Easy
Description
Given an array of integers, return indices of the two numbers such that they add up to a specific target.
You may assume that each input would have exactly one solution, and you may not use the same element twice.
Example
Given nums = [2, 7, 11, 15], target = 9
Because nums[0] + nums[1] = 2 + 7 = 9
return [0, 1]
Code
解题思路:首先,题目要求在数组中找出两个数,使得加和为目标数(target),且找出的数不能重复使用;因此,可建立一个字典(d)用来存储数组中的数及其下标,key = element,value = index;既然数组内两数(nums[i],nums[j])之和为目标数(target),则target - nums[i] = nums[j],所以将问题转化为,在数组中寻找 another_value 使得another_value + nums[i] = target,因此只需判断another_value是否在字典(d)中,并返回another_value的下标即可。
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
d = {} # 建立字典,记录数组元素及其下标,key=element,value=index
for i, value in enumerate(nums): # 循环遍历数组中的数
another_value = target - value # 计算另一个数(another_value)
if another_value in a: # 判断another_value是否在已经加入的字典中,若在则返回,不在则继续遍历
return [d[another_value], i] # 返回两个数的下标,another_value所对应的下标及value所对应的下标(i)
d[value] = i # 运行到这一步说明another_value还未在字典中,因此继续添加元素至字典
return None
时间复杂度为O(n),空间复杂度为O(n)。
2.Add Two Numbers
Medium
Description
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order and each of their nodes contain a single digit. Add the two numbers and return it as a linked list.
You may assume the two numbers do not contain any leading zero(以0开头), except the number 0 itself.
Example
Input: (2 -> 4 -> 3) + (5 -> 6 -> 4)
Output: 7 -> 0 -> 8
Explanation: 342 + 465 = 807.
Code
解题思路:该题目的要求即为两个数从个位开始逐位求和,最终得到两数之和;同时递归遍历链表L1和L2,并将两个链表相同位的数加和,和数对10整除即为需要进位的数(例如8+7 = 15,15//10=1),和数对10求余即为加和后新链表当前位的数(例如8+7 = 15,15%10=5)。
# Definition for singly-linked list.
class ListNode: # 申明链表节点
def __init__(self, x):
self.val = x
self.next = None
class Solution:
def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
initial = ListNode(0) # 初始化链表,随意传一个数进去
node = initial # 另当前节点位初始化的节点
carry = 0 # 初始化进位值为0
while l1 or l2: # 同时遍历l1和l2
x = l1.val if l1 else 0 # 如果l1不为空,则将x赋值为l1的值,否则赋值0
y = l2.val if l2 else 0 # 如果l2不为空,则将y赋值为l2的值,否则赋值0
s = carry + x + y # 求当前位两个数的和并加上上一位得到的进位值
carry = s // 10 # 计算当前位的进位值
node.next = ListNode(s%10) # 求新链表当前位的值,即s对10求余,并令当前节点的next节点为该值的链表节点
node = node.next # 将下一节点变为当前节点,即递归至下一节点
if (l1!=None):l1 = l1.next # 如果l1不为None,递归至l1下一节点
if (l2!=None):l2 = l2.next # 如果l2不为None,递归至l2下一节点
if carry>0: # 当最高为循环计算完成后,判断是否有进位值,若有则需要再增加下一节点
node.next = ListNode(1) # 若有进位值,则需要增加下一节点,并初始化该节点的值为1,因为两个个位数相加不会超过18
return initial.next # 最终返回initial节点之后的节点
时间复杂度为O(n),空间复杂度为O(n)。
3.Longest Substring Without Repeating Characters
Medium
Description
Given a string, find the length of the longest substring without repeating characters.
Example
Example 1
Input: “abcabcbb”
Output: 3
Explanation: The answer is “abc”, with the length of 3.
Example 2
Input: “abcabcbb”
Output: 3
Explanation: The answer is “abc”, with the length of 3.
Example 3
Input: “pwwkew”
Output: 3
Explanation: The answer is “wke”, with the length of 3.
Note that the answer must be a substring, “pwke” is a subsequence and not a substring.
Code
解题思路:记录无重复字串的最大长,首先就是要辨认出各个子串,然后选出最长的子串,解题思路很多,但要保证时间复杂度O(n),也就是需要遍历字符串时动态记录最长子串的起始位置和结束为止,从而更新最大长度值。以下代码的整体思路是,建立一个字典,记录每个字符最新出现的位置的下一个位置,用于遇到相同的字符可以从该字符的下一个位置开始,申明变量i并动态记录最大子串的起始位置,遍历整个字符串时的j就是子串的结尾,申明变量ans动态记录最大子串的长度。
class Solution:
def lengthOfLongestSubstring(self, s):
"""
:type s: str
:rtype: int
"""
st = {} # 建立字典,记录字符串中每个字符最新一次出现的位置
i, ans = 0, 0 # i为最长子串的起始,ans为子串的长度
for j in range(len(s)): # 循环遍历字符串
if s[j] in st: # 如果当前字符(第j个字符)之前未出现过,则子串的起始位置(i)不变;若出现过则i需重新赋值
'''更新子串起始位置,若第j个字符在记录的子串起始位置之前则无需变更,
若在记录的子串起始位置之后则说明第j个字符出现后记录的无重复子串已结束,需重新记录'''
i = max(st[s[j]], i)
ans = max(ans, j - i + 1) # 更新子串的长度,max(之前记录子串长度,当前子串长度为当前位置(j)-起始位置(i)+1)
st[s[j]] = j + 1 # 更新字符的最新位置,+1是为了从下一个字符还是计算
return ans;
时间复杂度为O(n),空间复杂度为O(n)。
4.Median of Two Sorted Arrays
Hard
Description
There are two sorted arrays nums1 and nums2 of size m and n respectively.
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
You may assume nums1 and nums2 cannot be both empty.
Example
Example 1
nums1 = [1, 3]
nums2 = [2]
The median is 2.0
Example 2
nums1 = [1, 2]
nums2 = [3, 4]
The median is (2 + 3)/2 = 2.5
Code
解题思路:首先给定的是两个有序数列,假设数组A和数组B,可以先将两个有序数组随机切分为两半,设A的切分点为i,B的切分点为j,并将两个前半部分的数组放在一起,两个后半部分的数组放在一起,则两个数组就变成左半部分和右半部分,如:
| 左半部分 | 右半部分 |
|---|---|
| A[0],A[1],…A[i-1] | A[i],A[i+1],…A[m-1] |
| B[0],B[1],…B[j-1] | B[j],B[j+1],…B[n-1] |
假设len(A)=m,len(B) = n
此时需要保证:
(1) len(left_part) = len(right_part) (or len(left_part) = len(right_part) + 1)
(2) max(left_part) <= min(right_part)
则: 中位数 = (max(left_part) + min(right_part)) / 2 (or max(left_part))
为了保证以上两个条件,则有:
(a) i + j = m - i + n - j (or i + j = m - i + n - j + 1)
(b) A[i] > B[j-1] and B[j] > A[i-1]
因此问题化简为寻找i以满足条件(a)和(b),又因两数组为有序数组,为了满足时间复杂度O(log(m+n))则使用二分查找。
同时需要注意两点:
(1) n>m,因为在条件(a)中j = (m + n) / 2 - i,若n
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
m, n = len(nums1), len(nums2)
if m > n: # 若m>n则调换两个数组,以防止j为负数
nums1, nums2, m, n = nums2, nums1, n, m
if n == 0: # 若满足此条件说明两个数组均为空
raise ValueError
imin, imax, half_len = 0, m, (m + n + 1) / 2 # 在长度为m的数组中寻找i
while imin <= imax: # 使用二分查找
i = int((imin + imax) / 2)
j = int(half_len - i) # 对应条件(a)
if i < m and nums2[j-1] > nums1[i]: # 如果i太小,则增加i的值
imin = i + 1
elif i > 0 and nums1[i-1] > nums2[j]: # 如果i太大,则减小i的值
imax = i - 1
else: # 执行到这里说明已找到指定的i
'''
如果i为0,说明min(nums1)>=max(nums2),则左半部分的最大值即为nums2[j-1]
如果j为0,说明min(nums2)>=max(nums1),则左半部分的最大值即为nums1[i-1]
若i和j都不为0,则左半部分的最大值,应为max(nums1[i-1], nums2[j-1])
'''
if i == 0: max_of_left = nums2[j-1]
elif j == 0: max_of_left = nums1[i-1]
else: max_of_left = max(nums1[i-1], nums2[j-1])
'''
因之前定义j = (m + n + 1) / 2 - i,所以如果两数组长度之和为奇数时,
左半部分多于有半部分,所以(m + n) % 2 == 1时,直接返回max_of_left
'''
if (m + n) % 2 == 1:
return max_of_left
if i == m: min_of_right = nums2[j]
elif j == n: min_of_right = nums1[i]
else: min_of_right = min(nums1[i], nums2[j])
return (max_of_left + min_of_right) / 2.0
时间复杂度为O(log(m+n)),空间复杂度为O(1)。
以下是大神原版答案:
https://leetcode.com/problems/median-of-two-sorted-arrays/discuss/2481/Share-my-O(log(min(mn))-solution-with-explanation
5.Longest Palindromic(回文) Substring
Medium
Description
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example
Example 1
Input: “babad”
Output: “bab”
Note: “aba” is also a valid answer.
Example 2
Input: “cbbd”
Output: “bb”
Code
解题思路:Palindromic(回文),回文即正向读和反向读一样,例如level、noon、上海自来水来自海上,更多有趣回文例子。介绍两种方法,一个容易理解,但时间复杂度为O(n2),另一个不易理解,但时间复杂度为O(n)。
解法一:遍历字符串,从每一个字符开始同时向两边扩张,寻找左边和右边相同的子串并返回,每返回一个子串皆为一个回文子串,最终返回最大者即可。但是需要注意的是,要分两种情况计算回文子串长度,假设回文子串长度是奇数,即可从当前字符开始向两边寻找,假设回文子串长度是偶数,须从当前字符和下一字符开始寻找,例如“babad”中实际最大回文子串长度为奇数(即3),假设遍历到第一个a时,仅按偶数方法寻找就无法找到“bab”,偶数方法为判断s[1]==s[2],而奇数方法为判断s[1]==s[1],下一次再找时分别向两边移动即s[0]==s[2],即可找到“bab”。因为在整体遍历时,奇数遍历一次,偶数也遍历一次,所以准确的时间复杂度为O(2n2)≈O(n2),空间复杂度为O(3n)≈O(n)。
class Solution:
def longestPalindrome(self, s: str) -> str:
result = '' # 初始化结果值
for i in range(len(s)):
odd_s = self.findlocation(s,i,i) # 假设回文串长度为奇数时,从当前字符开始向两边寻找
even_s = self.findlocation(s,i,i+1) # 假设回文串长度为偶数时,从当前字符和下一字符开始向两边寻找
result = max(odd_s, even_s, result, key=len) # 按照长度更新最大值,max函数中若存在多个一样的最大者,则返回最前者
return result # 返回最大长度回文子串
def findlocation(self,s,l,r):
while l >= 0 and r < len(s) and s[l] == s[r]: # 同时向两边扩张并判断字符是否相同
l -= 1
r += 1
return s[l+1:r] # 当退出循环时,l多减了1,r多加了1,所以在返回字符串时从l+1开始,到r结束即可
时间复杂度为O(n2),空间复杂度为O(n)。
解法二:遍历字符串时,相当于判断在当前字符串情况下,其后增加一个字符,是否会使得最大回文子串增加,当字符串后增加一个字符时,最大回文子串最多增加1个或2个,例如字符串“ab”在末尾增加“a”后最大回文子串长度从2增加至3,字符串“baa”在末尾增加“b”后最大回文子串长度从2增加至4;因此考虑两种情况,一个是增加1的,一个是增加2的,首先初始化最大回文子串长度为1,若增加1的情况,使用动态规划思想,即判断【当前增加的字符位置-最大回文子串长度】的位置的字符至当前增加的字符是否为回文串,如果是,则最大回文子串长度+1,若增加2的情况,即判断【当前增加的字符位置-最大回文子串长度-1】的位置的字符至当前增加的字符是否为回文串,如果是,则最大回文子串长度+2,并为了提高效率可有限考虑+2的情况;其时间复杂度为O(n),空间复杂度O(2n)≈O(n)。
class Solution:
def longestPalindrome(self, s: str) -> str:
if not s:
return ""
start = 0
maxlen = 1 # 初始化最大长度为1,字符串长度为1,则直接返回
for i in range(1,len(s)): # 字符串长度为1直接返回,因此可直接从第二个字符开始遍历
plus2 = s[i-maxlen-1:i+1] # 增加一个字符导致最长回文子串+2
plus1 = s[i-maxlen:i+1] # 增加一个字符导致回文子串+1
if i-maxlen-1>=0 and plus2 == plus2[::-1]:
start = i - maxlen - 1 # 调整其实位置
maxlen += 2 # 更新最大回文子串长度
continue
if i-maxlen>=0 and plus1 == plus1[::-1]:
start = i - maxlen
maxlen += 1
return s[start:start+maxlen] # 按照其实位置和最大回文子串长度返回结果即可
6.ZigZag(Z字形) Conversion
Medium
Description
The string “PAYPALISHIRING” is written in a zigzag pattern on a given number of rows like this: (you may want to display this pattern in a fixed font for better legibility)
P A H N
A P L S I I G
Y I R
And then read line by line: "PAHNAPLSIIGYIR"
Write the code that will take a string and make this conversion given a number of rows:
string convert(string s, int numRows);
Example
Example 1
Input: s = “PAYPALISHIRING”, numRows = 3
Output: “PAHNAPLSIIGYIR”
Explanation:
P A H N
A P L S I I G
Y I R
Example 2
Input: s = “PAYPALISHIRING”, numRows = 4
Output: “PINALSIGYAHRPI”
Explanation:
P I N
A L S I G
Y A H R
P I
Code
解题思路:首先需理解题目意思,即将一个字符串进行“Z”字转换,转换为“Z”字形,并返回按行合并的结果。其次,理清每行字符和前一字符关系即可循环遍历,假设行数为n,首行和末尾行的字符都在纵向排列上,其纵向和纵向之间相隔2n-2个字符,如示例1中首行P和A相差2×3-2=4个字符;中间行纵向字符与斜向字符相隔2(n-1-i)个字符(i为当前行-1),斜向字符与纵向字符相隔2i个字符(i为当前行-1),因此可以按行遍历,添加每行的字符。
class Solution:
def convert(self, s: str, numRows: int) -> str:
ss = '' # 初始化要返回的字符串
lens = len(s) # 提前计算字符串长度,避免后续重复计算
num = numRows-1 # 提前计算,避免后续重复计算
for i in range(numRows): # 遍历行
if numRows == 1: return s # 若给定行为1,则直接返回原字符串
if numRows >= lens:return s # 若给定行号比字符串数量多,则直接返回原字符串
j = i # 第一列字符按行顺序均是原字符顺序
while (i == 0 or i == num) and j < lens: # 首行和末尾行
ss += s[j]
j += 2 * numRows - 2
while (i > 0 and i < num) and j < lens: # 中间行
ss += s[j]
j += 2 * (num - i)
if j >= lens:break # 若j超出字符串长度则退出循环
ss += s[j]
j += 2 * i
return ss
时间复杂度为O(n),空间复杂度为O(n)。
7.Reverse Integer
Easy
Description
Given a 32-bit signed integer, reverse digits of an integer. Assume we are dealing with an environment which could only store integers within the 32-bit signed integer range: [−231, 231 − 1]. For the purpose of this problem, assume that your function returns 0 when the reversed integer overflows.
Example
Example 1
Input: 123
Output: 321
Example 2
Input: -123
Output: -321
Example 3
Input: 120
Output: 21
Code
解题思路:略
class Solution:
def reverse(self, x: int) -> int:
if x == 0: return x
str_x = str(x)
x = ''
if str_x[0] == '-': x += '-'
x += str_x[len(str_x)-1::-1].lstrip('0').rstrip('-')
x = int(x)
if -2**31<x<2**31-1: return x
return 0
时间复杂度为O(n),空间复杂度为O(n)。
8.Palindrome Number
Easy
Description
Determine whether an integer is a palindrome. An integer is a palindrome when it reads the same backward as forward.
Example
Example 1
Input: 121
Output: true
Example 2
Input: -121
Output: false
Explanation: From left to right, it reads -121. From right to left, it becomes 121-. Therefore it is not a palindrome.
Example 3
Input: 10
Output: false
Explanation: Reads 01 from right to left. Therefore it is not a palindrome.
Follow up(进阶):
Coud you solve it without converting the integer to a string?
Code
解题思路:不使用字符串的方式,可以通过求余的方式反向生成新的数,若新的数与原数相同即返回True。进一步,为了减少时间,可以只生成原数的后一半,并判断生成的数与原数的前一半是否相同即可,如何定位只生成原数的后一半,在生成数的同时按位减少(即整除10)原数,若生成的数大于原数,则说明生成的数已超过原数的一半。
总结:把原数的个位数一个一个append到新数的后面,然后比较新书与原数是否相同,比完一半都相同即可。
class Solution:
def isPalindrome(self, x: int) -> bool:
if (x % 10 == 0 or x < 0) and x != 0: return False # 若能整除10但不为0的数和
xx = 0 # 初始化生成数
while x > xx: # 若原数小于生成数,则退出循环
xx = xx * 10 + x % 10 # 生成生成数
x //= 10 # 整除10
return xx == x or xx//10 == x # 如果生成数和原数一样或生成数整除10后和原数相等则位回文数
时间复杂度为O(log10(n)),空间复杂度为O(1)。
9.Regular Expression Matching
Hard
Description
Given an input string (s) and a pattern §, implement regular expression matching with support for ‘.’ and ‘*’.
‘.’ Matches any single character.
‘*’ Matches zero or more of the preceding element.
The matching should cover the entire input string (not partial).
Note:
s could be empty and contains only lowercase letters a-z.
p could be empty and contains only lowercase letters a-z, and characters like . or *.
Example
Example 1
Input:
s = “aa”
p = “a”
Output: false
Explanation: “a” does not match the entire string “aa”.
Example 2
Input:
s = “aa”
p = “a*”
Output: true
Explanation: ‘*’ means zero or more of the precedeng element, ‘a’. Therefore, by repeating ‘a’ once, it becomes “aa”.
Example 3
Input:
s = “ab”
p = “.*”
Output: true
Explanation: “." means "zero or more () of any character (.)”.
Example 4
Input:
s = “aab”
p = “c*a*b"
Output: true
Explanation: c can be repeated 0 times, a can be repeated 1 time. Therefore it matches “aab”.
Example 5
Input:
s = “mississippi”
p = “mis*is*p*.”
Output: false
Code
解题思路:使用动态规划,首先建立len( p)+1行len(s)+1列的表格table,如下表,table[i][j]表示p[:i]和s[:j]的匹配情况;table[0][0]表示匹配p和s都为空的情况;table[1][1]表示匹配p[0]和s[0]。有些地方不是很好描述,但是跟着代码过一遍即可清楚。这里也可直接看大神原答案
0 a a b
0 F F F F
c F F F F
* F F F F
a F F F F
* F F F F
b F F F F
class Solution:
def isMatch(self, s: str, p: str) -> bool:
table = [[False for _ in range(len(s)+1)] for _ in range(len(p)+1)] # 初始化table
table[0][0] = True # 若p和s均为空则返回true
for i in range(2,len(p)+1): # 匹配s为空,p不为空的情况
# 从i=2开始,因为s为空,p的第一个字符不重要,只要第二个是*即可匹配
table[i][0] = table[i-2][0] and p[i-1] == '*'
# 开始逐个字符遍历匹配
for i in range(1,len(p)+1):
for j in range(1,len(s)+1):
if p[i-1] != '*':
# 若当前p不为*,则需要判断上一个字符与上一个正则表达是否匹配成功,同时判断当前字符与当前正则表示是否匹配成功,若都匹配成功即匹配成功
table[i][j] = table[i-1][j-1] and \
(p[i-1] == s[j-1] or p[i-1] == '.')
else:
# 若当前p为*,则分两种情况,一是当前是否匹配成功取决于上一字符或上上字符匹配成功;二是判断当前字符是否与上一正则表达字符匹配成功
table[i][j] = table[i-2][j] or table[i-1][j]
if p[i-2] == s[j-1] or p[i-2] == '.':
table[i][j] |= table[i][j-1]
return table[-1][-1]
时间复杂度为O(mn+n),空间复杂度为O(mn)。
10.Container With Most Water
Medium
Description
Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.
Note: You may not slant the container and n is at least 2.
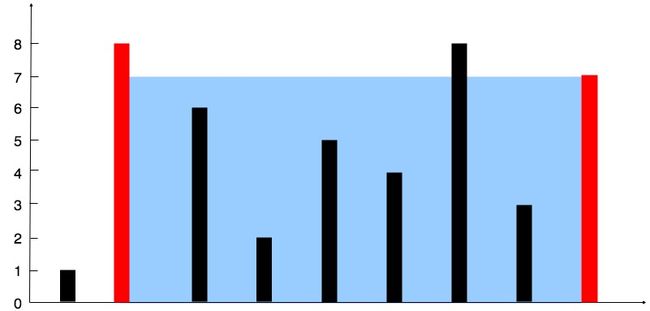
The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.
Example
Example 1
Input: [1,8,6,2,5,4,8,3,7]
Output: 49
Code
解题思路:可以使用逐个遍历的方式计算每两个条形框组成的面积,但显然这种方法时间复杂度太高O(n2),不是我们所期望的。接下来这种方法时间复杂度仅O(n),首先从两边开始,中心思想为若一个条形框的高度低于另一个,则低的向中心移动,高的则不动,因为当前区域为所有边与该低的条形框所组成的区域中面积最大的,再移动高的条形框没有意义。因此只要遍历一遍即可找出最大者。
class Solution:
def maxArea(self, height: List[int]) -> int:
i = 0
j = len(height)-1
s = 0
while j>i:
s = max(s,(j-i) * min(height[i],height[j]))
if height[i] < height[j]:
i += 1
else:
j -= 1
return s
注: 以上代码看着简洁但貌似在速度上可以优化(不过也没必要),即将max和min换成if去判断。
11.Longest Common Prefix
Easy
Description
Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string “”.
Example
Example 1
Input: [“flower”,“flow”,“flight”]
Output: “fl”
Example 2
Input: [“dog”,“racecar”,“car”]
Output: “”
Explanation: There is no common prefix among the input strings.
Note:
All given inputs are in lowercase letters a-z.
Code
解题思路:略。主要是要知道一个python特有的方法,即zip(),zip()可以同时遍历多个可遍历对象,在这里遍历list时加个“*”,可同时将list中各个可遍历对象内的元素遍历出来(可能相对其他语言这有点bug,哈哈)。
当然如果没有zip(*),可以先便利找到最长的字符串,然后根据指针判断也所有字符串也一样
class Solution:
def longestCommonPrefix(self, strs: List[str]) -> str:
if not strs : return ''
for i, x in enumerate(zip(*strs)):
if len(set(x)) > 1:
return strs[0][:i]
return min(strs)
12.3Sum
Medium
Description
Given an array nums of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets(三元组) in the array which gives the sum of zero.
Note:
The solution set must not contain duplicate triplets.
Example
Given array nums = [-1, 0, 1, 2, -1, -4],
A solution set is:
[
[-1, 0, 1],
[-1, -1, 2]
]
Code
解题思路:首先,题目要求在数组中找出三个数,使得三个数的和为0,最笨的办法就是暴力遍历嵌套三个for循环,即时间复杂度为O(n3),这样肯定会超时,换个思路解决;既然需要加和为0,可考虑先将数据排个序,再从两边向中间遍历,容易快速找到加和为0的情况,具体可看代码及注释。
def threeSum(self, nums):
res = [] # 定义一个结果集数组
nums.sort() # 现将数据排序,默认升序,python中的排序使用的是TimSort,时间复杂度为O(nlogn)
for i in range(len(nums)-2):
if i > 0 and nums[i] == nums[i-1]: # 为了避免产生相同的三元组,遇到相同的数时跳过
continue
l, r = i+1, len(nums)-1 # 定位三个数,nums[i]、nums[l]、nums[r],i为当前遍历到的数,l为当前数的下一个数,也是待搜索区域最左侧的数,r为最右侧的数
while l < r:
s = nums[i] + nums[l] + nums[r] # 计算加和
if s < 0: # 若加和小于0,同时nums[r]已为最大值,说明nums[l]偏小,l应该右移
l +=1
elif s > 0: # 若加和大于0,同时nums[l]已为最小值,说明nums[r]偏大,r应该左移
r -= 1
else: # 若加和为0,则可将nums[i], nums[l], nums[r]加入res中
res.append((nums[i], nums[l], nums[r]))
# 因nums[i], nums[l], nums[r]已加入res中,为了避免重复,将跳过相同值
while l < r and nums[l] == nums[l+1]:
l += 1
while l < r and nums[r] == nums[r-1]:
r -= 1
l += 1; r -= 1 # 当前组合加入res后,继续寻找当前i时其他符合加和为0的l和r,因此l和r同时向里收缩一位
return res
排序的时间复杂度为O(nlogn),寻找组合的时间复杂度为小于O(n2),因此总时间复杂度O(nlogn + n2)≈O(n2),空间复杂度为O(n)。
关于TimSort算法,推荐几个链接:先看这个,有图有事例、其次是这个有源码。
13. 3Sum Closest
Medium
Description
Given an array nums of n integers and an integer target, find three integers in nums such that the sum is closest to target. Return the sum of the three integers. You may assume that each input would have exactly one solution.
Example
Given array nums = [-1, 2, 1, -4], and target = 1.
The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).
Code
解题思路:首先,题目要求在数组中找出三个数,使得三个数的和最接近给定的数target,并返回三个数的和。其实该题目的解题思路和上一题差不多,首先,先将数组排序;接着,准备三个指针,第一个i从下标为0的元素开始遍历,至倒数第二个结束,第二个j = i +1,第三个k = len(nums)-1,若三者之和小于target,说明需要增大,则j右移,若三者之和大于target,说明需要减小,则k左移,保证j小于k即可。
class Solution:
def threeSumClosest(self, nums: List[int], target: int) -> int:
nums.sort() # 同样是先排序,时间复杂度为O(nlogn)
diff, s, diff_abs = 0, 0, float('inf') # 初始化差值、返回值和差值的绝对值
for i in range(len(nums)-2):
if i>0 and nums[i] == nums[i-1]: continue # 若有相同值则跳过
j, k = i+1, len(nums) - 1 # j从i的后一位开始向右移,k从最右向左移动
while j < k: # 移动是j小于k则继续
sum_ = nums[i] + nums[j] + nums[k] # 计算三者之和
diff = sum_ - target # 计算差值
if diff == 0: return sum_ # 若差值为0,则直接返回
if abs(diff) < diff_abs: # 若差值的绝对值变小,则更新差值的绝对值与三者之和
diff_abs = abs(diff)
s = sum_
if diff > 0 : k -= 1 # 若差值大于0说明需要减小,则k左移
if diff < 0 : j += 1 # 若差值小于0说明需要增大,则j右移
return s
排序的时间复杂度为O(nlogn),寻找组合的时间复杂度为小于O(n2),因此总时间复杂度O(nlogn + n2)≈O(n2),空间复杂度为O(n)。
14. Letter Combinations of a Phone Number
Medium
Description
Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent.
A mapping of digit to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
Example
Input: “23”
Output: [“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].
Code
解题思路:题目要求通过电话上九宫格键盘输入的数字串,并逐一合并与数字对应的字母。首先建立数字与字母对应的字典,其次循环遍历数字串,并返回字母组合。需要注意的是在最开始建立一个空数组,以便最开始时的计算,详细看代码,分别有两种方式,一个是循环方式,一个好似递归方式。
循环方式:
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
dic = {'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
'6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'} # 建立数字与字母对应的字典
if len(digits) == 0 : return [] # 若数字为空则返回空列表
result = [''] # 初始化结果列表,结果列表用来不断的循环遍历,相当于存储每次计算的结果,再与下一个数字计算时,需拿出一起计算
for digit in digits: # 循环遍历每个数字
current_str = dic[digit] # 获得当前数字对应的字母
current_res = [] # 初始化当前计算的结果集
for letter in current_str: # 循环遍历每个字母
for pre in result: # 循环遍历之前计算好的结果
current_res.append(pre + letter) # 合并
result = current_res # 将本次计算的结果交给result保存
return result
递归方式:
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
dic = {'2': 'abc', '3': 'def', '4': 'ghi', '5': 'jkl',
'6': 'mno', '7': 'pqrs', '8': 'tuv', '9': 'wxyz'}
if len(digits) == 0 : return []
if len(digits) == 1 : return list(dic[digits]) # 递归到只有一个数字时,将数字对应的字母以列表的方式返回,可避免digits仅有一个数字时的问题
current = self.letterCombinations(digits[:-1]) # 最终递归到倒数第二个数字,并返回对应的字符串
back = dic[digits[-1]] # 得到后一个数字的字符串
return [cur + b for cur in current for b in back] # 循环合并
15. 4Sum
Medium
Description
Given an array nums of n integers and an integer target, are there elements a, b, c, and d in nums such that a + b + c + d = target? Find all unique quadruplets in the array which gives the sum of target.
Note:
The solution set must not contain duplicate quadruplets.
Example
Given array nums = [1, 0, -1, 0, -2, 2], and target = 0.
A solution set is:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
Code
解题思路:可参考第12题3sum,只是在最外面再加一层循环,详细可看代码。
循环方式:
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
nums.sort() # 同样先排序
result = [], length = len(nums) # 初始化值
if length == 0: return result # 若给点数据长度为0,则返回空列表
for i in range(length): # 最外层循环
if i>0 and nums[i-1] == nums[i]: continue # 若有相同则跳过
for j in range(i+1,length): # 第二层循环
if j > i+1 and nums[j-1] == nums[j]:continue # 同样有相同跳过,但j必须要在大于i+1时开始,否则出现全是相同值时,无法正确返回结果
m = j + 1, n = len(nums) - 1 # 初始化第二个值和第三个值,其后和3Sum一样
while m < n:
s = nums[i] + nums[j] + nums[m] + nums[n]
if s > target:
n -= 1
elif s < target:
m += 1
else:
result.append([nums[i],nums[j],nums[m],nums[n]])
while m < n and nums[m] == nums[m+1]:
m += 1
while m < n and nums[n] == nums[n-1]:
n -= 1
m += 1; n -= 1
return result
另一种方法:
def fourSum(self, nums, target):
def findNsum(nums, target, N, result, results):
"""
nums:给定数组
target:给定目标值
N:要求加和的数量
result:当前结果
results:最终结果
"""
# 若目标值比数组中最小值的N倍还小、比数组中最大值的N倍还大则无需查找,肯定没有
if len(nums) < N or N < 2 or target < nums[0]*N or target > nums[-1]*N:
return
if N == 2: # 若有要找两个值则方法和上一个一样
l,r = 0,len(nums)-1
while l < r:
s = nums[l] + nums[r]
if s == target:
results.append(result + [nums[l], nums[r]])
l += 1
while l < r and nums[l] == nums[l-1]:
l += 1
elif s < target:
l += 1
else:
r -= 1
else: # 若N!=2,则递归调用
for i in range(len(nums)-N+1): # 因要找出N个数,且后面的值在当前值后开始找,所以仅遍历len(nums)-N个数即可,为保证能遍历len(nums)-N个数,需+1
if i == 0 or (i > 0 and nums[i-1] != nums[i]): # 当前数是第一个数是递归调用,若不是第一个数,则需要避免重复值
findNsum(nums[i+1:], target-nums[i], N-1, result+[nums[i]], results)
results = []
findNsum(sorted(nums), target, 4, [], results)
return results
其实以上两种方法的时间复杂度都是O(n3),但是后者速度更快,目前还不知道为什么。