数据结构与算法基础知识（3）

文章概述

1. 算法时间复杂度的含义;
2. 算法空间复杂度的含义;
   (题外话: 基础内容我们应该了解一下,别人谈论数据结构的时候,我们头脑里应该有个概念。对于这些专业的术语,大脑里最起码要有个概念)

---

算法时间复杂度的含义

a. 算法时间复杂度: 进行算法分析时, 语句的执行次数T(n)是关于问题n的函数,分析T(n)随n的变化情况并且确定T(n)的数量级。算法的时间复杂度,也就是算法的时间量度。记作: T(n)=O(f(n)),表示随着问题规模n的增长,算法执行时间的增长率和f(n)的增长率相同,称为算法的渐近时间复杂度,简称为算法的时间复杂度。其中f(n)是问题规模n的某个函数。(通俗的说,算法的时间复杂度就是算法的执行次数)
一般情况下,随着问题规模n的增大,T(n)增长最慢的算法为最优算法。下面的实例说明执行次数少(T(n)增长的慢)的算法才是我们需求的算法。 实例: 1+2+3+…+100的总和。方案1: 使用for循环执行100次,这时候算法的执行次数为100。方案2: 使用高斯算法,我们只要执行一次。
b. 用大写的O()体现时间复杂度的记法,我们称之为大O记法。
c. 现在,我们分析算法的时间复杂度使用的是大O记法。我们推导大O记法,有下面的几种方式:
(1). 用常数1取代运行时间中的所有加法常数项;
(2). 修改的运行次数函数中,只保留最高阶项;
(3). 如果最高阶项存在且不是1,则去除与这个项相乘的常数。
最后得到的结果就是大O阶。
d. 实例分析下面的大O阶:
(1). `常数阶

int sum=0,n=100;
sum = (n+1)*n/2;
cout<<sum<

程序是一步一步执行的,每一步的执行次数(时间复杂度)是1。总共是3,根据大O记法的推导方式,最后的结果:O(1)。
(2). 线性阶: 一般包括的是非嵌套的循环和一次函数,随着问题规模n的扩大,对应的计算次数呈直线增长。

int n=100,sum=0;
for(int i=0;isum = sum+1;
}

我们将for循环看为一个整体, 第一行代码的执行次数(时间复杂度)是1。整个for循环的执行次数(时间复杂度)是100。根据大O记法的推导方式,最后的结果:O(1)。
(3). 平方阶: 嵌套的两个for循环。

int n=100;
for(int i=0;ifor(int j=0;jcout<<""<

最后结果是: O(n*n)。
(4). 对数阶

int i=1,n=100;
while(i{
  i=i*2;
}

问题主要是判断i有多少次能够达到n。2的x方等于n,则x就是我们需要的结果log2(n)。
通过上面的几个实例,我们可以得出关于循环的时间复杂度: 循环的时间复杂度就是循环体的复杂度乘以循环运行的次数。
这个实例可以验证一下学习成果:

int n=100;
for(int i=0;ifor(int j=i;jcout<<""<

当 i =0; 内循环执行 n次; 当 i=1; 内循环执行n-1次……。最后变成等差数列:
n+n-1+n-2+n-3+…+3+2+1,结果为1/2*(n*n+n),根据大O推导方式最后的结果为O(n*n)。
e. 常见的时间复杂度:

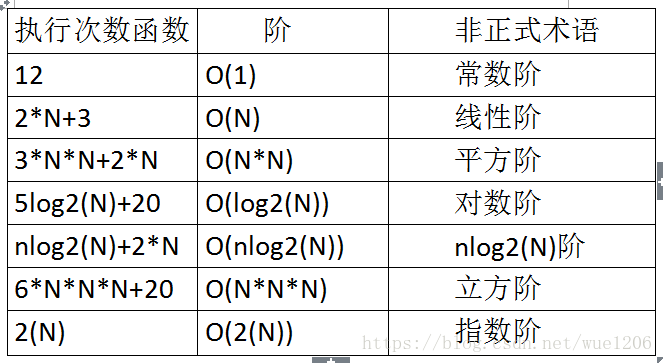
f. 最坏情况与平均情况
最坏情况: 是一种保证, 那就是运行时间不会再坏了。在应用中,这是一种最重要的需求。通常,除非特别指定,我们提到的运行时间都是最坏情况下的运行时间。
平均时间: 是所有情况最有意义的,因为它是期望的运行时间。现实中,运行时间是通过运行一定数量的实验数据后估算出来的。
注意: 一般没有特殊说明的情况下,都是值最坏的运行时间。

---

算法空间复杂度的含义

算法空间复杂度: 通过计算算法所需的存储空间实现,算法空间复杂度的计算公式: S(n) = O(f(n)),其中n为问题的规模,f(n)为语句关于n所占存储空间的函数。
通常,我们所说的时间复杂度指的是运行时间的需求,空间复杂度指的是空间的需求。当不用限定词使用复杂度时,通常指的是时间复杂度(我们主要研究时间复杂度)。