重要性采样在抽样预测领域的应用

引言

抽样预测(Sampling)广泛应用于现代生活的各个领域，比如：总统候选人支持率预估、新药物疗效等等。但是马克吐温说，世界上有三种谎言：“谎言，该死的谎言，统计数据。”这是因为抽样预测是一个精密的多步骤实验，众多抽象概念纵横交错。实施过程中的微小错误或者调整都可能会导致结果大相径庭，甚至推导出与实际情况相悖的结论。本文将就如何构造抽样实验、进行抽样并理解抽样结果进行论述，期望帮助读者掌握抽样预测技术。

抽样预测实验往往非常昂贵，一个样本的抽查成本可能成千上万，如何提高样本利用效率长期困扰着实验者。作者也多次碰到样本数量稀缺的困境，利用重要性采样（Importance sampling）技术，在相同样本数量下预测效果得到了显著的提升，变异系数指标降低了数倍。重要性采样是人工智能领域的重要工具。在强化学习领域，它被用于将行为策略（behavior policy）值转化成目标策略（target policy）值。在NLP领域，Bengio and Sénécal利用它去训练统计语言模型（Statistical language modeling）。虽然重要性采样有坚实的理论基础，并在人工智能领域取得了巨大的成功，但是却很少看到它在其他领域的应用。本文将重点阐述如何将重要性采样技术应用于抽样预测领域。

本文主要贡献包含两块：第一详细阐述了抽样预测流程，并对核心概念进行了直观解释。第二是把重要性采样技术引入到抽样预测领域，同时给出了核心步骤代码实现，并通过模拟数据去验证其理论高效性。据作者所知，这是第一篇公开地将重要性采样应用于抽样预测领域的文章。期望这个研究结果能够帮助广大抽样预测实践者最大限度的摆脱样本稀缺困扰，提升抽样预测效率。

内容组织

文章内容组织分为三大部分，第一部分帮助读者去完整理解抽样预测，第二部分对重要性采样进行详细阐述，最后一部分对传统抽样和重要性采样的效果进行对比。

• 文章第一部分会以简单随机抽样为基础，给出抽样预测实验的基本流程，并对核心步骤进行详细解释。在阐述过程中的核心概念，作者将会尽量使用直观的语言去解释，给出必要的理论证明（只关心实施和应用的读者可以忽略此部分）。对于复杂的核心步骤，还将给出Java代码实现。
• 第二部分首先会给出重要性采样高效性的直观解释，给出必要的理论证明（只关心实施和应用的读者可以忽略此部分）。接下来会重点阐述如何进行分布函数构建、样本抽取以及预测值计算。对于核心步骤，文章会给出Java代码实现以及流程图。
• 最后一部分，作者将构造一份模拟数据，分别采用重要性采样以及传统采样方式进行抽样预测，并对预测效果进行对比。证明重要性采样的高效性。

抽样预测解析

抽样预测的目的是通过从某一群体（母体）中抽取部分个体（样本），通过观测样本的属性值，进而对母体的该属性值进行预测。这个定义里面涉及的的核心概念包括：母体、样本、期望值、个体测量值和预测值。我们将通过下面表格举例进行解释：

例子	母体	样本	期望值	个体测量值	预测值
总统候选人支持率预测	所有选民	抽取的部分选民	候选人真实支持率	某个选民样本是否支持该候选人	该候选人的支持率预测值
产品合格率评估	所有该类型产品	抽取的部分产品	该产品真实合格率	某个产品样本是否合格	产品的预估合格率
国民总收入预估	国家所有人口	抽取的部分人口	国民实际总收入	某个人样本的收入	人均总收入预估值*国家人口总数
某地区家庭汽车总保有量预估	该地区所有家庭	抽取的部分家庭	该地家庭汽车总保有量	某个家庭样本汽车保有量	家庭汽车保有量预测均值*该地区家庭数量

抽样流程及核心概念

简单随机抽样是常见的抽样预测方法，本部分的所有的流程都以简单随机抽样为基础进行讲述。抽样预测的典型实施流程图如下：

具体而言，可以分为四个阶段：

• 确定抽样目标以及母体。
• 抽样
  • 确定样本数量；
  • 样本抽取，即从母体中随机选取所要求数量的样本。
• 预测值计算
  • 对抽取的样本个体进行观测；
  • 对所有的个体测量值进行处理，计算“预测值”。
• 给出实验结果。

这个流程从直觉上讲容易理解。比如想要知道随机抛一枚硬币正面朝上的概率，实施步骤如下：

• 目标期望值：随机抛该硬币，正面朝上的概率。母体：该硬币随机抛无限多次。
• 抽样
  • 确定对该硬币随机抛多少次，比如100次；
  • 实施抛该硬币100次。
• 预测值计算
  • 观测每次抛该硬币，是否正面朝上。
  • 计算正面朝上的比例，比如正面朝上的比例是49%。
• 给出实验结果。比如随机抛该硬币正面朝上的概率是49%。

预测目标

抽样预测实验往往都是为后续的决策提供支持，所以确定预测目标的前提是了解后续的决策需求。

常见的预测目标有两种形式：点预测和区间预测。有时候实验者只需要一个数值结果，而假定精度满足要求。点预测给出一个数值，比如A候选人的支持率为48%。有时候实验者仅仅是把相关满足一定精度的实验结果呈现出来，让第三方去评估和做决策。区间预测采用置信度和置信区间去表示精度。比如在置信度为0.95的条件下，A候选人的支持率的置信区间是48±1%。

从目标类型上讲，抽样预测常常解决两类型问题：比例问题和总量问题。像总统候选人支持率预测、产品合格率评估等都属于比例预测的例子。国民总收入、某地家庭汽车总保有量等属于总量预测的例子。与比例预测相比，总量预测需要得到母体数量，因为预测总量 = 母体数量 * 预测均值。所以，高精度的总量预测实验的前提是获得比较精确的母体总量。例如，要预测国民总收入，必须知道该国的人口总数。

注意！母体数量的获取可能非常复杂，它的获取方式往往并非通过抽样预测方式得到。所以，本文将不会深入讨论这个问题。并且假定，总量预测的实验者已经通过某种方式获得了母体数量。

点预测

人们经常只关心一个数值预测结果，并基于做决策。比如明天下雨的概率是80%，所以先把雨伞放进包里。抛硬币50次之后，抽样预测实验的结论可以是：正面朝上的概率是0.48。这种形式抽样报告结果称为“点预测”。

有人可能会问：这个预测值可信吗。它的可信度的理论基础来自于大数定律，大数定律说：如果重复实施某个实验，那么某个事件发生的频率会趋近于该事件发生概率的期望值。

接下来一个很自然的问题就是，对于一个平衡的硬币，需要抛多少次才能得到真实结果。如果抛1百次、1万次、1亿次，预测值会不会是0.5呢？不幸的是，如下表所示，随着所抛硬币的次数越多，预测值严格等于0.5的概率会越来越小。实际上，如果抛硬币的次数是奇数，那么预测值永远不会等于0.5。

	预测值等于0.5的概率
2次	0.5
10次	0.245
100次	0.08
奇数次	0

置信区间（Confidence interval）

在某种意义上讲，置信区间可以理解为预测误差范围。如果一个预测实验报告为：A候选人的支持率的置信区间是48±1%，那么可以理解其置信区间是47%到49%。

如果置信区间作为结果呈现在预测报告，第三方可以根据置信区间去判断实验的精度。但是在很多时候，控制预测误差本身就是抽样预测实验的目的。置信区间的精度的确定与后续决策相关，比如：

• 需要预测某种试剂的检测准确率，并标示在产品说明书中。如果超过2.5个点的准确率误差会引起大量投诉，那么抽样实验的置信区间范围就必须在5个点以内。
• 需要预测某工业品的合格率，如果已知市场上对合格率一个点敏感。比如每提升一个点，价格就能提升10%。那么合格率抽样预测的置信区间范围应该小于0.5个点。
  在有些情况下，不控制预测误差会导致整个实验失去意义，比如如下结论：
• 某候选人的当选总统的概率是0-1。
• 某个地区家庭汽车均保有量是0-10辆之间。
  这种预测报告没有给出任何有价值的信息。

我们已经接近抽样预测的全貌了，已经明白了：通过大量抽样观测，就能得与期望值在一定误差内的的预测值。但是到底需要多少观测样本呢？

答案非常具有戏剧性：对于某些实验，不做任何抽样就能能得到一定置信区间的预测值。而对于另外一些实验，除非把所有的母体都观测一遍，否则得不到期望置信区间的预测值。为了解决这个困惑，必须要引入置信度的概念。

置信度（Confidence level）

给定期望值的目标置信区间误差范围之后，样本数量真正影响的是置信度。反过来，给定期望值目标置信度之后，样本数量的多少影响着置信区间的误差范围。因为样本数量、置信度和置信区间有着三者相互制约的关系，所以只确定样本数量这一个因素，自然无法唯一确定置信区间误差范围。

有了置信度和置信区间的概念之后，我们就可以给出区间预测结果了。实验报告结论形式可以如下：

• 某城市的人均收入为1w元，该实验的置信度为0.95，其置信区间为0.9w元到1.1w元。
• 某产品的合格率在置信度90%的条件下的置信区间是0.97±0.02。

置信度是一个非常难以理解的概念，很多人把置信度等同于概率。例如对于如下断言：在置信度为0.95的条件下，某种试剂的检测准确率的置信区间是0.92±0.01。有人会把它解释成：该试剂的准确率位于0.92±0.01之间的概率是95%。但是这种理解是错误的。置信度0.95的本质上是说：相同实验重复做100次，每次都会有得到一个预测区间，大概95次的预测区间会包含期望值。而对于单次实验结果，它要么包含期望值，要么不包含期望值，没有任何概率的概念。

总而言之，置信度和置信区间衡量的是抽样预测实验的精度，而不是描述单次抽样实验结果数据的精度。所以实验结果的应该理解为：该数据是通过实施精度为置信度0.95，置信区间误差范围为0.01的实验中得到的。

问题开始变得复杂起来了，样本数量、执行区间和置信度之间究竟是什么样的关系呢？我们将在样本数量确定环节给出。

抽样

抽样分为两个步骤，即：

• 样本数量确定
• 抽取样本

*样本数量确定

大家很容易在网上搜索到一些计算样本数量的工具，那些工具往往只要输入置信度和置信区间范围，就可以自动算出所需样本数量。本小部分下面的内容包含比较多的理论证明，所以对于只关心实施的读者可以忽略本小节后面的内容。

以上讲解告诉我们样本数量会影响置信度和置信区间。要想弄清楚这三者之间的准确的数量关系，就必须要得到预测值和期望值之间的概率分布。遗憾的是，对于大部分抽样实验，我们无法得到。所以我们似乎又走进了死胡同。

它的解决方案是中心极限定理（Central limit theorem），其核心思想是：随着观察样本数量变多，预测值会形成一个以期望值为中心，方差逐渐递减的高斯分布。为了验证这个定理，我们做一个实验，去验证均匀分布的随机变量的和会接近高斯分布。我们从位于0到1之间的均匀分布概率函数U(0,1)中随机抽取1w个点，做成概率直方图显示如下。从图中可以看出，在每个取值点的概率都接近1。

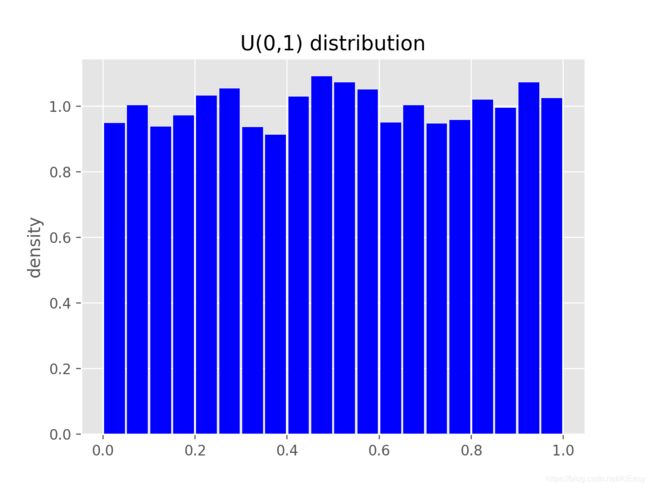
接下来我们考虑来自U(0,1)的10个点的均值变量。我们知道，U(0,1)的期望均值是0.5。按照中心极限定理，10个点均值变量的概率分布会接近以0.5为中心的一个高斯分布。抽样10w个点，对每10个求均值，我们得到1w个均值点，其概率直方图应该会是一个钟形（高斯分布的形状）。其直方图如下，图中红线表示利用中心极限定理计算出来的高斯分布概率曲线。可以看出这两个图的匹配度很高，这个例子验证了中心极限定理的正确性。

具体而言，如果用X表示预测值，μ表示期望值，σ表示期望值的标准差，N表示样本数量。那么中心极限定理断言$$Z=\frac{\left(X-\mu \right)}{\sigma /\sqrt{N}}$$会是一个标准高斯分布的随机变量。

如果期望置信区间误差为ε，这意味着|X-μ|<=ε，置信度为γ，这意味着$$Pr(Z<\sqrt{N}ϵ/\sigma )<\gamma$$。标准高斯分布的分位函数（Quantile function）采用如下符号表示$${\Phi }^{-1}$$，那么抽样数量需要满足如下要求：$$N>={\left({\Phi }^{-1}(\gamma )\sigma /ϵ\right)}^2$$

需要注意的是，我们往往无法预先得到标准差。常见的做法有两种：

• 对于比例预估，可以假定方差为1/4，即最大可能的方差。
• 对于其他分布，需要在抽样结果出来之后计算进行预测。

对于上面的第二种情况，由于方差预先得不到，所以样本数量可能一次性无法确定。所以，样本数量可能在完成初次观察之后继续增加。

另一个需要注意的点是，实施抽样实验的过程中，经常会出现无效样本。所以为了满足实验精度要求，实际抽样数量应该大于如上理论计算值。

样本抽取

在抽取样本过程中，最重要的是要保证随机性。否则，实验结果的有效性将无法得到保证。2016年美国大选主流媒体预测基本上都错了，一个重要的原因就是抽样调查的随机性没有得到保证。
假定母体数量为T，个体的构成一个IDS序列，为了从中随机抽取sampleSize个样本。抽取流程图如下：

具体而言分为三个步骤：

• 构建T个插槽，每个个体id放入到一个插槽里。
• 每次随机抽取一个插槽，插槽内id对应个体即为选中样本。
• 重复第二步，一直到抽取完sampleSize个样本。

代码实现一般是获取一个0到1之间的随机数，将该随机数乘上母体数量T，向下取整得到抽中个体id。需要注意的是，可能会重复抽取到同一个体id，所以需要抽中id进行排重。下面是代码实现：

public static Long[] sampling(Long[] ids, int sampleSize)
    {
        Random random = new Random();
        Set<Long> sampleIds = new HashSet<Long>();
        int idSize = ids.length;

        while(sampleIds.size() < sampleSize)
        {
            double rdVal = random.nextDouble();
            int index = (int)(rdVal*idSize);
            sampleIds.add(ids[index]);
        }

        return sampleIds.toArray(new Long[sampleIds.size()]);
    }

预测值计算

• 如果是点预测的话，预测值往往就是对个体测量值进行简单加和求平均。
• 如果是区间预测，预测均值需要加上预测误差，给出置信度和置信区间。

重要性采样（Importance sampling）

正如其名，简单随机抽样的实施简单，基于中心极限定理还能给出严谨的置信度和置信区间精度。在没有任何先验知识的前提下，那么简单随机抽样几乎是最好的选择。

但是，在在很多场景下，我们面对的现实是：

• 抽样成本太高。在可接受的成本范围内，通过简单随机抽样实验的置信度和置信区间都不可接受。
• 积累了大量的先验知识，知道某些样本的潜在取值。

我们就需要找到一种更高效利用样本的抽样方法，重要性采样可以充分利用先验知识去提高样本效率。
重要性采样的核心思想是，如果能够预先知道个体的潜在观测值（先验知识），那么应该给予潜在观测值高的个体更高的抽样概率。下面通过一些例子给出一些直观认识。

• 如果抽样预估美国人的家庭资产总值，那么像比尔盖茨、贝索斯这些顶级富豪就必须要被计算，而次级富豪被抽中的概率也应该远高于贫困家庭被抽中的概率。如果没有抽中比尔盖茨，这意味着，美国家庭资产平均数可能要少几千美元。而如果错过一个流浪汉，影响几乎可以忽略。
• 如果要预测一种女性化妆品的上市销量，调查对象显然应该主要面向女性。
• 要预测白酒的上市销量，调查对象就应该主要面向成年男性。

如果先验知道某些个体对预测值没有影响，那么这部分个体可以直接不抽样。

• 例如想要调查野生大熊猫的总数量，要选10个地方做调查。显然主要的精力应该在四川，东北就可以不去了。

具备了基本的直观认识之后，接下来我们来验证一下重要性采样的理论基础。对于只关心实施的读者可以忽略理论证明部分。

*理论证明

假定要得到概率分布为p(x)的均值，其解析解应该是$$\int xp(x)dx$$。抽样预测的本质就是按照概率分布p(x)去抽取样本，计算其均值。假定抽取了N个样本，分别为x1…xN，预测值计算公式为$$1/N\sum _{i=1}^{N}xi$$。求解均值的本质是积分，很容易看出如下等式成立$$\int xp(x)dx=\int x\frac{p(x)}{q(x)}\ast q(x)dx$$。重要性采样的就是要寻找建议分布（proposal distribution）q(x)，然后按照q(x)概率进行抽样，同样抽取了N个样本，分别为x1…xN，预测值的计算公式应该为$$1/N\sum _{i=1}^{N}xi\ast \frac{p(xi)}{q(xi)}$$。

理论上讲，如果抽取样本数量N无限大，那么以上两种方法所得到的结果都会收敛到期望值。但是当样本数量比较小的时候，抽样预测的准确度取决于方差的大小。重要性采样的目的就是找到建议分布q(x)，使xp(x)/q(x)的值保持稳定，减少预测方差。

在大量实际抽样实验里面，实际分布p(x)等于1除以母体总数量，所以要让xp(x)/q(x)保持稳定，等同于让x/q(x)保持稳定。这就意味着x值大的时候，q(x)应该大，x值小的时候，q(x)应该小。这就解释了我们的直观认识，应该给予观测值高的个体更高的抽样概率。举例来说，如果要抽样预估美国人的家庭资产总值，那么像比尔盖茨、贝索斯这些顶级富豪就必须要被计算。

建议分布构建

重要性采用实施的第一步就是构建一个合理的建议分布，它的本质就是给每个个体一个预估值，这个预估值体现了该个体的抽样概率q(x)。我们真正关心的是个体之间的倍数关系，所以在进行个体值预估的时候，不需要满足预估值之和等于1的概率分布约束。概率归一化计算可以在预测值计算环节进行后续处理。但是在进行抽样实验之前，当然无法得知每个个体的实际取值x。实际上如果q(x)严格按照x的大小进行抽取，那么只要抽取一个样本就能准确得到期望值。

在实践过程中，可以通过其他手段，获得合理的个体近似值。典型的方法有如下：

• 对母体的所有样本进行分组，对每组之间的大小关系进行预估。比如：想要知道一个国家人均总收入，需要进行全国抽样。但是，不同地域间的差异是预先可知，哪么富裕地区的个人抽样概率就应该高于贫困地区的。
• 利用之前实验的结果或其他关联数据。比如：一种抽样实验已经做了很多次，那么之前积累的数据可以作为本次实验的先验知识。又比如：想要得到某个地区的家庭汽车保有量，如果手头有家庭收入数据，那么家庭收入数就可以作为建议分布的先验知识。
• 专家访谈，或者进行分析推导。比如：想对某种药物的有效性进行抽样验证。需要对不同年龄段、不同性别的病人进行抽样。抽样比例可以听取专家的意见，也可以对药品以及人体结构进行分析得到一些先验知识。

健壮性分析

由于建议分布的构建是经验性操作，不同实验者构建的建议分布不会完全相同。一个自然的问题就是重要性分布预测值对建议分布的敏感度如何，也就是如果建议分布的微小变化是否会导致预测值的巨大变化？这个答案是否定的。

对于健壮性，这里做一点定性的分析。假定理想建议分布为R（x取值与q(x)绝对成正比），随机抽取分布为U，假定用N表示U和R之间的扭曲程度。那么在R和U之间的建议分布的预测值都应该比U的更精确。如果q(x)沿着R往与U相反的方向扭曲，只要扭曲程度小于N，重要性采样的预测值也应该更加精确。所以建议分布的健壮性给予了实验者足够建议空间。

在本文后面模拟验证部分，我们将构建不同的建议分布，去验证建议分布的健壮性。

预测目标

根据以上讨论，重要性采样的精度的提升主要来自于利用先验知识降低方差。先验知识的有效性以及其概率分布都会影响置信度和置信区间。但是在大部分情况下，很难构建先验知识与预测值的联合概率分布，这就使得无法获得比较精确的置信度、置信区间。所以采用重要性采样，如果只是进行单次实验，我们往往只能进行点预测。

有时候，实验者能够重复实施抽样预测实验，如果假定实验数据分布变化不大，那么多次抽样结果的均值符合大数定律。所以在进行多次实验之后，我们可以计算实验的置信度和置信区间。此外，通过多次实验，我们还能得到变异系数指标，它是多次实验预测值的标准差与均值的比值。这是一个非常检验抽样有效性的指标。毕竟在现实生活中，大部分事物的变化都是缓慢的朝着某个方向发展的，联系抽样的结果之间的差别不应该出现太大的差别。

抽样

样本数量确定

重要性采样样本数量确定有两种主要的方式：

• 采用简单随机抽样方式来确定。如此以来，如果假定先验知识有效，那么简单随机抽样的误差就是重要性采样误差的上线。换而言之，保持置信区间不变，重要性采样的置信度会更高，如果保持置信度不变，置信区间会更小。
• 其他因素决定，比如成本因素，时间因素等等。在这种情况下，与采用简单随机抽样相比，实验者采用了更有效的采样方式。

样本抽取

重要性采样的样本抽取的核心工作是构建建议分布q(x)，然后从q(x)中进行随机抽取。假定要抽取sampleSize个样本，抽样流程图如下：

具体步骤如下：

1. 母体中所有个体的id进行一个随机排序，构建id序列，命名为IDs，此后顺序不变。比如id1、id2、id3…

2. 基于该IDs序列，构建先验值序列，命名为VALUEs。比如2、3、1…

3. 基于该IDs序列，对截止并包含当前id值对应的先验值进行求和，构建累计分布函数值序列，命名为CDFs。并记录下CDFs序列中的最大值为MAX。例如：

      IDs为id1、id2、id3..... 
      VALUEs为2、3、4.1...... 
     那么CDFs为2、5、9.1......
   

4. 从0-1中随机抽取一个随机实数，并乘以步骤3中的最大值MAX，假定结果为TARGET。

5. 累计分布函数值序列找到一个位置索引index，使得CDFs[index] >=TARGET > CDFs[index-1]。IDs序列中对应该位置的id就是抽中的个体。

6. 重复步骤4和5，一直到抽取完sampleSize个样本。

与简单随机抽样一样，抽取的样本也需要排重。样本抽取代码如下：

 //ids母体的所有个体的id列表，priorValues对应的先验值，sampleSize需要抽取的样本数量
    public static Long[] sampling(Long[] ids, double[] priorValues, int sampleSize)
    {
        //构建概率累计分布函数序列值
        double[] CDFValues = buildCDFValue(priorValues);
        double maxMeasure = CDFValues[CDFValues.length-1];
        Random random = new Random();
        Set<Long> sampleIds = new HashSet<Long>();

        while(sampleIds.size() < sampleSize)
        {
            double rdVal = random.nextDouble()*maxMeasure;
            //查找该随机值对应的id索引
            int index = findIndex(rdVal, CDFValues);
            sampleIds.add(ids[index]);
        }

        return sampleIds.toArray(new Long[sampleIds.size()]);
    }

累计分布函数值序列构建代码实现如下：

 //计算概率累计分布函数序列值值。
    // CDFValue元素的取值是截止当前id，并包含当前id的所有的先验值的和。
    public static double[] buildCDFValue(double []priorValues)
    {
        double [] CDFValues = new double[priorValues.length];
        double sum = 0;
        for(int i = 0; i < priorValues.length; i++)
        {
            sum += priorValues[i];
            CDFValues[i] = sum;
        }
        return CDFValues;
    }

这次采用二分法查找随机值对应的id索引，代码实现如下：

 static int findIndex(double dst, double[] CDFValues) {
        int min = 0;
        int max = CDFValues.length;

        while (min < max) {
            int middle = (min + max) / 2;

            if (middle < 0) {
                return middle;
            }

            if (Double.compare(dst, CDFValues[middle]) <= 0) {
                if (middle == 0 || Double.compare(dst, CDFValues[middle - 1]) > 0) {
                    return middle;
                }
                max = middle;
            } else {
                if (middle == CDFValues.length - 1) {
                    return middle;
                }
                min = middle;
            }

            if (min > max) {
                System.out.print("");
            }
        }
        return -1;
    }

预测值计算

与简单随机抽样不同，重要性采用的抽样的预测值的计算不是对抽样观测值加和求均值，预测值计算公式应该为$$1/N\sum _{i=1}^{N}xi\ast \frac{p(xi)}{q(xi)}$$
假定母体总数量为T，有效样本数量为N，每个样本对应的观测值序列分别为x1,x2…xN，每个样本id对应的先验值序列为v1,v2…vN，累计分布函数值序列，即CDFs最大值为MAX。预测值流程图如下：

具体计算步骤如下：

1. 将样本先验值序列v1,v2…vN中的每个值除以MAX，也就是计算每个样本id在建议分布的概率值q(x)
2. 将样本观测值序列的每个数除以母体总数量，即x/T。本质上是计算xi*p(xi)。
3. 将步骤2中产生序列中的每个元素除以步骤1中产生序列的对应元素。本质上是计算xi*p(xi)/q(xi)。
4. 将步骤3中计算的元素进行求和，并除以样本数量N。

代码实现如下：

 public static double calculateMean(double [] sampleValues, double[] priorValues, double maxMeasure, int idSize)
    {
        Random random = new Random();
        double sum = 0;
        for(int i = 0; i < sampleValues.length; i++)
        {
            double probability = priorValues[i]/maxMeasure;
            sum += sampleValues[i]/idSize/probability;
        }
        return sum/sampleValues.length;
    }

模拟验证

为了验证重要性抽样的效果，我们将构建一个模拟数据。然后，对该模拟数据分别进行简单随机抽样和重要性抽样，对比这两种抽样方式在方差和偏差方面的表现。

模拟数据构造

我们将构造S、M、L三种类型的数据。每种类型的数据都是由均值和标准差固定的高斯分布函数所生成。具体生成参数如下表：

类型	均值	标准差	数量
S	10	5	8500
M	50	25	1000
L	250	125	500

这个模拟数据构造遵循了两个原则：

它是混合高斯分布。真实世界的很多例子都满足该分布，比如酒店一般分成不同的星级，每个星级内的酒店的价格往往遵循高斯分布，所有酒店的价格就是一个混合高斯分布。

满足长尾效应。均值小的的个体数量远远多于均值大的个体数量。比如，购买10w元小汽车的数量一定远远高于250w以上的汽车的数量。

抽样计划

我们将采用4中抽样方式：简单随机抽样、重要性采样、高估采样、低估采样。

简单随机抽样就是从所有个体中进行随机抽取。在重要性采样方式中，每个个体的先验值等于其对应数据类型的期望值。

在真实世界中，我们当然不可能得到真正的期望值。为了验证建议分布构建的健壮性，我们构建了高估采样和低估采样。所谓的高估和低估都是一个相对值，所以对先验值的高估和低估都体现在M和L类型的个体上。对于高估类型抽样，M类型数据的先验值为真实期望值的1.5倍，M类型数据的先验值为真实期望值的2.25倍（1.51.5）。对于低估类型抽样，M类型数据的先验值为真实期望值67%，M类型数据的先验值为真实期望值的45%（0.670.67）。

对于这四种抽样方式，我们重复抽样200次，用于计算每种抽样方式的偏差和标准差。每次抽样的样本数量为100。

详细抽样计划如下表：

抽样方式	抽样次数	每次抽样样本数量	S类型先验值	M类型先验值	L类型先验值
简单随机抽样	200	100	不适用	不适用	不适用
重要性采样	200	100	10	50	250
高估采样	200	100	10	33.5	112
低估采样	200	100	10	75	562

抽样结果分析

抽样结果统计数据如下表。模拟数据期望值为26.63。抽样均值同一抽样方式下200次抽样的预测值平均值，标准差是这200次抽样预测值之间的标准差。偏差是抽样均值与模拟数据期望值之间的误差。变异系数是用标准差除以抽样均值的结果。

抽样方式	抽样均值	标准差	偏差	变异系数
简单随机抽样	27.00	6.59	0.37	0.24
重要性采样	26.55	1.19	0.08	0.04
高估采样	26.90	1.64	0.27	0.06
低估采样	26.41	1.53	0.22	0.05
模拟数据期望值	26.63	不适用	不适用	不适用

从上表我们看到，不同抽样方式的偏差影响较小，但是简单随机抽样的偏差最大，重要性采用最小。标准差对预测结果的影响很大，简单随机抽样的标准差达到了6.59，是重要性采样的5.53倍。对应的，简单随机抽样变异系数达到24%，是重要性采样的6倍。

健壮性分析

从上表可以看出，无论是高估采样还是低估采样，其结果与重要性采样相比，差别都很小。就标准差基本上维持在一个数量级。这个结果证明了建议分布构建的健壮性，即使先验预估有很大的误差，只要具备合理性，所得到的结果也会远优于简单随机抽样

抽样数据展示

把每种抽样方式的所有200次抽样预测值画成概率直方图如下。可以看出来，简单随机抽样得到的结果分布很广，预测值和实际结果之间可能相差很大。而其他三种抽样方式的预测值非常集中，相互之间图形接近。

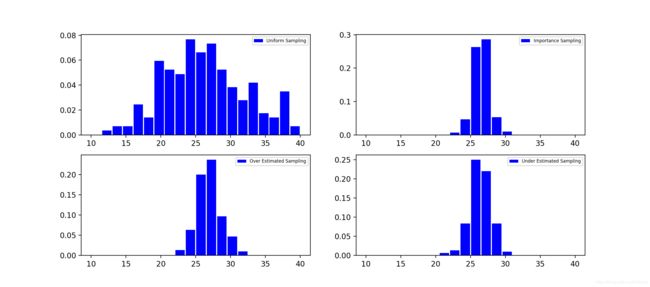
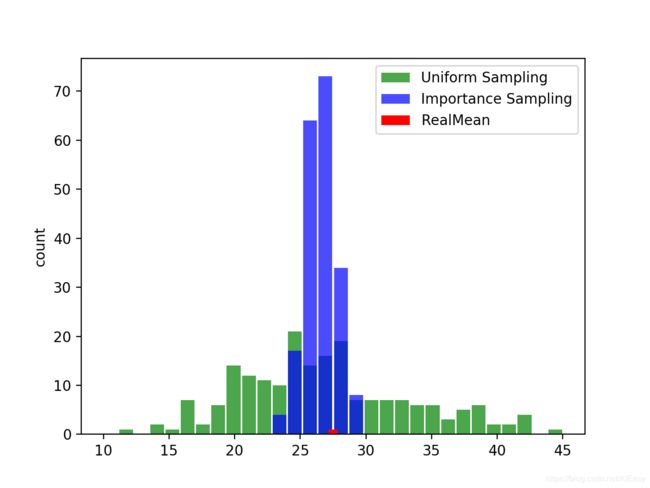
为了更好的对比简单随机抽样和重要性采样的预测效果，我们把这两种抽样结果数据放入同一个直方图中进行对比。如下图，蓝色表示重要性采样，绿色表示简单随机抽样，红色表示期望值。可以看出，重要性采样的结果基本上都3以内，而简单随机抽样的结果误差可以超过19，超过70%的误差。

总结

文章总结了作者进行抽样预测实践时采用的流程，潜在的困难点以及解决方案，采用直观的语言阐述最重要的核心概念。期望能够帮助读者正确地理解预测结果，实施合理的抽样预测实验，减少实验实操过程中的错误。

对于实践中经常碰到样本数量稀缺的问题，文章从理论和模拟数据两方面验证的重要性采样的高效性。对于重要性采样的三个主要步骤：分布概率构建、抽样以及预测值计算，文章都给出了实践建议，计算逻辑和部分代码实现。同时，文章还从定性分析和模拟数据两方面验证了分布概率构建的健壮性。

当然采用重要性采样去做抽样预测，就很难给出置信度、置信区间这样的实验精度数据。对于有兴趣的读者，可以沿着这条路继续深入，尝试去衡量重要性采样的精度。

参考文献

[1]Wikipedia, [Lies, damned lies, and statistics] https://en.wikipedia.org/wiki/Lies,_damned_lies,_and_statistics
[2]Wikipedia, [Importance sampling] https://en.wikipedia.org/wiki/Importance_sampling
[3]S. Sutton R, G. Barto A. Reinforcement Learning: An Introduction (Adaptive Computation and Machine Learning series) second edition Edition
[4]Bengio Y, Sénécal. [Quick Training of Probabilistic Neural Nets by Importance Sampling]
[5]Wikipedia, [Law of large numbers] https://en.wikipedia.org/wiki/Law_of_large_numbers
[6]Wikipedia, [Confidence interval] https://en.wikipedia.org/wiki/Confidence_interval
[7]Wikipedia, [Central limit theorem] https://en.wikipedia.org/wiki/Central_limit_theorem
[8]Wikipedia, [Variance] https://en.wikipedia.org/wiki/Variance
[9]Wikipedia, [Standard score] https://en.wikipedia.org/wiki/Standard_score
[10]Wikipedia, [Binomial_distribution] https://en.wikipedia.org/wiki/Binomial_distribution