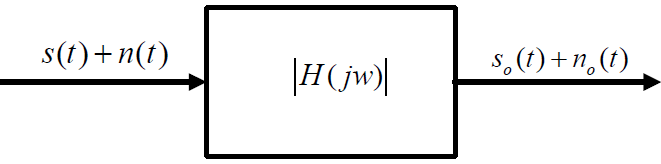线性调频信号 与 脉冲压缩技术的多种实现方法（附MATLAB实现）

线性调频与脉冲压缩

1 线性调频信号

1.1 线性调频信号（时域）

1.1.1 线性调频信号模型

线性调频信号（Chirp, LFM） 是指瞬时频率随时间线性变化的信号。
（1）时域表达式
$$s\left(t\right)=rect\left(\frac{t}{T}\right)\exp \left(j\pi K{t}^2\right)$$
其中，T 为时宽，K 为调频率，rect() 为矩形窗函数。
（2）相位
$$\phi \left(t\right)=\pi K{t}^2$$
（3）瞬时频率
$$f\left(t\right)=\frac{1}{2\pi }\frac{d\phi \left(t\right)}{dt}=\frac{1}{2\pi }\frac{d\left(\pi K{t}^2\right)}{dt}=Kt$$
（4）信号带宽
$$BW=\left|K\right|T$$
（5）时间带宽积
$$TBP=\left|K\right|T^2$$

1.1.2 线性调频信号时域仿真

（1）信号参数
① 时宽 Tr = 1 us
② 带宽 Br = 100 MHz
③ 采样率 Fs = 4 * Br

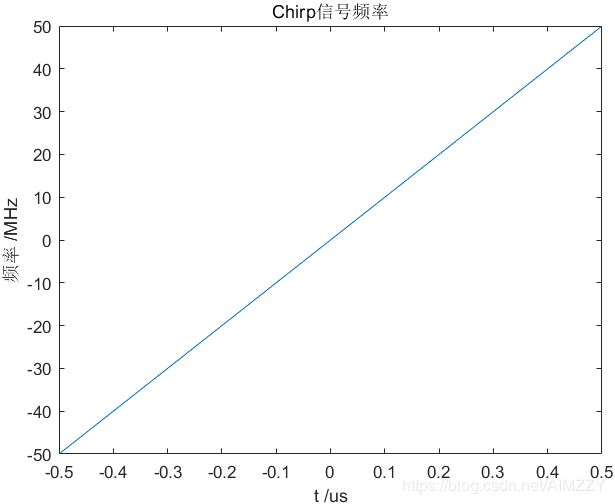
（2）仿真结果

信号实部	信号虚部	信号频率	信号相位

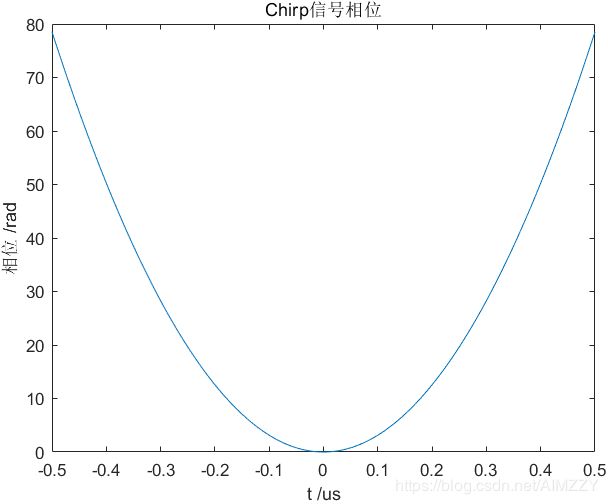1.2 线性调频信号（频域）

1.2.1 驻定相位原理（POSP）

（1）基本原理
  信号在相位驻留点邻域附近是缓变的，而在其他时间点_上是迅变的，相位迅变处由于相位周期的正负部分相互抵消,故其对积分的贡献几乎为零，对积分起主要作用的部分集中在相位驻留点附近。
  因此，驻定相位原理适用于相位包含二次及高次项，且包络缓变的信号频谱求解；’

  对于包络 $w\left(t\right)$ 缓变，且相位 $\varphi \left(t\right)$ 包含高次项的信号
$$g\left(t\right)=w\left(t\right)\cdot \exp \left\{j\cdot \varphi \left(t\right)\right\}$$
根据POSP求解其频谱为：
$$\begin{array}{rl}G\left(f\right)& ={\int }_{-\infty }^{+\infty }w\left(t\right)\cdot \exp \left\{j\cdot \varphi \left(t\right)\right\}\cdot \exp \left(-j2\pi ft\right)dt\\ & ={\int }_{-\infty }^{+\infty }w\left(t\right)\cdot \exp \left\{j\cdot \left[\varphi \left(t\right)-2\pi ft\right]\right\}dt\\ & ={\int }_{-\infty }^{+\infty }w\left(t\right)\cdot \exp \left\{j\cdot \theta \left(t\right)\right\}dt\\ & \stackrel{POSP}{\approx }w\left[t\left(f\right)\right]\cdot \exp \left\{j\cdot \theta \left[t\left(f\right)\right]\right\}\end{array}$$

（2）POSP求解步骤
① 待求解信号
$$g\left(t\right)=w\left(t\right)\cdot \exp \left\{j\cdot \varphi \left(t\right)\right\}$$
其中，包络 $w\left(t\right)$ 缓变，且相位 $\varphi \left(t\right)$ 包含高次项。
② 相位函数
$$\theta \left(t\right)=\varphi \left(t\right)-2\pi ft$$
其中，t 为自变量，f 为参数。
③ 求解驻留点
令：
$$\frac{d}{dt}\theta \left(t\right)=\frac{d}{dt}\left[\varphi \left(t\right)-2\pi ft\right]=0$$
求解方程得到驻留点 $t\left(f\right)$
④ 将驻留点代入频谱得解
$$G\left(f\right)\stackrel{POSP}{\approx }\sqrt{\frac{2\pi }{\left|{\varphi }^{\prime \prime }\left[t\left(f\right)\right]\right|}}\cdot w\left[t\left(f\right)\right]\cdot \exp \left\{j\left[\theta \left(t\left(f\right)\right)+\frac{\pi }{4}\right]\right\}\approx w\left[t\left(f\right)\right]\cdot \exp \left\{j\cdot \theta \left[t\left(f\right)\right]\right\}$$

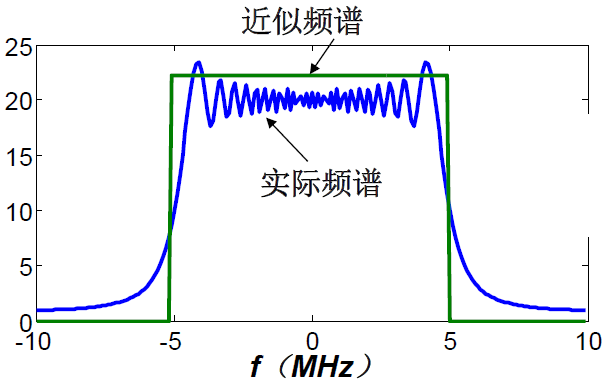
1.2.2 线性调频信号频谱

直接对线性调频信号求傅里叶变换：
$$S\left(f\right)={\int }_{-\infty }^{+\infty }rect\left(\frac{t}{T}\right)\exp \left(j\pi K{t}^2\right)\exp \left(-j2\pi ft\right)dt$$
积分内存在指数上方的二次项积分，无法直接求解。故采用驻点相位定理求解如下：
令相位函数：
$$\theta \left(t\right)=\pi K{t}^2-2\pi ft$$
求导等于0：
$$\frac{d}{dt}\theta \left(t\right)=\frac{d}{dt}\left(\pi K{t}^2-2\pi ft\right)=2\pi Kt-2\pi f=0$$
得驻定相位点为：
$$t\left(f\right)=\frac{f}{K}$$
因此：
$$w\left[t\left(f\right)\right]=rect\left(\frac{t\left(f\right)}{T}\right)=rect\left(\frac{f}{KT}\right)$$
$$\theta \left[t\left(f\right)\right]=\pi K{t}^2\left(f\right)-2\pi ft\left(f\right)=\pi K{\left(\frac{f}{K}\right)}^2-2\pi f\left(\frac{f}{K}\right)=-\pi \frac{f^2}{K}$$
从而得到线性调频信号频谱为：
$$S\left(f\right)=w\left[t\left(f\right)\right]\cdot \exp \left\{j\cdot \theta \left[t\left(f\right)\right]\right\}=rect\left(\frac{f}{KT}\right)\cdot \exp \left\{-j\pi \frac{f^2}{K}\right\}$$

且TBP越大，POSP越准确（因为TBP越大，实际频谱越接近矩形窗）。

1.2.3 线性调频信号频谱仿真

幅度谱	相位谱

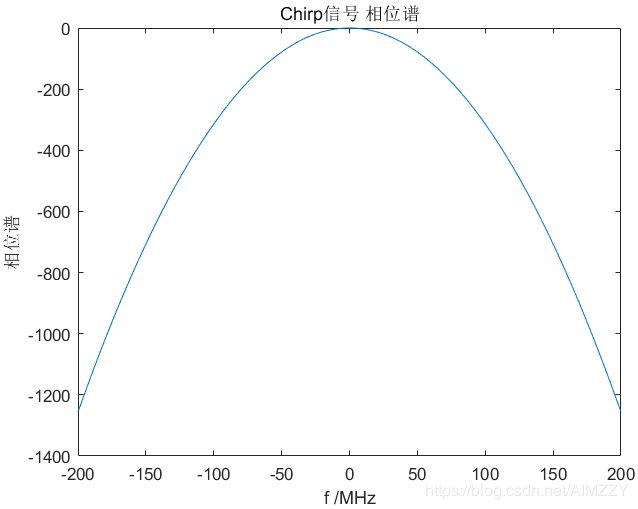2 脉冲压缩

2.1 匹配滤波器

  匹配滤波器是线性系统的最大信噪比滤波器。信号和噪声叠加在一起，匹配滤波使信号成分在某一瞬时出现峰值，而噪声成分受到抑制，即使输出的信噪比最大。

2.1.1 匹配滤波器推导

设 t=tm 时刻输出信噪比最大，信噪比表示为：
$$\rho =\frac{s_o^2\left(t_m\right)}{n_o^2\left(t_m\right)}$$
利用频域表达式可得输出信号为：
$$s_o\left(t\right)={\mathcal{F}}^{-1}\left\{S\left(j\omega \right)H\left(j\omega \right)\right\}=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }S\left(j\omega \right)H\left(j\omega \right)\exp \left(j\omega t\right)d\omega$$
白噪声平均功率为：
$$\overline{n_o^2\left(t\right)}=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }N\cdot {\left|H\left(j\omega \right)\right|}^{2}d\omega$$
则信噪比可表示为：
$$\rho =\frac{s_o^2\left(t_m\right)}{\overline{n_o^2\left(t_m\right)}}=\frac{{\left|{\int }_{-\infty }^{+\infty }S\left(j\omega \right)H\left(j\omega \right)\exp \left(j\omega t_m\right)d\omega \right|}^2}{2\pi N\cdot {\int }_{-\infty }^{+\infty }{\left|H\left(j\omega \right)\right|}^{2}d\omega }$$
根据柯西不等式：
$${\left|{\int }_{-\infty }^{+\infty }H\left(j\omega \right)S\left(j\omega \right)\exp \left(j\omega t_m\right)d\omega \right|}^2⩽{\int }_{-\infty }^{+\infty }{\left|H\left(j\omega \right)\right|}^{2}d\omega \cdot {\int }_{-\infty }^{+\infty }{\left|S\left(j\omega \right)\exp \left(j\omega t_m\right)\right|}^{2}d\omega$$
当且仅当
$$H\left(j\omega \right)=k{\left[S\left(j\omega \right)\exp \left(j\omega t_m\right)\right]}^{\ast }$$
时，等号成立，即信噪比取得最大值。

最终，得到匹配滤波器为
$$H\left(j\omega \right)=k\cdot S\left(-j\omega \right)\cdot \exp \left(-j\omega t_m\right)$$
两端同取傅里叶逆变换，并根据傅里叶变换的频移性质可得：
$$h\left(t\right)=k\cdot \overline{s\left(t_m-t\right)}$$
一般地，取$k=1,t_m=0$
$$h\left(t\right)=\overline{s\left(-t\right)}$$

2.1.2 匹配滤波器理解

匹配滤波器系统输出为：
$$s_o\left(t\right)=s\left(t\right)\ast h\left(t\right)={\int }_{-\infty }^{+\infty }s\left(\tau \right)h\left(t-\tau \right)d\tau$$
由于 $h\left(t\right)=\overline{s\left(-t\right)}$，因此输出也可写作
$$s_o\left(t\right)={\int }_{-\infty }^{+\infty }s\left(\tau \right)\overline{s\left(\tau -t\right)}d\tau$$

可见，匹配滤波的过程可看作接收信号sr与系统冲激响应ht的卷积

so = conv( sr , ht) = conv( sr , conj(fliplr( si )) );

也可看作发射信号si与接收信号sr的相关。

so = xcorr( sr , si );

2.2 线性调频信号脉冲压缩的匹配滤波实现

对于线性调频信号，时域为：
$$s\left(t\right)=rect\left(\frac{t}{T}\right)\exp \left(j\pi K{t}^2\right)$$
频谱为：
$$S\left(f\right)=rect\left(\frac{f}{KT}\right)\cdot \exp \left\{-j\pi \frac{f^2}{K}\right\}$$

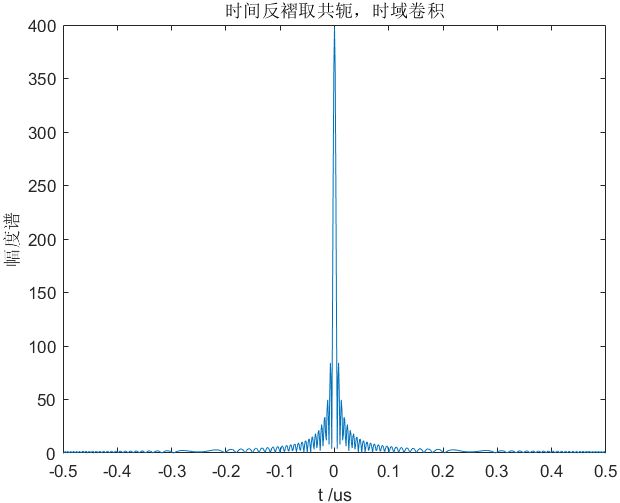
2.2.1 时域匹配滤波

根据 $h\left(t\right)=\overline{s\left(-t\right)}$ 可构造时域匹配滤波器为发射信号时间反褶再取共轭。再与发射信号进行线性卷积即可实现脉冲压缩：
$$s_o\left(t\right)=s\left(t\right)\ast \overline{s\left(-t\right)}$$

2.2.2 频域匹配滤波

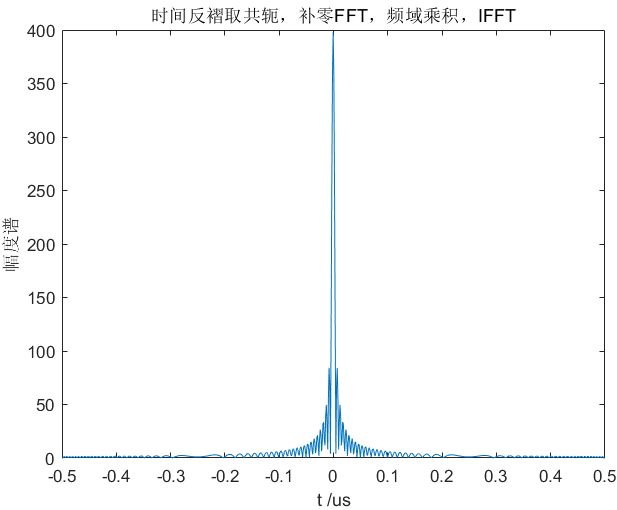
2.2.2.1 方法一

（1）原理

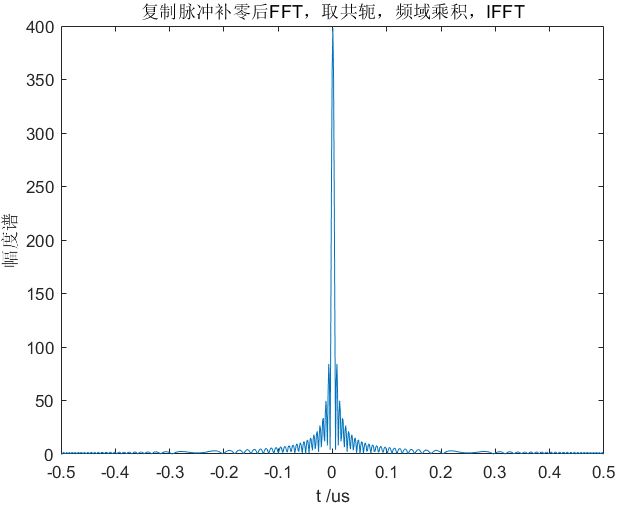
将发射信号时间反褶后取共轭，补零后计算FFT；再与信号补零后的FFT在频域相乘，最后IFFT。
$$s_o\left(t\right)=\mathcal{I}\mathcal{F}\mathcal{F}\mathcal{T}\left\{\mathcal{F}\mathcal{F}\mathcal{T}\left[\overline{s\left(-t\right)},N\right]\cdot \mathcal{F}\mathcal{F}\mathcal{T}\left[s\left(t\right),N\right]\right\}$$

（2）说明

• 为什么需要补零？
  因为匹配滤波需要计算线性卷积，但 (DFT) FFT 计算的是循环卷积，所以需要对信号进行补零直到长度超过线性卷积的长度。对于点数分别为N1与N2的两信号，它们线性卷积的长度为 N1+N2-1；若循环卷积长度为N，则有如下关系：
  ① N < N1 + N2 - 1 时，循环卷积是线性卷积长度为 N 的混叠
  ② N = N1 + N2 - 1 时，循环卷积 = 线性卷积
  ③ N > N1 + N2 - 1 时，循环卷积 = 线性卷积末尾补 N-(N1+N2-1) 个 0 （弃置区）

• 弃置区位置
  由于发射是反褶后再补零，故最终得到IFFT结果后，弃置区位于信号前端。

（3）仿真

2.2.2.2 方法二

（1）原理

将发射脉冲补零后进行FFT，再取共轭（无需反褶），与信号补零FFT在频域相乘，最后IFFT。
$$s_o\left(t\right)=\mathcal{I}\mathcal{F}\mathcal{F}\mathcal{T}\left\{\overline{\mathcal{F}\mathcal{F}\mathcal{T}\left[s\left(t\right),N\right]}\cdot \mathcal{F}\mathcal{F}\mathcal{T}\left[s\left(t\right),N\right]\right\}$$

（2）说明

• 方法二与方法一的关系：
  根据傅里叶变换的性质，时域共轭+反褶 ↔ 频域共轭（方法一）；因此，也可先变换到频域再取共轭（方法二）。但由于它们补零时存在是否反褶的差别，故最终结果的弃置区也存在反褶。

• 弃置区位置
  由于发射是直接在末尾补零，故最终得到IFFT结果后，弃置区位于信号末端。

（3）仿真

2.2.2.3 方法三

（1）原理

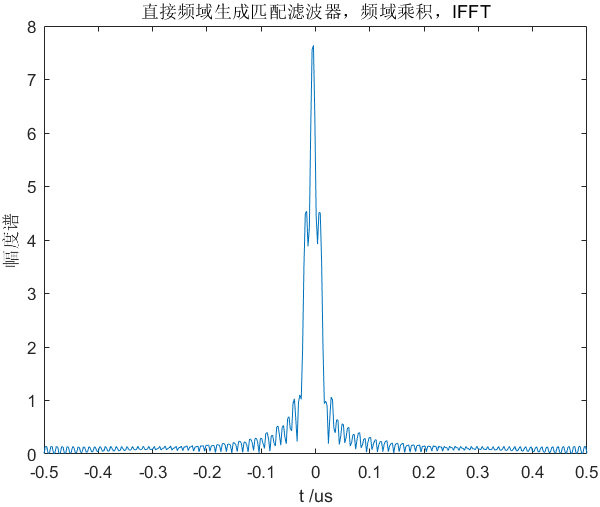
直接在频域生成匹配滤波器
$$H\left(f\right)=rect\left\{\frac{f}{\left|K\right|T}\right\}\exp \left\{j\pi \frac{f^2}{K}\right\}$$
与信号FFT在频域相乘，最后IFFT。
$$s_o\left(t\right)=\mathcal{I}\mathcal{F}\mathcal{F}\mathcal{T}\left\{\mathcal{F}\mathcal{F}\mathcal{T}\left[s\left(t\right)\right]\cdot H\left(f\right)\right\}$$

（2）仿真

2.3 加窗处理

2.3.1 性能指标

（1）冲激响应宽度（IRW），冲激响应的 3dB 宽度。
（2）峰值旁瓣比（PSLR），最大旁瓣与峰值的高度比。
（3）积分旁瓣比（ISLR），旁瓣能量与主瓣能量的比值。

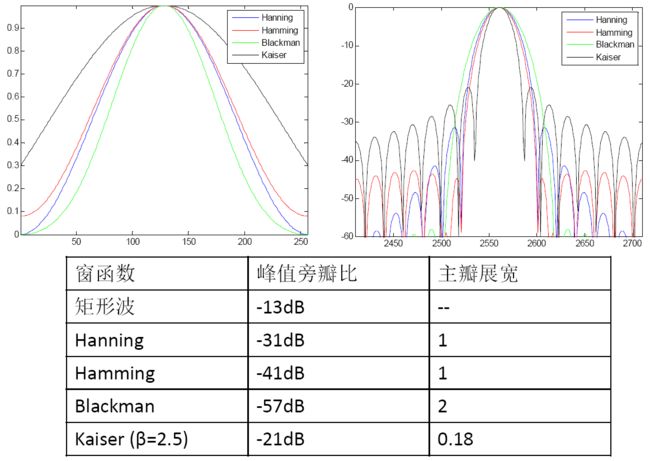
2.3.2 各类窗效果对比

2.3.3 脉冲压缩加窗

窗名	频谱加窗	脉压结果
矩形窗
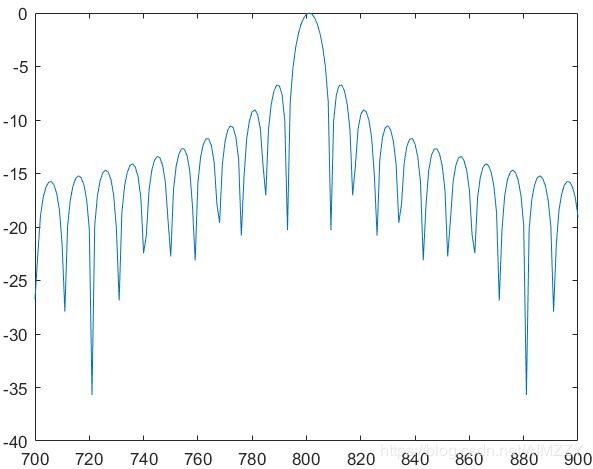三角窗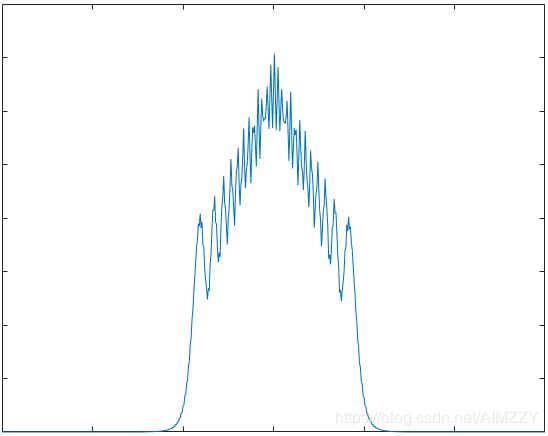
汉宁窗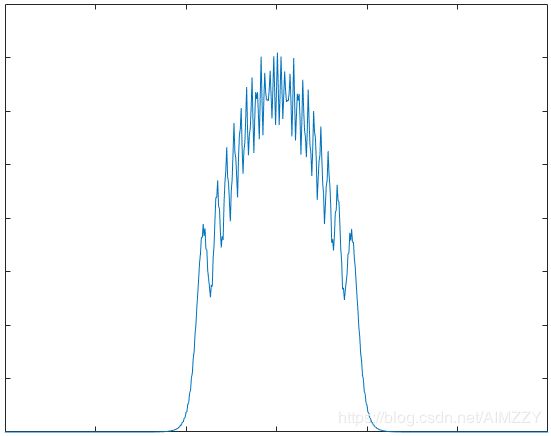
汉明窗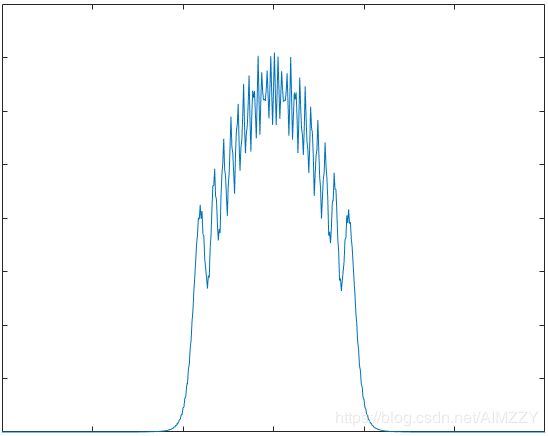
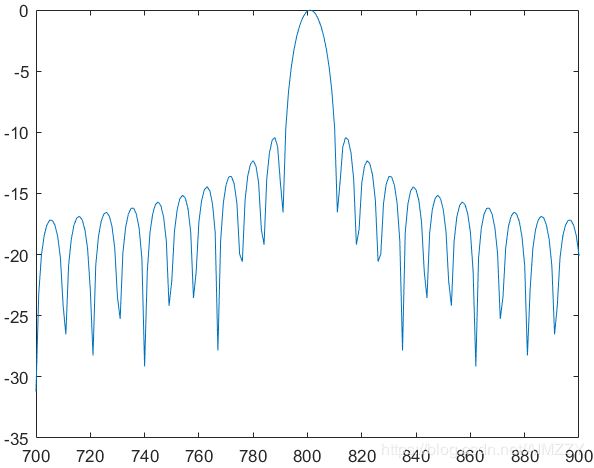布莱克曼窗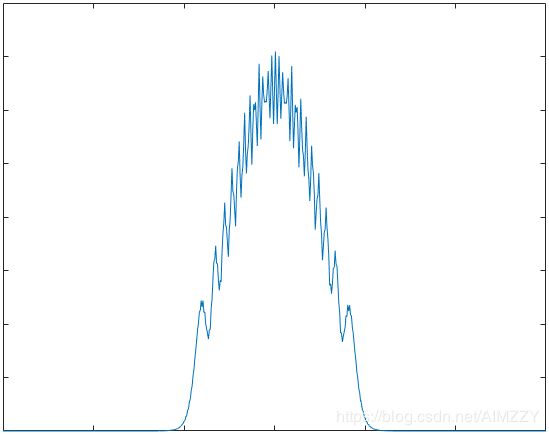

3 脉冲压缩测距仿真

3.1 实现流程

• 参数设置
  信号时宽 T = 6 us 信号带宽 B = 400 MHz 目标距离 R = [ 995, 1000, 1001, 1005 ] m 后向散射 σ = [ 1, 1.5 , 2.25, 3.375]
• 系统参数导出
  采样率 Fs = 5 * B 调频率 K = B / T 采样点数 N = round( T * Fs )
• 目标参数导出
  目标个数 M = length( R ) 中心距离 R0 = mean( R ) 最大探测距离范围 Rwid = T * c / 2 最远探测距离 Rmax = floor( R0 + Rwid / 2 ) 最近探测距离 Rmax = floor( R0 - Rwid / 2 )
• 回波参数
  发射时间序列 t = linspace( 2 * Rmin / c , 2 * Rmax / c , N ) 回波时间序列 td = t - 2 * R / c
• 回波信号
  $$s_r\left(t\right)=\sigma \cdot rect\left(\frac{t_d}{T}\right)\cdot \exp \left(j\pi K\cdot t_d^2\right)$$
• 脉冲压缩
  方式2
  $$s_o\left(t\right)=\mathcal{I}\mathcal{F}\mathcal{F}\mathcal{T}\left\{\overline{\mathcal{F}\mathcal{F}\mathcal{T}\left[s_t\left(t\right),N_{fft}\right]}\cdot \mathcal{F}\mathcal{F}\mathcal{T}\left[s_r\left(t\right),N_{fft}\right]\right\}$$
• 弃置区处理
  脉压信号起始点 N0 = ( Nfft - N ) / 2 脉压信号截取 so = so( N0 , N0 + N -1 )
• 绘图

3.2 仿真结果

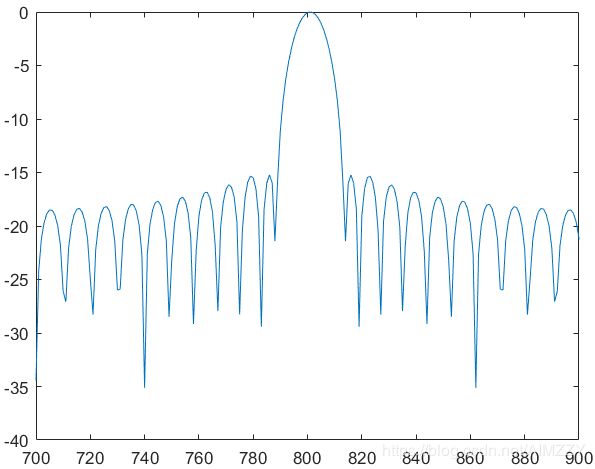
回波信号	脉压测距结果	脉压测距结果（局部放大）/dB

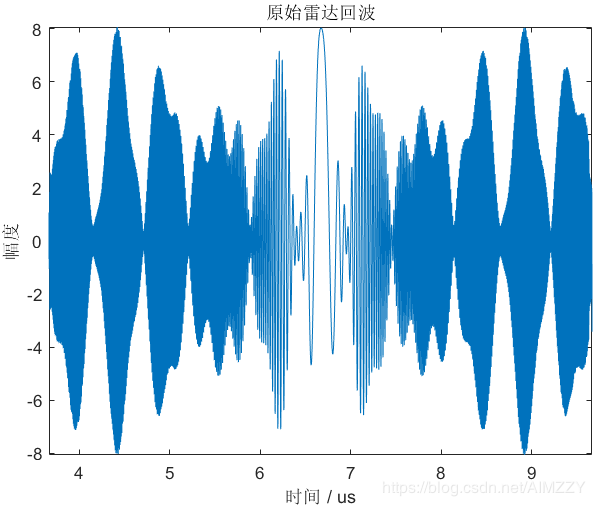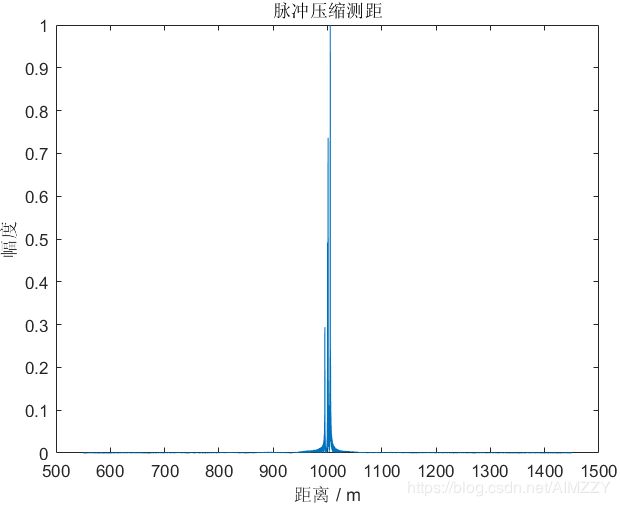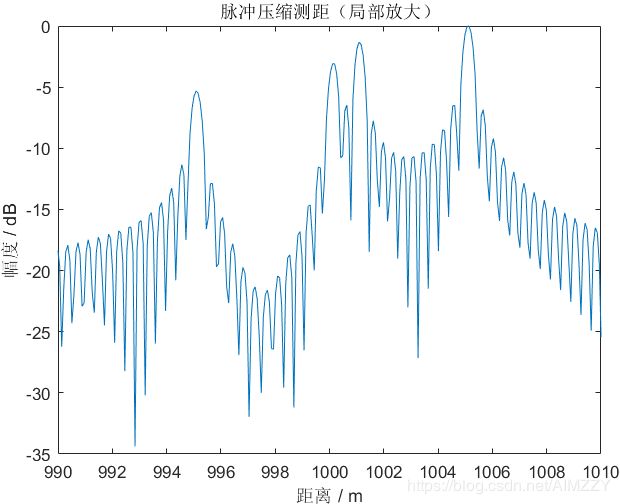附录：MATLAB程序

全部完整程序

• 线性调频与脉冲压缩MATLAB
• 脉冲压缩测距MATLAB

部分测试程序

• 线性调频与脉冲压缩

%% 线性调频与脉冲压缩
clear,clc,close all
set(0,'defaultfigurecolor','w')
%% Chirp信号参数设置
Tr = 1e-6;%时宽
Br = 200e6;%带宽
Fs = 4*Br;%采样率
%% Chirp信号参数导出
Kr = Br/Tr;%调频率
N =  round( Tr / (1/Fs) );%采样点数
t = linspace( -Tr/2 , Tr/2 , N);%在[-Tp/2,Tp/2]选取采样点
%% Chirp信号生成
st = ( abs(t) < Tr/2 ) .* exp( 1j * pi * Kr * t.^2 ); 
f_chirp= Kr * t; %信号频率
phase_chirp = pi * Kr * t.^2;%信号相位
%% 频谱
freq = linspace(-Fs/2,Fs/2,N);%频域采样
Sf = fftshift( fft(st) );
%% 时域匹配滤波
ht = conj( fliplr(st) ); %时域匹配滤波为发射信号时间反褶再取共轭
s1 = conv(st,ht); %线性调频信号经过匹配滤波器后的输出(时域卷积)
N1 = N+N-1 ;%线性卷积后信号长度变为 N1+N2-1
t1 = linspace( -Tr/2 , Tr/2 , N1);
%% 频域匹配滤波1 (复制发射脉冲进行时间反褶并取共轭，计算补零DFT)
N2 = 2*N; %循环卷积长度 （N2应当>=N+N-1，其中弃置区位于长度大于N+N-1的部分）
t2 = linspace( -Tr/2 , Tr/2 , N2);
Hf2 = fft(ht,N2); %频域匹配滤波器
Sf2 = fft(st,N2);%频域信号
S2 = Sf2 .* Hf2;%频域乘积
s2 = ifft(S2);
%% 绘图
% 时域
figure,plot( t*1e6, real(st) ),xlabel('t /us'),ylabel('幅度'),title('Chirp信号实部');
figure,plot( t*1e6, imag(st) ),xlabel('t /us'),ylabel('幅度'),title('Chirp信号虚部');
figure,plot( t*1e6, f_chirp/1e6 ),xlabel('t /us'),ylabel('频率 /MHz'),title('Chirp信号频率');
figure,plot( t*1e6, phase_chirp ),xlabel('t /us'),ylabel('相位 /rad'),title('Chirp信号相位');
% 频域
figure,plot( freq/1e6,abs(Sf) ),xlabel('f /MHz'),ylabel('幅度谱'),title('Chirp信号 幅度谱');
figure,plot( freq/1e6,-pi*freq.^2/Kr ),xlabel('f /MHz'),ylabel('相位谱'),title('Chirp信号 相位谱');
% 时域匹配滤波
figure,plot( t1*1e6 , abs(s1) ),xlabel('t /us'),ylabel('幅度谱'),title('时间反褶取共轭，时域卷积');
% 频域匹配滤波1

• 脉冲压缩测距

%线性调频脉冲压缩测距
clear,clc,close all
%% 参数设置
T = 6e-6;%信号持续时间(脉冲宽度6us)
B = 400e6;%信号调频带宽(40MHz)
Fs = 5*B;%采样率
R = [995,1000,1001,1005];%目标距离
RCS = [1 1.5 2.25 3.375];%目标有效面积
%% 导出参数
%系统参数
C = 3e8; 
K = B/T;%调频率
Ts = 1/Fs; %时域采样间隔
N = round(T/Ts);%时域采样点数
%目标参数
M = length(R);%目标的个数
R0 = mean(R);%参考中心距离(用于保证目标在一个回波探测距离内)
Rwid = T * C/2;%能观察到的最大距离范围(最远距离-最近距离) 
Rmax = floor( R0 + Rwid/2 );%观测目标距雷达的最远位置  
Rmin = floor( R0 - Rwid/2 );%观测目标距雷达的最近位置
%回波参数
t = linspace(2*Rmin/C,2*Rmax/C,N);
td = ones(M,1)*t - 2 * R'/C * ones(1,N);
%% 回波信号
Srt = RCS * ( exp(1j*pi*K*td.^2) .* (abs(td)