MATLAB数字信号处理（2）LFM脉冲雷达回波处理仿真

将上学期的“气象雷达原理与系统”课程报告放到blog上。

---

摘要

线性调频（LFM）信号是应用广泛的一种波形，主要优点是脉冲压缩的形状和信噪比对多普勒频移不敏感，即在目标速度未知的情况下，用匹配滤波器仍可以实现回波信号的脉冲压缩，这将大大有利于雷达对目标的探测和信号处理效率的提高。本设计实现了对线性调频（LFM）脉冲压缩雷达的工作原理仿真，在MATLAB 平台中模拟一个叠加的线性调频回波信号，对该信号分别进行采样解调、滤波抽取、脉冲压缩，提取出其中包含的测量物体的距离信息，实验效果良好。

---

Abstract

The linear frequency modulation (LFM) signal is a widely used waveform. The main advantage is that the shape and signal-to-noise ratio of pulse compression are not sensitive to Doppler shift. That is, if the target speed is unknown, the matched filter is still used. Pulse compression of the echo signal can be achieved, which will greatly benefit the radar’s detection of the target and the improvement of signal processing efficiency. This design realizes the simulation of the working principle of linear frequency modulation (LFM) pulse compression radar. In the MATLAB platform, a superimposed chirp echo signal is simulated, and the signal is sampled, demodulated, filtered and compressed, and the distance information of the measured object is extracted. The experimental results are good.

---

1、引言

1.1 作用距离和距离分辨力

作用距离和距离分辨力是雷达最重要的两个技术指标。作用距离取决于发射信号的能量，发射信号的能量又与发射脉冲的功率和发射时间（即脉冲宽度）成正比。前者受发射管峰值功率和传输线功率损耗等的限制，成本高且调节范围有限。因此，在发射机峰值功率受限的情况下，只能通过增加脉冲宽度的方法来增加信号能量以增大雷达的作用距离。

雷达的距离分辨力取决于发射信号带宽，带宽越大，距离分辨力越好。传统脉冲雷达发射的是单频信号，脉冲宽度越窄，信号带宽就越宽，距离分辨率就越好。然而发射窄脉冲必然导致平均功率下降，进而减小雷达的作用距离。因此，传统的脉冲雷达中，增大作用距离和提高雷达的分辨力之间存在矛盾。

为了兼顾雷达的作用距离和距离分辨力，发射信号应同时具备大时宽和大带宽的特点，为此，研究人员利用复杂波形来替代传统的单频脉冲信号。在发射端调制信号的频率或相位以增大信号的带宽，并发射大时宽的信号以保证作用距离。在接收端通过匹配滤波器，将接收到的宽脉冲信号进行脉冲压缩得到窄脉冲信号，提高距离分辨率，从而兼顾了作用距离和距离分辨力。这是雷达隐蔽、抗干扰、区分多目标的重要手段。研究最早且应用最广泛的复杂波形便是线性调频信号。

1.2 线性调频信号

雷达波形设计中，采用线性调频信号的优势在于信号产生方便，同时当目标回波存在多普勒频移时脉压结果变化较小，缺点是经过脉压处理后副瓣较高，固定为13.6dB，虽然可以通过加窗的方法对其进行抑制，但同时对信号的其他特性也会带来损失，另外在时宽带宽积小于20时，主瓣副瓣比会变小，导致性能恶化。

线性调频信号的产生方法在早期雷达中使用的是通过全通移相网络、压控振荡器或色散延迟线的方法，后来采用声表面波器件通过模拟手段形成。而新一代雷达一般则使用DDS技术直接合成。脉冲压缩处理方法在现代雷达中一般采用数字方式进行。有两类方式，一类是在频域上进行处理，将零中频回波信号进行快速傅里叶变换然后与发射信号的频谱相乘，然后再进行逆傅里叶变换得出结果；另一类是时域处理法，将零中频信号与回波信号进行卷积直接得出结果。

早期，由于FPGA硬件水平较低，无法进行大量的乘法并行运算，所以主要使用DSP以第一类方法为主。目前随着FPGA的设计制造工艺水平逐步提高，使用FPGA来实现各种雷达信号处理算法乃至整个雷达信号处理系统成为了一种数字信号处理的发展趋势。
本文设计实现了对线性调频（LFM）脉冲压缩雷达的工作原理仿真，在MATLAB 平台中模拟一个叠加的线性调频回波信号，对该信号分别进行采样解调、滤波抽取、脉冲压缩，提取出其中包含的测量物体的距离信息。

---

2、原理分析

2.1 LFM 脉冲雷达原理分析

雷达是利用无线电波来检测目标并测定目标的有无、目标斜距、目标角位置、目标相对速度等的装置。雷达发射机的任务是产生符合要求的雷达波形，然后经馈线和收发开关由发射天线辐射出去，遇到目标后，电磁波一部分反射，经接收天线和收发开关由接收机接收，对雷达回波信号做适当的处理就可以获知目标的相关信息。

假设目标与雷达的相对距离为 R，雷达发射信号s(t) ,传播速度为光速C ，则经过时间R/C后电磁波到达目标，照射到目标上的电磁波可写成：s(t-R/C)。电磁波与目标相互作用，一部分电磁波被目标散射，被反射的电磁波为σ·s(t-R/C)，其中σ为目标的雷达散射截面（RCS）。再经过时间R/C后，被雷达接收天线接收的信号为σ·s(t-2 R/C)。

图 2.1 雷达等效于 LTI 系统

如果将雷达天线和目标看作一个系统，便得到如图 2.1 的等效，而且这是一个 LTI（线性时不变）系统。

等效 LTI 系统的冲激响应可写成：

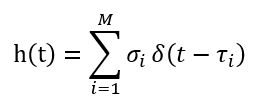
M 表示目标的个数，σ_i是目标散射特性，τ_i是光速在雷达与目标之间往返一次的时间：

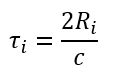
式中， Ri 为第 i 个目标与雷达的相对距离。雷达发射信号 s(t) 经过该 LTI 系统，得输出信号（即雷达的回波信号）sr (t) ：

从雷达回波信号sr (t)提取出表征目标特性的τ_i（表征相对距离）的常用方法如图2.2所示。

图 2.2 雷达回波信号处理

以上便是线性调频（LFM）脉冲压缩雷达的工作原理。

2.2数字下变频原理分析

本设计中可以选用降低采样率来实现数字下变频的目的，原理如图2.3所示。

图 2.3 降低采样率实现数字下变频

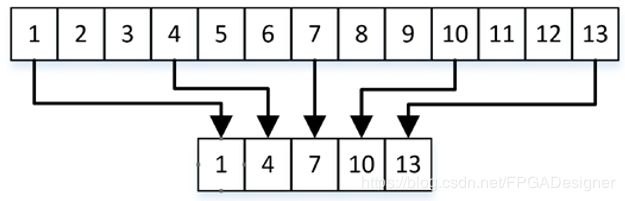
如果原信号采样率为f，则经过n点重采样处理后，采样频率变为f/n。

2.3脉冲压缩原理分析

脉冲压缩相当于让 sr(t) 通过雷达发射信号s(t)的匹配滤波器。s(t)的匹配滤波器hr (t)为：

于是进行滤波处理有：

对上式进行傅立叶变换：

如果选取合适的s(t)，使它的幅频特性|S(jω)|为常数，那么2.6式可写为：

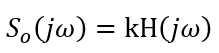
其傅立叶反变换为：

so (t)中包含目标的特征信息τi和σi。从so(t)中可以得到目标的个数M和每个目标相对雷达的距离：

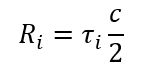
实现脉冲压缩的方式有两种，一种是直接在时域卷积（滤波）法，另一种是在频域中进行处理，如图 2.4 所示。

图 2.4 频域脉冲压缩处理

---

3、详细设计

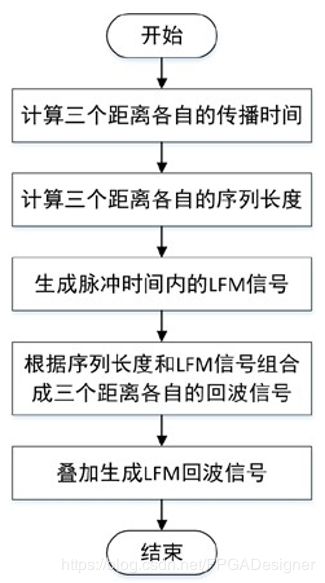
3.1 线性调频信号回波产生模块

表3.1 关键系统参数

参数	含义
f	调频信号基础频率 10MHz
fs	采样频率 100MHz
ts	采样周期 1/fs
B	调频范围 10MHz
T	脉冲宽度 10μs
c	信号传播速度 3×108m/s
PRT	脉冲周期 500μs

本系统中使用到的关键系统参数如表3.1所示。基于上述参数，本系统中使用的线性调频信号为：

本系统假设该线性调频信号检测到三个目标，距离分别为 10km，30km和31km。本模块使用到的主要信号如表3.2所示。

表 3.2 回波信号生成模块信号

信号	含义
y	基础线性调频信号
y1	10km 处的回波信号
y2	30km 处的回波信号
y3	31km 处的回波信号
xt	叠加后的回波信号

线性调频信号回波产生模块的程序设计流程图如图3.1所示。

图3.1 LFM信号回波产生模块程序流程图

程序设计时先计算出三个距离所对应的传播时间，然后根据时间计算出其对应的序列长度，建立三个子信号分别作为三个距离上的回波信号。之后再设计一个 10μs 的 LFM 信号。每一个回波信号由传播时间、10μs的LFM信号、补零三部分组成，总时长为 PRT。最后将三个回波信号叠加起来。

3.2 回波信号采样解调模块

该模块使用一个基础频率的信号进行解调：

本模块使用到的主要信号如表3.3所示。

表3.3 回波信号采样解调模块信号

信号	含义
xt	LFM 叠加的回波信号
yf	相干载波信号
xrt	解调后的信号

相干解调的过程只需要让 xt 和 yf 相乘即可，相乘结果即为解调出来的雷达信号。

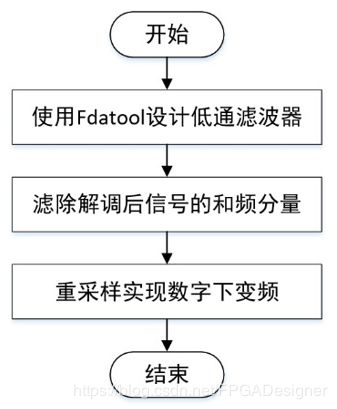
3.3 滤波抽取模块

解调后的信号xrt中包含有两信号相乘的和频信号和差频信号，本模块滤除掉和频信号分量，之后对滤波后的信号重采样，以降低采样率达到数字下变频的目的。本模块使用到的主要信号如表 3.4 所示。

表3.4 滤波抽取模块信号

信号	含义
xrt	解调后的信号
firxrt	滤波后的信号
xrtdown	数字下变频处理后的信号

滤波抽取模块的程序设计流程图如图3.2所示。

图 3.2 滤波抽取模块程序流程图

由于回波信号为10-20MHz，与10MHz的相干信号相乘，结果频谱应该包含 0-10MHz和20-30MHz两个频段，因此使用fdatool设计一个低通滤波器滤除掉20~30MHz的信号。滤波器通带频率15MHz，阻带频率18MHz，通带衰减1dB，阻带衰减1dB，将系数导出到工作空间供滤波处理调用。

对滤波后的信号使用downsample函数进行4位的抽取，则抽取后的信号采样频率变为100Mhz/4=25MHz。

3.4 脉冲压缩模块

表3.5 脉冲压缩模块信号

信号	含义
xrtdown	数字下变频处理后的信号
hdt	匹配滤波信号
out	脉冲压缩处理后的信号

脉冲压缩模块让下变频后的回波信号通过发射信号的匹配滤波器，提取出每个目标回波的距离信息。脉冲压缩有时域法和频域法两种。本模块使用到的主要信号如表3.5所示。匹配滤波信号hdt如公式3.3所示。

匹配滤波信号中的f0为0Hz。时域法进行脉冲压缩使用hdt与xrtdown直接进行卷积即可。频域法进行脉冲压缩按照图2.4中的原理框图处理。

---

4、仿真分析

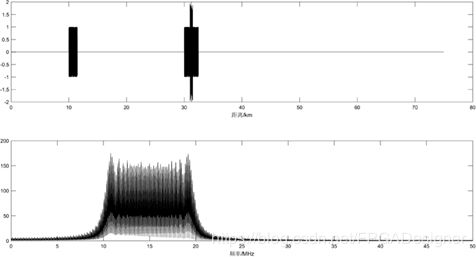
4.1 回波产生模块仿真分析

绘制出雷达回波信号的时域图与频域图，结果如图4.1所示。

图 4.1 雷达回波信号时域与频域

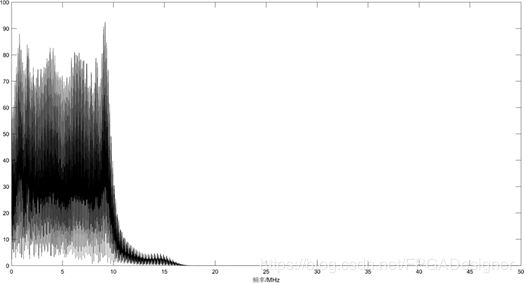
时域中可以看到在10km、30km、31km处看到三个脉冲波形，其中在30km和 31km的交界处发生了信号叠加。频域中信号的频率范围在10MHz至20MHz间线性分布，符合预期设定。

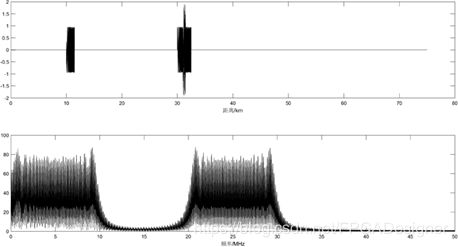
4.2 采样解调模块仿真分析

图 4.2 解调后信号时域图和频域图

绘制出解调，即相乘后的信号时域和频域图，如图4.2所示。时域中可以仍然保留了10km、30km、31km处的三个脉冲波形信息。由于回波信号为10~20MHz，与10MHz的相干信号相乘，结果频谱应该包含0-10MHz和20-30MHz两个频段，因此该模块设计符合预期设定。

4.3 滤波抽取模块仿真分析

绘制对解调信号滤波后的信号频域如图4.3所示。

图 4.3 解调信号滤波后频域图

经过低通滤波后，解调信号中的 20~30MHz 频段被滤除，只留下 0~10MHz频段信号。对该信号抽取后绘制频域如图4.4所示。

图4.4 抽取后信号频域图

抽取后信号仍保留了0~10MHz的信号信息，但采样频率由100MHz降至25MHz，图4.3中最大频率为100MHz/2=50MHz，图4.4中最大频率为25MHz/2=12.5MHz，表明该模块设计符合预期设定。

4.4 脉冲压缩模块仿真分析

脉冲压缩处理后绘制信号的时域图如图4.5所示。

图 4.5 脉冲压缩后信号时域图

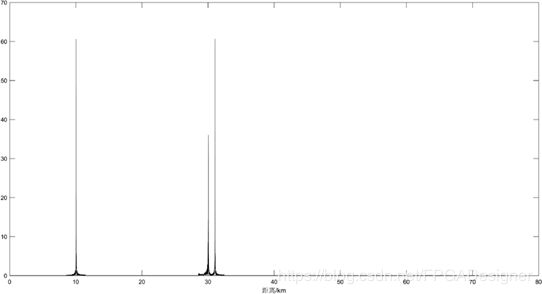
原来每个距离的回波信号脉宽为10μs，经过脉冲压缩后，每个脉冲变为10μs/100=0.1μs。从图4.5中可以清楚的看到在10km、30km、31km处各有一个很窄的脉冲。脉冲压缩处理的能力也决定了雷达信号处理系统的距离分辨力大小， 压缩后脉冲越窄，距离分辨力越大。

---

5、结束语

本设计实现了对线性调频（ LFM）脉冲压缩雷达的工作原理仿真，在MATLAB 平台中模拟一个叠加的线性调频回波信号，对该信号分别进行采样解调、滤波抽取、脉冲压缩，提取出其中包含的测量物体的距离信息，实验效果良好。

脉冲压缩的原理就是使用一个发射信号与接收回波进行相关，可以将较宽的回波信号“压缩”成很窄的信号。压缩后的脉冲宽度决定了可以分辨的最小距离。例如两个目标的回波信号重叠在一起，在回波信号中无法直接分辨出两个目标的位置，未进行脉冲压缩的雷达距离分辨力 ΔR=(cτ)/2=c/(2B)。这种体制的雷达要提高距离分辨率必须减小脉冲宽度，脉宽减少会降低平均发射功率，使用线性调频信号进行脉冲压缩可以实现提高距离分辨率而保持平均发射功率。脉冲压缩后的距离分辨力 ΔR=(cτ’)/2<<(cτ)/2。

---

MATLAB代码如下（fir.mat放不上来，按照文中参数使用FDATOOL工具设计导出即可）：

% written by 刘奇

clc;
clear;
close all;

f = 10000000;         %10MHz
fs = 100e6;
ts = 1 / fs;
B = 10^7;
T = 10^(-5);
u = B / T;
c = 3e8;
PRT = 500e-6;


r1 = 10000;   tao1 = 2*r1/c;  n1 = round(tao1 / ts);
r2 = 30000;  tao2 = 2*r2/c;  n2 = round(tao2 / ts);
r3 = 31000;  tao3 = 2*r3/c;  n3 = round(tao3 / ts);
NN = PRT / ts;

t1 = 0 : ts : T-ts;
y = sin(2*pi*(f*t1+0.5*u*t1.^2));
N = length(y);


y1 = [zeros(1, n1), y, zeros(1, NN-n1-N)];
y2 = [zeros(1, n2), y, zeros(1, NN-n2-N)];
y3 = [zeros(1, n3), y, zeros(1, NN-n3-N)];
xt = y1+y2+y3;
figure;
subplot(2, 1, 1);
plot((0:length(xt)-1)*ts*c/2/1000, xt);
xlabel('距离/km');
xtfft = abs(fft(xt, 50000));
subplot(2, 1, 2);
fx=(0:length(xt)/2-1)*fs/length(xt);
plot(fx/1e6, xtfft(1:length(xt)/2));
xlabel('频率/MHz');

% 对回波信号采样
fs1 = 100e6;
ts1 = 1/fs1;
t2 = 0 : ts1 : (length(xt)-1)*ts1;
xrt = xt .* sin(2*pi*f*t2);

fx1=(0:length(xt)/2-1)*fs1/length(xt);
figure;
subplot(2, 1, 1);
plot((0:length(xt)-1)*ts*c/2/1000, xrt);
xlabel('距离/km');
xrtfft = abs(fft(xrt, 50000));
subplot(2, 1, 2);
fx1=(0:length(xrt)/2-1)*fs1/length(xrt);
plot(fx1/1e6, xrtfft(1:length(xrt)/2));
xlabel('频率/MHz');

load fir.mat
firxrt = filter(Num, 1,  xrt);
firfft = abs(fft(firxrt, 50000));
figure;
plot(fx1/1e6, firfft(1:length(firxrt)/2));
xlabel('频率/MHz');
xrtdown = downsample(firxrt, 4);
 value0=abs(fft(xrtdown));%FFT分析
figure;
fx1=(0:length(xrtdown)/2-1)*(fs1/4)/length(xrtdown);
%plot((fx1(1:length(value0)))/1e6, value0);
plot( fx1/1e6, value0(1:length(fx1)));
xlabel('频率/MHz');

T = 10^(-5);
u = B / T;
c = 3e8;
fs = 25e6;
ts = 1 / fs;
t1 = 0 : ts : T-ts;
hdt = sin(2*pi*(0*t1+0.5*u*t1.^2));
figure;
plot(hdt);

replica = xrtdown;
y = fliplr(hdt);
% out = conv(replica, y);
replica1= [replica,zeros(1,16384-length(replica))];
y1 = [hdt,zeros(1,16384-length(hdt))];

rfft = fft(replica1);
yfft = fft(y1);
out = abs(ifft((rfft.*conj(yfft))));
figure;
t = (0:length(xrtdown)-1)*ts*c/2/1000;
plot(t, out(1:length(t)));
xlabel('距离/km');