决策树:ID3&C4.5&cart算法(从原理到实现-小白教程超详细)
文章目录
- 决策树
- ID3算法
- 信息熵
- 条件特征信息熵
- 信息增益
- ID3的缺陷
- C4.5算法
- 特征不确定性定量
- 信息增益率
- 小结
- cart算法
- 基尼系数
- 特征条件基尼系数
- 小结
决策树
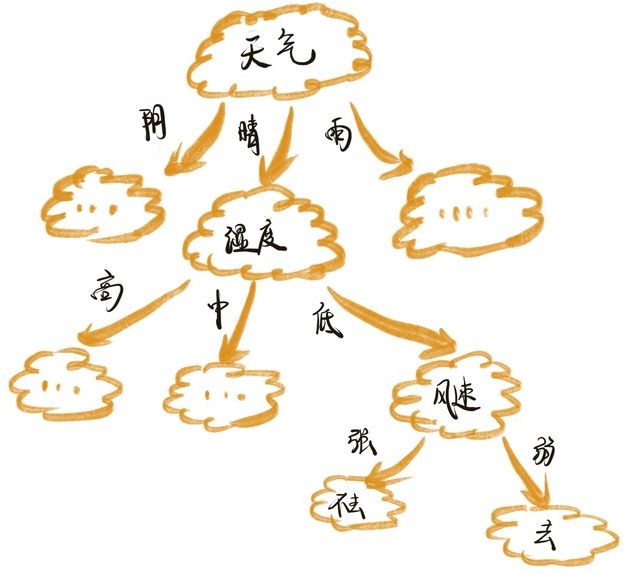
所谓决策树,就是一种树形结构的分类模型(也可以用作回归),它列举了每个特征下可能的情况以及对应情况下的下一步内容。下面是一个是否打篮球的决策树的例子:
小C:今天天气怎么样?
小P:晴
小C:温度呢?
小P:适中
小C:湿度呢?
小P:偏干燥,低
小C:风速如何?
小P:弱风
小C:好,那今天是个打篮球的好日子!
决策树的过程分两步,构建和决策(上述过程展示了如何决策)。构建的时候采用训练数据,带有所有特征和分类结果。决策的时候用测试数据,带有特征但无分类结果,通过决策得到分类结果。
ID3算法
ID3算法是决策树算法的一种,它采用信息增益的方式选择合适的属性作为划分属性。要理解ID3算法,需要先知道几个基本概念
信息熵
信息熵表示了信息的不确定度,是由信息学之父香农引入的。
什么是不确定度?其计算公式如下:
E n t r o p y ( T ) = − ∑ i = 1 n p ( i ∣ T ) l o g 2 p ( i ∣ T ) Entropy(T) = -\sum_{i=1}^n p(i|T)log_2p(i|T) Entropy(T)=−i=1∑np(i∣T)log2p(i∣T)
其中, i i i是可分类别,例如打篮球中可分类别就是是、否两类, p ( i ∣ T ) p(i|T) p(i∣T)表示类别 T T T分为 i i i类的概率。
还是以打篮球为例。下面是根据属性特征已有分类结果的表格:
| 天气 | 温度 | 湿度 | 风速 | 是否打篮球 |
|---|---|---|---|---|
| 晴 | 炎热 | 高 | 弱 | 否 |
| 晴 | 炎热 | 高 | 强 | 否 |
| 阴 | 炎热 | 高 | 弱 | 是 |
| 雨 | 适中 | 高 | 弱 | 是 |
| 雨 | 寒冷 | 中 | 弱 | 是 |
| 雨 | 寒冷 | 中 | 强 | 否 |
| 阴 | 寒冷 | 中 | 强 | 是 |
| 晴 | 适中 | 高 | 弱 | 否 |
| 晴 | 寒冷 | 中 | 弱 | 是 |
| 雨 | 适中 | 中 | 弱 | 是 |
| 晴 | 适中 | 中 | 强 | 是 |
| 阴 | 适中 | 高 | 强 | 是 |
| 阴 | 炎热 | 中 | 弱 | 是 |
| 雨 | 适中 | 高 | 强 | 否 |
以上述表格为例(9个是,5个否),是否打篮球的信息熵就是
E n t r o p y ( T ) = − 9 14 ∗ l o g 2 9 14 − 5 14 ∗ l o g 2 5 14 = 0.940 Entropy(T) =-\frac{9}{14}*log_2\frac{9}{14} -\frac{5}{14}*log_2\frac{5}{14} = 0.940 Entropy(T)=−149∗log2149−145∗log2145=0.940
从直观的角度理解,当分类种类越多,分类的数量越均匀,信息熵越高。即纯度越低,很高的信息熵会让我们在决策的时候更加难以判断分类结果,需要借助更多的其他条件来确定。
(是、是、是、否、否、否)要比(是、是、是、是、是、否)信息熵更大,因为前者更加混乱
信息熵度量了这个类别的混乱程度,如果一个信息熵很小的类别,如(是、是、是、是、是、是),那么根本不需要决策,无论什么条件下结果都是一样
条件特征信息熵
又叫条件属性信息熵,其表示在某种特征条件下,所有类别出现的不确定性之和。其实他就在信息熵的基础上添加了特征这一选项。其计算公式为
E n t r o p y ( T ∣ F ) = ∑ i = 1 n D i D ∗ E n t r o p y ( F i ) Entropy(T| F) = \sum_{i=1}^n\frac{D_i}{D}*Entropy(F_i) Entropy(T∣F)=i=1∑nDDi∗Entropy(Fi)
其中, D i D_i Di表示这种特征第i种情况的取值数,D表示这种特征所有的取值数, E n t r o p y ( F i ) Entropy(F_i) Entropy(Fi)是信息熵,不过此时计算的信息熵是限定在情况(例如晴)下的。直观的理解就是如果按照天气特征分类得到的加权不纯度(信息熵越高,样本越不纯)。
以上述表格的天气特征为例:
E n t r o p y ( T ∣ 天 气 ) = 5 14 ∗ [ − 2 5 ∗ l o g 2 2 5 − 3 5 ∗ l o g 2 3 5 ] + 4 14 ∗ [ − 4 4 ∗ l o g 2 4 4 ] + 5 14 ∗ [ − 3 5 ∗ l o g 2 3 5 − 2 5 ∗ l o g 2 2 5 ] = 0.694 Entropy(T|天气) = \frac{5}{14}*[-\frac{2}{5}*log_2\frac{2}{5} - \frac{3}{5}*log_2\frac{3}{5}] + \frac{4}{14}*[-\frac{4}{4}*log_2\frac{4}{4} ] + \frac{5}{14}*[-\frac{3}{5}*log_2\frac{3}{5} - \frac{2}{5}*log_2\frac{2}{5}] \\= 0.694 Entropy(T∣天气)=145∗[−52∗log252−53∗log253]+144∗[−44∗log244]+145∗[−53∗log253−52∗log252]=0.694
这里可能有点混乱,一开始我们求分类结果(是否打篮球)的信息熵,是为了得到当前数据的混乱程度(信息熵越高,数据越难划分)。而条件信息熵则是我们假设按照某一个特征(如天气)划分之后得到的新的加权(权重是特征中不同取值所占比例)混乱程度,一般情况新的加权混乱程度都是小于原始混乱程度的,即我们通过问了天气情况这个问题,使得数据更好划分了。下面的信息增益则是用于定量分析这个“更好划分”的程度。
信息增益
信息增益用直白的话来讲就是我选择这个信息分类,能带我多少分类收益(数据变得更好划分的程度)。它用于ID3中选择上层分类特征的基准,信息增益越高,则越要放到前面进行决策,因为很可能你根据这个很高的特征就可以直接进行分类,而不需要再考虑其他属性。
下面是一个信息增益对比的例子:
如果只要是晴天,我肯定去打球,只要是阴天和雨天,我肯定不去打球,这就导致我们可以直接通过天气进行分类,说明其信息增益很高。说到这,你也应该理解和分类结果越贴合的特征,其信息增益应该越高。
显然天气的信息增益要大于温度,对信息进行定量计算用以下公式:
G a i n ( F ) = E n t r o p y ( T ) − E n t r o p y ( T ∣ F ) Gain(F) = Entropy(T) - Entropy(T|F) Gain(F)=Entropy(T)−Entropy(T∣F)
以天气为例,天气这一特征的信息增益为
G a i n ( 天 气 ) = 0.940 − 0.694 = 0.246 Gain(天气) = 0.940 - 0.694 = 0.246 Gain(天气)=0.940−0.694=0.246
同理可得到 G a i n ( 温 度 ) = 0.029 Gain(温度) = 0.029 Gain(温度)=0.029, G a i n ( 湿 度 ) = 0.15 Gain(湿度) = 0.15 Gain(湿度)=0.15 G a i n ( 风 速 ) = 0.048 Gain(风速) = 0.048 Gain(风速)=0.048
由此可以知道天气的信息增益最大,在ID3算法中就将天气作为决策树的根节点,依据天气特征,将原来的表一分为三,如下:
- 表1(晴)
温度 湿度 风速 是否打篮球 炎热 高 弱 否 炎热 高 强 否 适中 高 弱 否 适中 高 弱 否 寒冷 中 弱 是 - 表2(阴)
温度 湿度 风速 是否打篮球 炎热 高 弱 是 寒冷 中 强 是 适中 高 强 是 炎热 中 弱 是 - 表3(雨)
温度 湿度 风速 是否打篮球 适中 高 弱 是 寒冷 中 弱 是 寒冷 中 强 否 适中 中 弱 是 适中 高 强 否
再对剩下的表格继续做重复操作。观察表格你可以发现按照天气分类后,决策结果纯度已经较高了。实际上,当天气为阴的时候决策树已经可以直接返回打篮球的结果了,所以阴的下一节点是叶节点(是)。
我们继续对晴和雨进行信息增益计算,添加新特征到决策树操作。可以进一步将决策树划分为以下:
-
表4(晴-湿度高)
温度 湿度 风速 是否打篮球 炎热 高 弱 否 炎热 高 强 否 适中 高 弱 否 适中 高 弱 否 -
表5(晴-湿度中)
温度 湿度 风速 是否打篮球 寒冷 中 弱 是 -
表6(雨-风强)
温度 湿度 风速 是否打篮球 寒冷 中 强 否 适中 高 强 否 -
表7(雨-风弱)
温度 湿度 风速 是否打篮球 适中 高 弱 是 寒冷 中 弱 是 适中 中 弱 是
当预测一条新的数据时,我们只需要从天气特征开始,依次往下判断即可。
例如[晴,炎热,高,强], 天气 -> 晴 ->湿度 -> 高->否 ,即不去打球
ID3的缺陷
ID3算法只考虑了信息增益,但却忽视了特征本身不确定性就可能很大的问题,这就好比只拿全国GDP跟人家比,却不考虑人均GDP,在特征情况数相差不大的情况下,对ID3算法的影响不大,可一旦特征本身可能情况就很多,就会导致训练的决策树算法不佳。
举一个很直观的极端例子,一个拥有10种的情况的特征,其情况1与分类1对应,其余9种和分类2对应,在用该特征进行划分后,对于分类帮助并不是很大,因为你还要从9种特征中再依据其他条件细分。
C4.5算法
C4.5算法可看做ID3算法的升级版,它考虑了ID3算法中仅用信息增益的不足,引入了信息增益率的概念。
特征不确定性定量
前面说过,虽然信息增益很高,但是特征的情况数很多(即特征的混乱度也很高)的时候,会影响决策树的效果,因此我们就需要计算特征本身的信息熵用以度量该特征的不确定性。
计算特征不确定性的公式就是信息熵的公式,可以得到
U n c e r t a i n ( 天 气 ) = − 5 14 ∗ l o g 2 5 14 − 5 14 ∗ l o g 2 5 14 − 4 14 ∗ l o g 2 4 14 = 1.577 Uncertain(天气) = -\frac{5}{14}*log_2\frac{5}{14} - \frac{5}{14}*log_2\frac{5}{14} - \frac{4}{14}*log_2\frac{4}{14} = 1.577 Uncertain(天气)=−145∗log2145−145∗log2145−144∗log2144=1.577
U n c e r t a i n ( 温 度 ) = − 4 14 ∗ l o g 2 4 14 − 6 14 ∗ l o g 2 6 14 − 4 14 ∗ l o g 2 4 14 = 1.556 Uncertain(温度) = -\frac{4}{14}*log_2\frac{4}{14} - \frac{6}{14}*log_2\frac{6}{14} - \frac{4}{14}*log_2\frac{4}{14} = 1.556 Uncertain(温度)=−144∗log2144−146∗log2146−144∗log2144=1.556
U n c e r t a i n ( 湿 度 ) = − 7 14 ∗ l o g 2 7 14 − 7 14 ∗ l o g 2 7 14 = 1.0 Uncertain(湿度) = -\frac{7}{14}*log_2\frac{7}{14} - \frac{7}{14}*log_2\frac{7}{14} = 1.0 Uncertain(湿度)=−147∗log2147−147∗log2147=1.0
U n c e r t a i n ( 风 速 ) = − 6 14 ∗ l o g 2 6 14 − 8 14 ∗ l o g 2 8 14 = 0.985 Uncertain(风速) = -\frac{6}{14}*log_2\frac{6}{14} - \frac{8}{14}*log_2\frac{8}{14} = 0.985 Uncertain(风速)=−146∗log2146−148∗log2148=0.985
信息增益率
信息增益率为
I G R ( F ) = G a i n ( F ) / U n c e r t a i n ( F ) IGR(F) = Gain(F) / Uncertain(F) IGR(F)=Gain(F)/Uncertain(F)
由此得到
I G R ( 天 气 ) = G a i n ( 天 气 ) / U n c e r t a i n ( 天 气 ) = 0.246 / 1.577 = 0.155 IGR(天气) = Gain(天气) / Uncertain(天气) = 0.246 / 1.577 = 0.155 IGR(天气)=Gain(天气)/Uncertain(天气)=0.246/1.577=0.155
I G R ( 温 度 ) = G a i n ( 温 度 ) / U n c e r t a i n ( 温 度 ) = 0.029 / 1.556 = 0.0186 IGR(温度) = Gain(温度) / Uncertain(温度) = 0.029/ 1.556 = 0.0186 IGR(温度)=Gain(温度)/Uncertain(温度)=0.029/1.556=0.0186
I G R ( 湿 度 ) = G a i n ( 温 度 ) / U n c e r t a i n ( 温 度 ) = 0.151 / 1.0 = 0.151 IGR(湿度) = Gain(温度) / Uncertain(温度) = 0.151/ 1.0 = 0.151 IGR(湿度)=Gain(温度)/Uncertain(温度)=0.151/1.0=0.151
I G R ( 风 速 ) = G a i n ( 风 速 ) / U n c e r t a i n ( 风 速 ) = 0.048 / 0.985 = 0.049 IGR(风速) = Gain(风速) / Uncertain(风速) = 0.048 / 0.985= 0.049 IGR(风速)=Gain(风速)/Uncertain(风速)=0.048/0.985=0.049
接下来的步骤只需要将ID3中的信息增益作为基准的地方用信息增益率替换即可。
小结
总结一下ID3,C4.5算法的算法步骤,可以用下面的流程图表示:
流程图中的节点是指用于划分的数据
<即是否全为同一类>
选出最大者,用其划分数据
结果,将该分类特征情况去除
进行划分的节点
cart算法
cart算法也是应用决策树的算法之一,再一次理解决策树的核心是将混杂的数据划分成纯净的数据,划分的依据在于特征的选择。因此怎么评价一个特征是不是一个好特征,是通过其划分的数据“纯度”得到的。而评价的定量标准在ID3中是信息增益,在C4.5中是信息增益率,在cart中是基尼系数。
基尼系数
基尼系数反映了样本的不确定度,样本差异越小,基尼系数越小;反之,基尼系数越大。我们常用基尼系数衡量一个国家收入差距。先来看看基尼系数的计算公式:
G i n i ( T ) = 1 − ∑ k = 1 n [ p ( T k ∣ T ) ] 2 Gini(T) = 1 - \sum_{k=1}^n[p(T_k|T)]^2 Gini(T)=1−k=1∑n[p(Tk∣T)]2
其中, T T T代表分类(如是否去打篮球), T k T_k Tk代表第k个分类情况(在打篮球中就是:是/否 ),我们以之前打篮球的例子的一部分来做示例计算。
| 温度 | 湿度 | 风速 | 是否打篮球 |
|---|---|---|---|
| 适中 | 高 | 弱 | 是 |
| 寒冷 | 中 | 弱 | 是 |
| 寒冷 | 中 | 强 | 否 |
| 适中 | 中 | 弱 | 是 |
| 适中 | 高 | 强 | 否 |
查看是否打篮球分类列,包含 {是,是,是,否,否}5个结果。其 G i n i Gini Gini系数为:
G i n i ( T ) = 1 − [ ( 3 5 ) 2 + ( 2 5 ) 2 ] = 0.48 Gini(T) = 1 - [(\frac{3}{5})^2+(\frac{2}{5})^2] = 0.48 Gini(T)=1−[(53)2+(52)2]=0.48
特征条件基尼系数
与ID3中的特征条件信息熵类似,它反映的是利用特征进行数据划分后,分类基尼系数的变化情况。下面是其计算公式:
G i n i ( T , F ) = ∑ i = 1 2 D i D ∗ G i n i ( T i ) Gini(T,F) = \sum_{i=1}^2\frac{D_i}{D}*Gini(T_i) Gini(T,F)=i=1∑2DDi∗Gini(Ti)
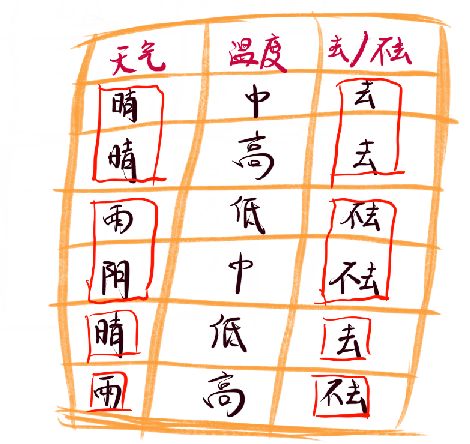
D i D_i Di是分类结果某一类中的样本数量, D D D是总的样本数量。为什么累加是2不是n?注意cart算法和ID3、C4.5算法有一个不同点是cart算法构造的是二叉树,更加简洁,针对一个特征的一个具体情况(例如湿度:高),cart在分类的时候会将样本分为高和不高两类,所以公式中的集合总是2个。分成二叉树的好处是结构更为简单。下面是我绘制的一个样例:

分别按湿度的高、不高,风速的强、不强两种特征划分得到基尼系数显然用风速的强、不强划分要更好,因为其基尼系数更小。(基尼系数为0说明完成了纯净划分)。此时就完成了一次划分,对划分的结果进行判断是否分类已经“纯”了,若不纯,则继续划分。
小结
总结一下cart算法的流程。
流程图中的节点是指用于划分的数据
情况的条件基尼系数
将该分类特征情况去除
进行划分的节点
决策树的这几个算法本身并不难理解,但仍需要自己多动手在纸上运算才能深入理解。如果想要将其应用到实际开发中,建议自己动手实现一下。如果觉得有难度,也没有关系,我已经将对应算法的代码放在了我的Github中,你可以对照参考。