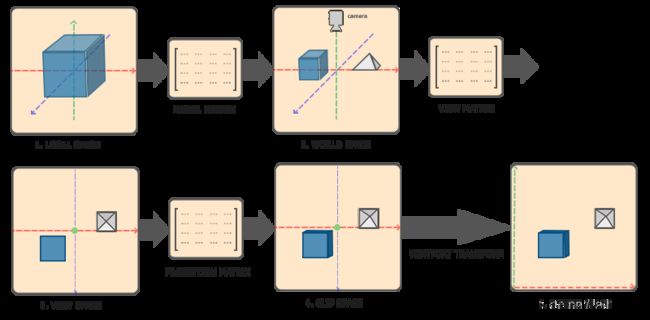
OpenGL基础11：空间

 

一、局部空间

即对象被创建时，所在的空间

例如我们用模型软建（ZBrush、Blender、3DMax等）创建了一条龙的模型，那么它在创建的时候，就处于它的局部空间内，一般来讲，模型的中心即局部空间的中心(0, 0, 0)，如果我们这里说龙的眼睛的坐标为(2.2, 1.5, -2)，那么也就是这个龙的眼睛相对于自身的中心，偏移量为(2.2, 1.5, -2)

 

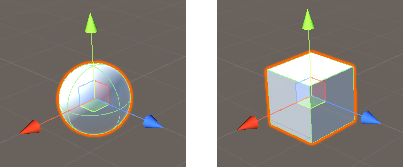
就如下图，一个球体和一个正方体，它们都处于各自的局部空间，并且中心都在(0, 0, 0)的位置

 

二、世界空间

如果我们将所有的对象导入到程序当中，它们就有可能全部挤在世界的原点上(0, 0, 0)，然而这并不是我们想要的结果，我们想要为每一个对象分配一个合理的位置，世界坐标即是如此

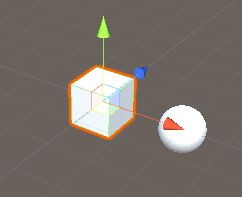
如下图，我们为正方形分配了一个坐标(0, 0, 0)，球体分配了一个坐标(2, 0, 0)

那么上面的坐标(2, 0, 0)和(0, 0, 0)就是物体相对于（游戏）世界的位置

• 我们一般所说的坐标，往往都默认是世界坐标

对象的坐标通过模型矩阵(Model Matrix)，来完成局部坐标到世界坐标的转换的，还记得上一章所说的位移、缩放、旋转矩阵嘛，这里的模型矩阵也可以说是一种转换矩阵

 

三、观察空间

在现实世界中，观察空间即我们眼睛所看到的空间，也就是视觉空间

在游戏世界中，观察空间即摄像机所监视的空间，也就是摄像机空间

很明显无论是摄像机还是我们的眼睛，本质都是将对象的世界空间的坐标转换为观察者视野前面的坐标，也可以这样理解，游戏世界中的摄像机 = 我们的眼睛

 

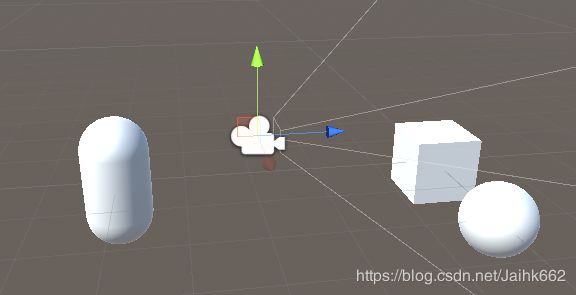
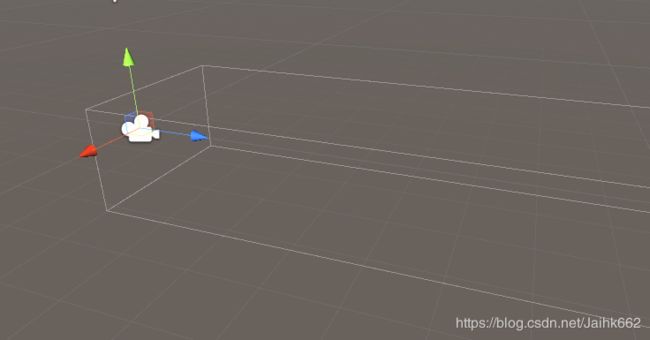
如下，世界中有3个物体，但只有正方形和球在摄像机的范围内，图2就是观察空间

世界空间到观察空间的变换就相对复杂一点，通常是由一系列的平移和旋转的组合来平移和旋转场景从而使得特定的对象被转换到摄像机前面，这些组合在一起的转换通常存储在一个观察矩阵(View Matrix)里，用来将世界坐标转换到观察空间

 

四、裁剪空间

在一个顶点着色器运行的最后，所有的坐标应该都在一个给定的范围内，这部分的坐标将变为屏幕上可见的片段，这个范围即是裁剪空间(Clip Space)，任何在这个范围之外的点都会被裁剪掉(Clipped)，也就是被忽略

为了将顶点坐标从观察空间转换到裁剪空间，我们需要用到投影矩阵

投影矩阵首先会将所有顶点坐标从观察空间变换到裁剪空间，然后，这些顶点会被再次变换到标准化设备坐标(normalized device coordinates/ NDC space)，即(-1, 1)这个范围，所有在在范围(-1, 1)外的坐标都不会被绘制出来并且会被裁剪，这一步是通过用用裁剪坐标的分量除裁剪坐标实现的，这个操作被称为透视划分(Perspective Division)，在透视划分之后，就没有w这一分量了

• 如果只是片段的一部分例如三角形超出了裁剪体积(Clipping Volume)，则OpenGL会重新构建三角形以使一个或多个三角形能适应在裁剪范围内

正射投影和透视投影

再回到摄像机，可以从上面的图中看出，摄像机前有一个白线范围，这便是由投影矩阵创建的观察区域(Viewing Box)，也被称为平截头体(Frustum)，很显然，每个出现在平截头体范围内的坐标都会最终出现在用户的屏幕上

投影矩阵将观察坐标转换为裁剪坐标的过程有两种不同的方式（通过不同的投影矩阵），分别为正射投影(Orthographic Projection)和透视投影(Perspective Projection)，如下：

正射投影异常的简单，其平截头体就是一个标准的立方体

透视投影的平截头体是个锥体，这也是现实生活中，人眼睛的视线范围，在这种投影方式下，同样的物体离摄像头（眼睛）越近，它就会显得越大，这种效果也被叫做为透视(Perspective)

关于投影矩阵的计算可以参考这篇文章：中文版、原文

可以利用glm直接生成对应的投影矩阵：

• glm::ortho(l, r, x, y, A, B)：创建一个正射投影矩阵，第1~2个参数指定了平截头体的左右坐标，第3~4参数指定了平截头体的底部和上部坐标，通过这四个参数我们定义了近平面和远平面的大小，第5~6参数为近平面和远平面的距离，刚好这6个参数制定了一块立方体区域
• glm::perspective(, p, A, B)：创建一个透视投影矩阵，第1个参数为视锥体的开放角度，也被称为视野(Field of View)，对于一个真实的观察效果，它的值一般默认都是45°，第2个参数为宽高比，由视口的高除以宽(width/height)，第3~4个参数设置了平截头体的近和远平面，一般默认设置近距离为0.1而远距离设为100，所有在近平面和远平面的顶点且处于平截头体内的顶点都会被渲染。

 

五、屏幕空间

可以看出来，这也是一条坐标变换的流水线，我们将所有顶点转换为片段之前，顶点会处于的不同的状态空间中

整合的最终公式为：

经过上面的计算后，顶点就会被赋予顶点着色器中的gl_Position并且OpenGL将会对其自动进行透视划分和裁剪，并在完成后映射到屏幕空间(由glViewport设置)且被转换成片段，在此每个坐标都会关联着一个屏幕上的点（像我们平时的2k屏就是2560 * 1440)