分类——决策树算法(Python3实现)
决策树算法的核心思想:根据特征以及其对应特征值组成的元组为切点切分样本空间;
决策树算法是分类算法中的一种,ID3及C4.5决策树是多叉树。
1.熵、条件熵与信息增益
-
熵(entropy)
在信息论与概率统计中,熵(entropy)是表示随机变量不确定性的度量。X为有限个值的离散随机变量,其概率分布为:
![]()
则随机变量X的熵可以定义为:
-
条件熵(condition entropy)
设有随机变量(X,Y),其联合概率分布为
![]()
条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。随机变量X给定的条件下,随机变量Y的条件熵,定义为X给定条件下Y的条件概率分布的熵对X的数学期望:
![]()
实际计算,就是根据特征Y的取值将数据集划分成若干子数据集,分别计算子数据集的熵,然后以子数据集占比为权重求平均值。
-
信息增益(information gain)
表示得知特征X的信息而使得类Y的信息不确定性减少的程度。
特征A对训练数据集D的信息增益g(D,X),定义为集合D的经验熵H(D)与特征X给定条件下D的经验熵H(D|X)之差,
![]()
由公式可知,计算条件熵时,特征X若取值较多,那么数据划分更细,则条件熵偏向于减小,极端情况下,每个样本都是独一无二的,那么条件熵为0。信息增益就偏向于取值多的特征,进行更多的划分,故引进信息增益比。
2.信息增益算法流程
根据信息增益准则的特征选择方法是:对训练数据集(或子集)D,计算其每个特征的信息增益,并比较它们的大小,选择信息增益最大的特征。
设训练数据集为D,|D|表示其样本容量,即样本个数。设有K个类![]() ,
,![]() ,
,![]() 为属于
为属于![]() 的样本个数,
的样本个数,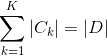 。设特征X有n个不同的取值
。设特征X有n个不同的取值![]() ,根据特征X的取值将D划分为n个子集
,根据特征X的取值将D划分为n个子集![]() ,其中
,其中![]() 为
为![]() 的样本个数,
的样本个数,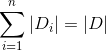 。即子集
。即子集![]() 中属于类
中属于类![]() 的样本的集合为
的样本的集合为![]() ,即
,即![]() ,
,![]() 为
为![]() 的样本个数。于是信息增益的算法如下:
的样本个数。于是信息增益的算法如下:
(1)计算数据集D的经验熵H(D)
(2)计算特征X对数据集D的经验条件熵H(D|A)
(3)计算信息增益
![]()
3.数据集及计算每个特征的信息增益
- 样本数据表
| 1 | 青年 | 否 | 否 | 一般 | 否 |
| 2 | 青年 | 否 | 否 | 好 | 否 |
| 3 | 青年 | 是 | 否 | 好 | 是 |
| 4 | 青年 | 是 | 是 | 一般 | 是 |
| 5 | 青年 | 否 | 否 | 一般 | 否 |
| 6 | 中年 | 否 | 否 | 一般 | 否 |
| 7 | 中年 | 否 | 否 | 好 | 否 |
| 8 | 中年 | 是 | 是 | 好 | 是 |
| 9 | 中年 | 否 | 是 | 非常好 | 是 |
| 10 | 中年 | 否 | 是 | 非常好 | 是 |
| 11 | 老年 | 否 | 是 | 非常好 | 是 |
| 12 | 老年 | 否 | 是 | 好 | 是 |
| 13 | 老年 | 是 | 否 | 好 | 是 |
| 14 | 老年 | 是 | 否 | 非常好 | 是 |
| 15 | 老年 | 否 | 否 | 一般 | 否 |
- 根据信息增益准则选择最优特征
对于所给的训练数据集D,先计算经验熵H(D)。
然后计算各特征对数据集D的信息增益,分别以![]() 表示年龄、有工作、有自己的房子和信贷情况4个特征,则
表示年龄、有工作、有自己的房子和信贷情况4个特征,则
(1)
这里![]() 分别是D中
分别是D中![]() (年龄)取值为青年、中年和老年的样本子集,类似地,
(年龄)取值为青年、中年和老年的样本子集,类似地,
(2)
(3)
(4)
![]()
最后,比较各特征的信息增益值。由于特征![]() (有自己的房子)的信息增益值最大,所以选择特征
(有自己的房子)的信息增益值最大,所以选择特征![]() 作为最优特征。
作为最优特征。
4.信息增益比(information gain ratio)
其中,n就是特征X不同取值的个数,也即子数据集的个数。分母是数据集自身划分引起的熵变。显然,划分越多,熵越大。
优点:
-
容易理解,可视化。模型是“白箱”
-
无需过多的数据准备
-
预测过程时间复杂度为log(n)
-
能够处理连续以及离散值
缺点:
-
容易过拟合。可通过剪枝等方法减轻
-
稳定性差。可通过集成学习改进
-
学习过程是一个NP完全问题
-
模型不能表示XOR等概念
-
对类不平衡样本集敏感
5.算法流程
input:阈值epsilon,训练数据集X,y
output:决策树
Step1:初始化,构建特征集及空树
Step2:递归构建决策树
参数:特征集,子训练数据集X_data,y_data
递归终止条件:
1.集只有一个类,返回该类
2.特征集为空,返回最频繁的类
3.切分数据集前后,信息增益(比)小于epsilon
树的构建流程:
1.计算每个特征的信息增益(比),以及切分的子数据集的索引
2.选取信息增益(比)最大的特征为最优特征,构建当前节点
3.从特征集中去除当前最优特征,并对相应的子数据集分别进行步骤1、步骤2构建子树
Step3:运用构建好的决策树进行预测。递归搜素树,碰到叶节点则返回类标记
6.Python3代码实现
import math
from collections import Counter, defaultdict
import numpy as np
class node:
# 这里构建树的节点类,也可用字典来表示树结构
def __init__(self, fea=-1, res=None, child=None):
self.fea = fea
self.res = res
self.child = child # 特征的每个值对应一颗子树,特征值为键,相应子树为值
class DecisionTree:
def __init__(self, epsilon=1e-3, metric='C4.5'):
self.epsilon = epsilon
self.tree = None
self.metric = metric
def exp_ent(self, y_data):
# 计算经验熵
c = Counter(y_data) # 统计各个类标记的个数
ent = 0
N = len(y_data)
for val in c.values():
p = val / N
ent += -p * math.log2(p)
return ent
def con_ent(self, fea, X_data, y_data):
# 计算条件熵并返回,同时返回切分后的各个子数据集
fea_val_unique = Counter(X_data[:, fea])
subdata_inds = defaultdict(list) # 根据特征fea下的值切分数据集
for ind, sample in enumerate(X_data):
subdata_inds[sample[fea]].append(ind) # 挑选某个值对应的所有样本点的索引
ent = 0
N = len(y_data)
for key, val in fea_val_unique.items():
pi = val / N
ent += pi * self.exp_ent(y_data[subdata_inds[key]])
return ent, subdata_inds
def infoGain(self, fea, X_data, y_data):
# 计算信息增益
exp_ent = self.exp_ent(y_data)
con_ent, subdata_inds = self.con_ent(fea, X_data, y_data)
return exp_ent - con_ent, subdata_inds
def infoGainRatio(self, fea, X_data, y_data):
# 计算信息增益比
g, subdata_inds = self.infoGain(fea, X_data, y_data)
N = len(y_data)
split_info = 0
for val in subdata_inds.values():
p = len(val) / N
split_info -= p * math.log2(p)
return g / split_info, subdata_inds
def bestfea(self, fea_list, X_data, y_data):
# 获取最优切分特征、相应的信息增益(比)以及切分后的子数据集
score_func = self.infoGainRatio
if self.metric == 'ID3':
score_func = self.infoGain
bestfea = fea_list[0] # 初始化最优特征
gmax, bestsubdata_inds = score_func(bestfea, X_data, y_data) # 初始化最大信息增益及切分后的子数据集
for fea in fea_list[1:]:
g, subdata_inds = score_func(fea, X_data, y_data)
if g > gmax:
bestfea = fea
bestsubdata_inds = subdata_inds
gmax = g
return gmax, bestfea, bestsubdata_inds
def buildTree(self, fea_list, X_data, y_data):
# 递归构建树
label_unique = np.unique(y_data)
if label_unique.shape[0] == 1: # 数据集只有一个类,直接返回该类
return node(res=label_unique[0])
if not fea_list:
return node(res=Counter(y_data).most_common(1)[0][0])
gmax, bestfea, bestsubdata_inds = self.bestfea(fea_list, X_data, y_data)
if gmax < self.epsilon: # 信息增益比小于阈值,返回数据集中出现最多的类
return node(res=Counter(y_data).most_common(1)[0][0])
else:
fea_list.remove(bestfea)
child = {}
for key, val in bestsubdata_inds.items():
child[key] = self.buildTree(fea_list, X_data[val], y_data[val])
return node(fea=bestfea, child=child)
def fit(self, X_data, y_data):
fea_list = list(range(X_data.shape[1]))
self.tree = self.buildTree(fea_list, X_data, y_data)
return
def predict(self, X):
def helper(X, tree):
if tree.res is not None: # 表明到达叶节点
return tree.res
else:
try:
sub_tree = tree.child[X[tree.fea]]
return helper(X, sub_tree) # 根据对应特征下的值返回相应的子树
except:
print('input data is out of scope')
return helper(X, self.tree)
def validate(X_data, y_data, ratio=0.15):
N = X_data.shape[0]
size = int(N * ratio)
inds = np.random.permutation(range(N))
for i in range(int(N / size)):
test_ind = inds[i * size:(i + 1) * size]
train_ind = list(set(range(N))-set(test_ind))
yield X_data[train_ind], y_data[train_ind], X_data[test_ind], y_data[test_ind]
if __name__ == '__main__':
import time
start = time.clock()
data = np.array([['青年', '青年', '青年', '青年', '青年', '中年', '中年',
'中年', '中年', '中年', '老年', '老年', '老年', '老年', '老年'],
['否', '否', '是', '是', '否', '否', '否', '是', '否',
'否', '否', '否', '是', '是', '否'],
['否', '否', '否', '是', '否', '否', '否', '是',
'是', '是', '是', '是', '否', '否', '否'],
['一般', '好', '好', '一般', '一般', '一般', '好', '好',
'非常好', '非常好', '非常好', '好', '好', '非常好', '一般'],
['否', '否', '是', '是', '否', '否', '否', '是', '是',
'是', '是', '是', '是', '是', '否']])
data = data.T
X_data = data[:, :-1]
y_data = data[:, -1]
g = validate(X_data, y_data, ratio=0.2)
for item in g:
X_data_train, y_data_train, X_data_test, y_data_test = item
clf = DecisionTree()
clf.fit(X_data_train, y_data_train)
score = 0
for X, y in zip(X_data_test,y_data_test):
if clf.predict(X) == y:
score += 1
print(score / len(y_data_test))
print(time.clock() - start)
![]()
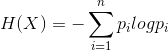


![g(D,A_{3})=0.971-\left [ \frac{6}{15}\times 0+ \frac{9}{15}\left ( - \frac{3}{9}log_{2}\frac{3}{9}- \frac{6}{9}log_{2}\frac{6}{9}\right ) \right ]\\ =0.971-0.551=0.420](http://img.e-com-net.com/image/info8/94f2be74eccc487f955672905fa70977.gif)
