（信贷风控十二）GBDT模型用于评分卡模型（理论）

GBDT模型用于评分卡模型

本文主要总结以下内容：

• GBDT模型基本理论介绍
• GBDT模型如何调参数
• GBDT模型对样本违约概率进行估计（GBDT模型用于评分卡python代码实现请看下一篇博客）
• GBDT模型挑选变量重要性
• GBDT模型如何进行变量的衍生

 

GBDT模型基本理论介绍

GBDT(Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree)，是一种迭代的决策树算法，该算法由多棵决策树组成，所有树的结论累加起来做最终答案。它在被提出之初就和SVM一起被认为是泛化能力较强的算法。GBDT中的树是回归树（不是分类树），GBDT用来做回归预测，调整后也可以用于分类。

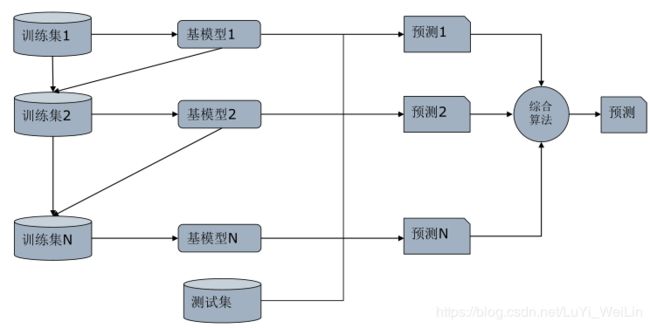
GBDT模型是集成学习框架Boosting的一种

一句话解释版本：

Bagging是决策树的改进版本，通过拟合很多决策树来实现降低方差

随机森林（Random Forrest）是Bagging的改进版本，通过限制节点可选特征范围优化Bagging

Boosting是Bagging的改进版本，通过吸取之前树的经验建立后续树优化Bagging
 

Boosting模型工作原理

• GBDT模型的原理

Y标签类别可以是（连续型[基模型：回归]、离散无序型[基模型：分类]、离散有序型[基模型：排序]）

不同的Y标签类型选择不一样的损失函数，上式中损失函数L(F(X),Y),其中Y是固定的，F(X)的针对不同问题，函数结构也是可以定下来的，唯一要确定的是函数所对应的参数使得该损失函数最小，所以我们把问题从函数空间搜索问题转换为参数空间搜索问题

• 常见的损失函数（针对不同Y标签类型选择不一样的损失函数）

Y标签类别可以是（连续型[基模型：回归]、离散无序型[基模型：分类]、离散有序型[基模型：排序]）

下面三个分别对应：回归型损失函数、分类型损失函数、逻辑回归损失函数（当然了这里只是举了常见的三个，比如回归型损失函数我们也可以使用均方差等损失函数，这里不过多去展开）

• 针对GBDT模型我们如何寻找最优参数呢？

运用最优化的思想，采用迭代的方法求出其参数（因为现实中是很难求其精确解的，就算可以求解也要花费大量的时间，我们可以问题简化，求出P的近似解即可，无限的逼近到一个我们可以接受的范围即可），如何迭代呢？我们先了解一下梯度法

• 梯度法

• 梯度提升法

可能看到这里有的小伙伴已经云里雾里了，说的是什么呢？不急我们先来引用一下别人的例子（https://blog.csdn.net/zhangbaoanhadoop/article/details/81840669文章不错，建议大家去看一下）

---------------------------------------------------------------------------------------------------------------------------------------------------------------------

让损失函数沿着梯度方向的下降。这个就是gbdt 的 gb的核心。gbdt 每轮迭代的时候，都去拟合损失函数在当前模型下的负梯度。（如果损失函数使用的是平方误差损失函数，则这个损失函数的负梯度就可以用残差来代替，以下所说的残差拟合，便是使用了平方误差损失函数）

Boosting，迭代，即通过迭代多棵树来共同决策。这怎么实现呢？难道是每棵树独立训练一遍，比如A这个人，第一棵树认为是10岁，第二棵树认为是0岁，第三棵树认为是20岁，我们就取平均值10岁做最终结论？--当然不是！且不说这是投票方法并不是GBDT，只要训练集不变，独立训练三次的三棵树必定完全相同，这样做完全没有意义。之前说过，GBDT是把所有树的结论累加起来做最终结论的，所以可以想到每棵树的结论并不是年龄本身，而是年龄的一个累加量。GBDT的核心就在于，每一棵树学的是之前所有树结论和的残差，这个残差就是一个加预测值后能得真实值的累加量。比如A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学。

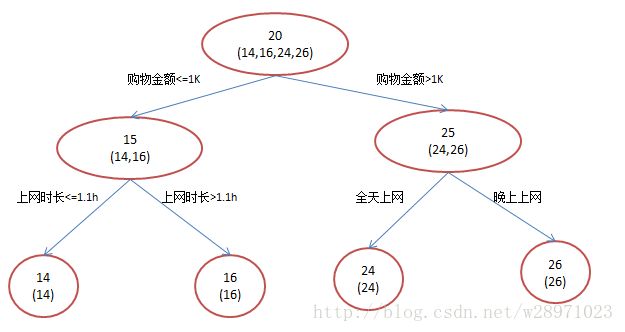
还是年龄预测，简单起见训练集只有4个人，A,B,C,D，他们的年龄分别是14,16,24,26。其中A、B分别是高一和高三学生；C,D分别是应届毕业生和工作两年的员工。如果是用一棵传统的回归决策树来训练，会得到如下图2所示结果：

图2：传统回归决策树

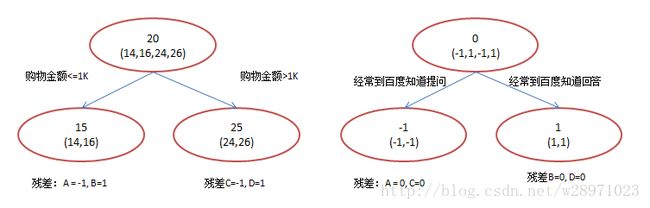
现在我们使用GBDT来做这件事，由于数据太少，我们限定叶子节点做多有两个，即每棵树都只有一个分枝，并且限定只学两棵树。我们会得到如下图3所示结果：

图3：GBDT模型

在第一棵树分枝和图2一样，由于A,B年龄较为相近，C,D年龄较为相近，他们被分为两拨，每拨用平均年龄作为预测值。此时计算残差（残差的意思就是： A的预测值 + A的残差 = A的实际值），所以A的残差就是16-15=1（注意，A的预测值是指前面所有树累加的和，这里前面只有一棵树所以直接是15，如果还有树则需要都累加起来作为A的预测值）。进而得到A,B,C,D的残差分别为-1,1，-1,1。然后我们拿残差替代A,B,C,D的原值，到第二棵树去学习，如果我们的预测值和它们的残差相等，则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了。这里的数据显然是我可以做的，第二棵树只有两个值1和-1，直接分成两个节点。此时所有人的残差都是0，即每个人都得到了真实的预测值。

换句话说，现在A,B,C,D的预测值都和真实年龄一致了。Perfect!：

A: 14岁高一学生，购物较少，经常问学长问题；预测年龄A = 15 – 1 = 14

B: 16岁高三学生；购物较少，经常被学弟问问题；预测年龄B = 15 + 1 = 16

C: 24岁应届毕业生；购物较多，经常问师兄问题；预测年龄C = 25 – 1 = 24

D: 26岁工作两年员工；购物较多，经常被师弟问问题；预测年龄D = 25 + 1 = 26 

-------------------------------------------------------------------------------------------------------------------------------------------------------------------------

看完例子，想必大家已经基本了解GBDT的原理了，那我们下面看梯度提升法在不同损失函数用法

把梯度提升法的思想带入逻辑回归损失函数

把梯度提升法的思想带入分类类型的损失函数

 

GBDT模型如何调整参数

GBDT该调整哪些参数

一般集成模型的参数分为两种类别：

• 框架层面参数
• 基模型层面参数

当然啦，GBDT模型框架层面参数和基模型层面参数是有非常多参数的，经验得出我们只需要关注以下几个变量即可（当然，特殊情况特殊处理）

• 框架层面参数

• 基模型层面参数

如何进行参数调节

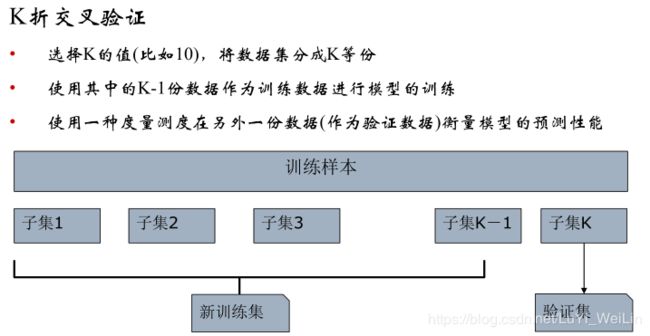
我们使用到的方法是：K折交叉验证（CV）

 

其优缺点：

 

基于k折交叉验证的网格搜索法（GridSearchCV）

每变一个参数，模型都要拟合一遍，大样本就会很卡。使用贪心算法，把n1*n2*n3*n4*......*nk复杂度变为n1+n2+n3+n4+......+nk，求其次优解。按照变量（框架层面参数、基模型层面参数）的重要程度来顺序调参。

 

GBDT模型对样本违约概率进行估计

代码请看下一篇博客

 

GBDT模型挑选变量重要性

集成模型几乎都能给出变量重要性的估计，因为有抽样成分在里面

 

GBDT模型如何进行变量的衍生

独热编码

在讲解变量衍生之前我们来了解一下独热编码（引用一下别人的博客介绍一下独热编码）

----------------------------------------------------------------------------------------------

原文：https://blog.csdn.net/windowsyun/article/details/78277880 

简单介绍
有一组数据，其中有个特征是性别。既然是性别，那它的值显然只有两个选择，要么男性（用1表示）要么女性（用0表示）。 
独热编码就是将这一个特征变成两个特征：是男性、是女性。 
我是男的，我的特征就变成了 [1, 0]，1代表我是男的，0代表我不是女的。同样，女性的特征变为[0, 1]。

用处
为什么用独热编码？ 
假设一个特征是颜色，选项有：黄色、红色、绿色等等。如果我们不采用独热编码，用0表示黄色，用1表示绿色，用2表示红色，以此类推。从数学上看，它们之间的距离不一样了，0和1的距离显然比0和2的距离小，可是不能认为黄色与红色的关系比绿色更接近。 
采用独热编码后，黄色变成[1, 0, 0 , … ]，红色变成[0, 1, 0, … ]，绿色变成[0, 0, 1, … ]，这样它们的相似度就一样了，这对机器学习算法很重要。
---------------------------------------------------------------------------------------

独热编码注意事项

 

变量衍生