SPSS（十一）SPSS信息浓缩技术--主成分分析、因子分析（图文+数据集）

SPSS（十一）信息浓缩技术--主成分分析、因子分析（图文+数据集）

当我们的自变量存在多重共线性，表现为进行回归时候方程系数估计不正常以及方程检验结果不正常，也许我们可以使用变量挑选的办法（手动挑选、向前法、向后法、逐步法），但是再复杂一点其实就不行了，之前我们介绍过岭回归解决该问题，其实我们还可以使用信息浓缩的技术来解决自变量存在多重共线性问题。

本讲课程中涉及的方法其实质均为数据化简、信息浓缩，即将分散在多个变量中的同类信息集中、提纯，从而便于分析、解释和利用。目的为浓缩信息（主成分分析）、目的为探讨内在结构（因子分析），正因如此，这些信息浓缩方法、特别是其中的因子分析方法，往往成为更复杂的多元分析方法的基石

主成分分析和因子分析都是对连续型的自变量进行信息浓缩，后面会讲解对分类自变量进行信息浓缩的方法--对应分析

• 主成分分析：解决变量间多重共线性(data reduction)

有太多的变量，希望能够消减变量，用一个新的、更小的由原始变量集组合成的新变量集作进一步分析

新变量集能够更有利于简化和解释问题

• 因子分析：探讨变量内在联系和结构(structure detection)

观测变量之间的存在相互依赖关系

 

主成分分析

只是一种中间手段，其背景是研究中经常会遇到多指标的问题，这些指标间往往存在一定的相关，直接纳入分析不仅复杂，变量间难以取舍，而且可能因多重共线性而无法得出正确结论

主成分分析的目的就是通过线性变换，将原来的多个指标组合成相互独立的少数几个能充分反映总体信息的指标（这些指标不一定会有准确的含义），便于进一步分析，尽可能保留原始变量的信息，且彼此不相关

在主成分分析中，提取出的每个主成分都是原来多个指标的线性组合

如有两个原始变量x1和x2，则一共可提取出两个主成分如下：

z1=b11x1+b21x2 

z2=b12x1+b22x2

比如上面这张图，两个自变量存在共线性，我们提取两个主成分

原则上如果有n个变量，则最多可以提取出n个主成分，但如果将它们全部提取出来就失去了该方法简化数据的实际意义。多数情况下提取出前2~3个主成分已包含了90%以上的信息，其他的可以忽略不计。

在进行主成分回归时，提取出的主成分能包含主要信息即可，不一定非要有准确的实际含义。

 

用途：

主成分评价：当进行多指标的综合评价时，应用主成分方法将多指标中的信息集中为若干个主成分，然后加权求和，得到综合评价指数。（比如高校的综合排名，收集了一系列与排名有关的自变量，之后提取两至三个主成分，加权求和给出排名）

主成分回归：通过对存在共线性的自变量进行主成分分析，从而在提取多数信息的同时解决共线性问题。

 

注意：由于各自变量测量尺度范围不一样，使用主成分/因子分析之前应做变量的标准化，但是SPSS自动做了

 

案例：各省经济发展情况综合评价

现希望根据全国30个省市自治区经济发展基本情况的八项指标对其进行分析和排序。具体指标有：GDP、居民消费水平、固定资产投资、职工平均工资、货物周转量、居民消费价格指数、商品零售价格指数、工业总产值。

数据集如下

1	北京	1394.89	2505.00	519.01	8144.00	373.90	117.30	112.60	843.43
2	天津	920.11	2720.00	345.46	6501.00	342.80	115.20	110.60	582.51
3	河北	2849.52	1258.00	704.87	4839.00	2033.30	115.20	115.80	1234.85
3	山西	1092.48	1250.00	290.90	4721.00	717.30	116.90	115.60	697.25
4	内蒙	832.88	1387.00	250.23	4134.00	781.70	117.50	116.80	419.39
5	辽宁	2793.37	2397.00	387.99	4911.00	1371.10	116.10	114.00	1840.55
6	吉林	1129.20	1872.00	320.45	4430.00	497.40	115.20	114.20	762.47
7	黑龙江	2014.53	2334.00	435.73	4145.00	824.80	116.10	114.30	1240.37
8	上海	2462.57	5343.00	996.48	9279.00	207.40	118.70	113.00	1642.95
9	江苏	5155.25	1926.00	1434.95	5943.00	1025.50	115.80	114.30	2026.64
10	浙江	3524.79	2249.00	1006.39	6619.00	754.40	116.60	113.50	916.59
12	安徽	2003.58	1254.00	474.00	4609.00	908.30	114.80	112.70	824.14
13	福建	2160.52	2320.00	553.97	5857.00	609.30	115.20	114.40	433.67
14	江西	1205.11	1182.00	282.84	4211.00	411.70	116.90	115.90	571.84
15	山东	5002.34	1527.00	1229.55	5145.00	1196.60	117.60	114.20	2207.69
16	河南	3002.74	1034.00	670.35	4344.00	1574.40	116.50	114.90	1367.92
17	湖北	2391.42	1527.00	571.68	4385.00	849.00	120.00	116.60	1220.72
18	湖南	2195.70	1408.00	422.61	4797.00	1011.80	119.00	115.50	843.83
19	广东	5381.72	2699.00	1639.83	8250.00	656.50	114.00	111.60	1396.35
20	广西	1606.15	1314.00	382.59	5105.00	556.00	118.40	116.40	554.97
21	海南	364.17	1814.00	198.35	5340.00	232.10	113.50	111.30	64.33
22	四川	3534.00	1261.00	822.54	4645.00	902.30	118.50	117.00	1431.81
23	贵州	630.07	942.00	150.84	4475.00	301.10	121.40	117.20	324.72
24	云南	1206.68	1261.00	334.00	5149.00	310.40	121.30	118.10	716.65
25	西藏	55.98	1110.00	17.87	7382.00	4.20	117.30	114.90	5.57
26	陕西	1000.03	1208.00	300.27	4396.00	500.90	119.00	117.00	600.98
27	甘肃	553.35	1007.00	114.81	5493.00	507.00	119.80	116.50	468.79
28	青海	165.31	1445.00	47.76	5753.00	61.60	118.00	116.30	105.80
29	宁夏	169.75	1355.00	61.98	5079.00	121.80	117.10	115.30	114.40
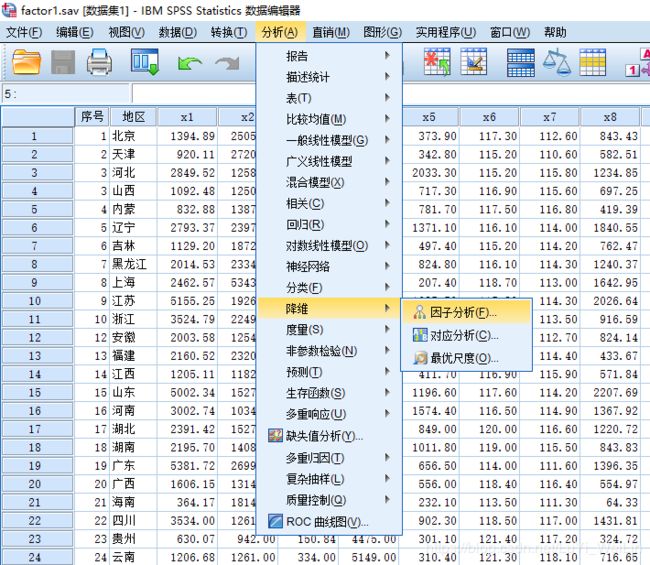
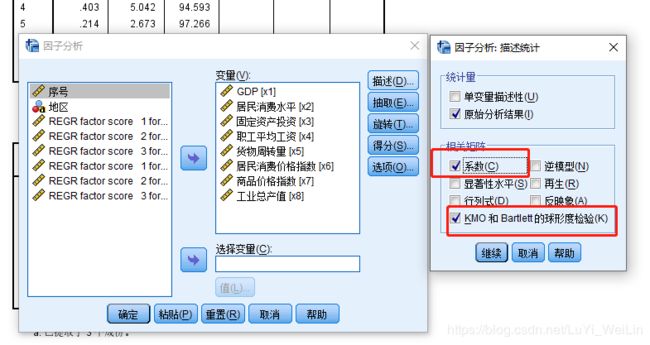
30	新疆	834.57	1469.00	376.95	5348.00	339.00	119.70	116.70	428.76

spss里面没有单独的主成分分析对话框，用分析--降维--因子分析来实现 

 

 把八个自变量加进来

 

 结果解读：

公因子方差：每个变量的信息量被提取的程度

信息：统计里所谓的信息实际上是变异的另外一种说法，统计数据里信息量的高低其实完全可以用离散程度大小或者标准差之间的大小加以反映

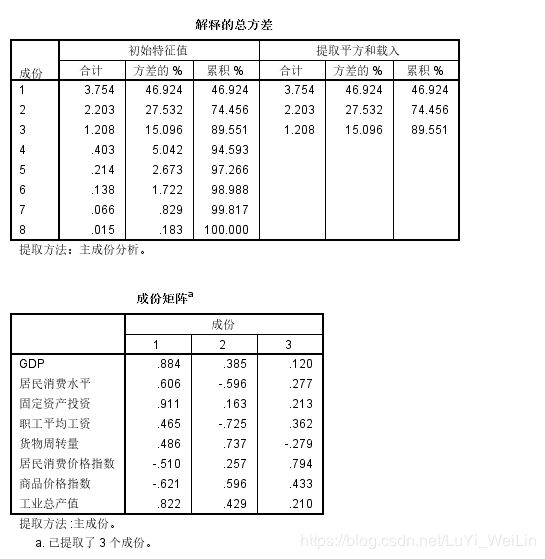
解释总方差：合计这一列代表提取出来的这个主成分携带的信息相当于多少个原始变量的信息；方差相当于对应提取出来的主成分携带了原始信息多少百分比，，看到结果只要了3个主成分，累计携带原始信息的89.551%

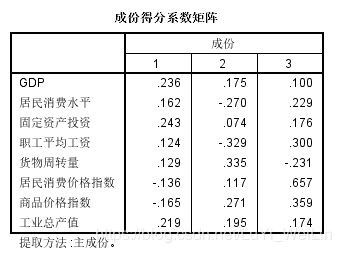
成份矩阵：（主成分与自变量之间的关联情况），要注意的是最左边的变量不是原始的自变量，而是经过标准化的变量，这里加完的主成分还要做一些变换才能和数据统计推出来的主成分一模一样，还要换算出常数项，但是这个步骤我们不需要自己手动计算，让SPSS自己计算每一个个案的相应主成分，好让我们后面进行分析（因子分析--得分--保存变量），每一个主成分的计算公式可以看成分得分系数矩阵（每一个主成分具体的计算公式），这个是成份矩阵经过换算得到的结果

SPSS自动计算每个变量的主成分出来，好让我们进行下一步的分析，之后可以用3个提取出来的主成分代替8个原始变量进行建模分析

 

因子分析

针对刚才的主成分分析，虽然可以解决变量之间的共线性，提取出主成分，但是我们也知道，有一些主成分可能不好解释，因子分析不光要提取信息，而且要求提取出来的共同因子能解释。

因子分析是一种多变量化简技术。目的是分解原始变量，从中归纳出潜在的“类别”，相关性较强的指标归为一类，不同类间变量的相关性较低。每一类变量代表了一个“共同因子”，即一种内在结构，因子分析就是要寻找该结构。

 

因子分析适用条件

因子分析相对于主成分分析来说会更加苛刻一点，主成分相对来说是没有条件限制的，而因子分析有条件限制：

• 样本量

样本量与变量数的比例应在5：1以上

总样本量不得少于100，而且原则上越大越好

• 各变量间必须有相关性

KMO统计量：0.9最佳，0.7尚可，0.6很差，0.5以下放弃（一般大于0.7做因子分析效果好，一般小于0.5不用考虑做因子分析）

Bartlett’s球形检验，一般小于0.05即可

 

因子分析的分类

• 探索性因子分析（这篇博客主要这个）

对内在结构不知，纯探索，不适用使用该方法下结论，要结合其他方法一起下结论才有说服性

• 证实性因子分析（结构方程模型加以解决这个问题）

之前已经探索足够了，已经大概猜得里面是什么结构了，用假设检验验证一下是否真的是这样的结构

 

举一个很简单的因子分析例子

比如在市场调查中收集了食品的五项指标：味道、价格、风味、是否快餐食品、能量。经过因子分析后发现结果如下：

x1=0.02z1+0.99z2+ε1

x2=0.94z1-0.01z2+ε2

x3=0.13z1+0.98z2+ε3

x4=0.84z1+0.42z2+ε4

x5=0.97z1-0.02z2+ε5

 

第一公因子主要影响价格、是否快餐食品和能量，代表“价廉”

第二公因子主要影响味道和风味，代表“味美”

ε代表特殊因子，只对当前变量有影响，表示该变量中独特的，不能被公因子所解释的特征

 

因子分析的用途

• 研究设计阶段/问卷效果评估阶段

评价问卷的结构效度（正常情况下，每一个问卷调查模块都会被提取成一个共同因子，每一个问卷调查模块都代表我们想研究的一个主题）

• 统计分析阶段

解决变量间多重共线性

寻找变量间潜在结构（探索性因子分析）

内在结构证实（证实性因子分析）

 

因子分析一般的分析步骤

• 判断是否需要进行因子分析，数据是否符合要求
• 进行分析，按一定标准确定提取的因子数目
• 如果进行的是主成分分析，则将主成分存为新变量用于继续分析，步骤到此结束
• 如果进行的是因子分析，则考察因子的可解释性，并在必要时进行因子旋转，以寻求最佳解释方式
• 如有必要，可计算出因子得分等中间指标供进一步分析使用

 

公因子数量的确定

• 主成分的累积贡献率：80~85%以上
• 特征根：大于1
• 综合判断
• 因子分析时更重要的是因子的可解释性（必要时可保留小于1的因子，碎石图可以帮助确定因子数量）

 

因子分析有关概念

• 因子负荷

即表达式中各因子的系数值，用于反映因子和各个变量间的密切程度，其实质是两者间的相关系数

• 公因子方差比（Communalities）

指的是提取公因子后，各变量中信息分别被提取出的比例，或者说原变量的信息量（方差）中由公因子决定的比例

• 特征根（Eigenvalue）

可以被看成是主成分影响力度的指标，代表引入该因子／主成分后可以解释平均多少原始变量的信息。

正因如此，一般对特征根大于1的因子才加以注意

 

另一个比较好的案例大家可以看http://cda.pinggu.org/view/25642.html

案例：对各省经济数据的进一步分析

我们接上一个主成分分析的例子,虽然样本量不满足因子分析适用条件，但是实际上地区不能再增加了，我们只能根据结果解释的时候谨慎一些

 

KMO<0.7,不太适用因子分析，但是KMO>0.6,可以尝试做一下，没小于0.5

球形检验<0.05证明自变量之间是存在关联关系的，并非全部都是独立的

刚才我们勾选了变量之间的系数相关矩阵，可以看变量之间的关联性

得到结果的解释的总方差和成分矩阵和之前的主成分分析结果一致，但是我们看到第一个因子和所有自变量几乎都有关系，不好解释，没找到其内在结构，没能找到其更加准确的方向，后面两个因子被第一个因子提取的信息量多了

 针对上面这个情况，如何让因子解释更加完美呢？

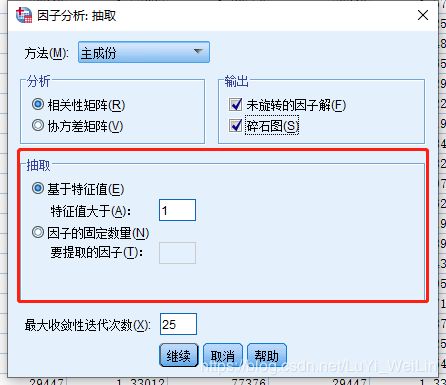
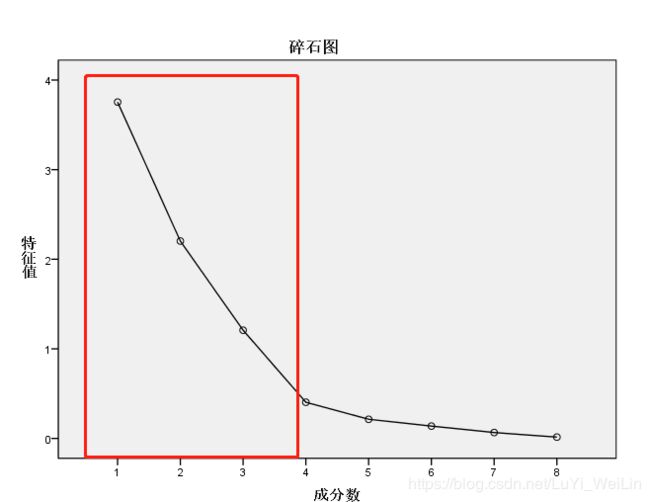
• 选定因子的个数，有一个帮我们辅助选变量的图--碎石图

如何设置因子的个数（可以基于特征根选择，也可以基于固定数量选择）

一

般陡坡才有价值，目前来说我们选择三个是没有错误的

• 使用公因子旋转，让解释更加完美

把提取出来的信息重新再分配，之前是第一个公因子尽可能提取多的信息量，第二个公因子提取第一个公因子剩余信息的尽可能多的信息，因子旋转让公因子之间差距尽量大，一个公因子代表一个方向，让其有一个合理的解释

旋转后的因子重新分配结果

具体如何分配（原始成分矩阵转换为新的旋转成分矩阵）

旋转后的公因子解释强了，看第一个因子从之前的和所有自变量有关变为之和GDP、固定资产规模、货物周转以及工业总产值有关，我们可以解释为GDP发展因子

旋转后的公因子的得分矩阵（看旋转后的公因子如何计算），比如

第一个因子=0.306*标准化的GDP+0.25*标准化的居民消费水平+。。。。。

对于结果不好观看，我们可以设置一下

系数是指公因子和变量的相关系数

取消小系数指的是，不显示相关性非常弱的系数，我们知道公因子和变量的相关性的平方就是决定系数，决定系数代表信息量可以被解释的比例，0.1携带信息量是0.01，我们可以设置0.3，携带小于9%的系数剔除掉，显示成这样就非常好解读

 

• 载荷图

载荷图把旋转之后的成分矩阵用图表显示出来，一般两个因子时候适合，多个的时候不好观察

 

 

因子分析补充：

• 加入旋转后的因子还是找不到其内在结构，我么可以换旋转方法，实在不行也不要逞强，那就真的找不到这个结构

 

• 可能我们默认使用因子分析旋转后的得到结果已经解释的很完美了，但是还是要结合碎石图考虑特征根小于1的变量，说不定得到的解释会更加完美