GNN金融应用之Classifying and Understanding Financial Data Using Graph Neural Network学习笔记

阅读该文献，记录中文翻译，方便复习。

摘要

从不同应用程序收集的实际数据通常不具有预定义的数据模型或未以预定义的方式组织。 难以分析凌乱的非结构化数据并提取有用的数据信息。对于在金融机构中收集的数据，通常具有附加的拓扑结构，并且可以用图形表示。 例如，社交网络，通信网络，金融系统和支付网络。可以从每个实体（例如金融机构，客户或计算中心）的连接中构建图结构。 我们通过基于图结构的标签预测问题，分析不同实体如何影响彼此的标签。有了结构化数据，GNNs就是一个功能强大的工具，可以模仿专家来标记节点。 GNN通过图结构组合节点特征，使用神经网络嵌入节点信息并将其通过图的边传递。我们想要通过识别GNN模型的输入数据中的信息交互来实现图中节点的分类，并检查模型是否按我们的期望工作。 然而，由于复杂的数据表示和非线性转换，解释GNN做出的决策具有挑战性。在这项工作中，我们提出了用于金融交易数据的图表示方法和新的图特征的解释方法，以识别信息丰富的图形拓扑。 我们使用四个数据集（一个合成的和三个实数）来验证我们的方法。 我们的研究结果表明，图结构表示法有助于分析金融交易数据，而我们的解释方法可以模仿人类解释的模式并解决图中的不同特征。

1. 概述

近年来，随着大数据，云计算，人工智能等新技术的迅猛发展，这些新技术已与金融服务深度融合，释放了金融创新的生命力和应用潜力，极大地促进了金融业的发展。在这一发展过程中，大数据技术是最成熟，应用最广泛的技术。但是，面对如此广阔的信息，尤其是非结构化数据信息，如何存储，查询，分析，挖掘和利用这些庞大的信息资源尤为关键。传统的关系数据库主要面向交易过程和数据分析应用程序。他们擅长解决结构化数据管理问题。管理非结构化数据存在一些固有的缺陷，尤其是在处理大量非结构化信息时。为了应对非结构化数据分析的挑战，一种策略是将非结构化数据转换为结构化数据，这将有助于类似的信息标记，检索，查找和聚类，并将有助于更好地为实体经济服务并有效促进金融业的整体发展。
我们的当代社会高度依赖人际关系/文化关系（社会网络），我们的经济紧密联系和结构化（商业关系，金融转移，供应/分配链），地缘政治关系也非常结构化（商业和政治联盟），它还依赖于运输网络（公路，铁路，海上和航班连接），而且我们的网络系统在结构上也相互连接（计算机网络，互联网）。而且，那些复杂的网络结构也出现在自然界中，出现在诸如大脑，血管和神经系统的生物系统，也出现在化学系统，例如分子的原子连接。如今，利用现代技术，我们从上述所有系统及其关系中收集数据，因为该数据极度结构化且严重依赖于网络内部的关系，因此将数据表示为图是有意义的，其中节点表示实体和边表示他们之间的联系。
人工智能正在成为金融大数据应用的新方向。诸如GCN（Kipf和Welling 2016），GraphSage（Hamilton，Ying和Leskovec 2017）之类的图神经网络（GNN）是一种深度学习架构，可以通过保留图的信息结构来处理图结构数据。我们着重于节点标记问题，例如欺诈检测，信用发放，客户定位，社交网络用户分类，它们可以模仿专家对节点标记的决定。GNN通过使用神经网络嵌入节点信息并将其通过图的边传递，从而能够组合节点特征，连接模式和图形结构。然而，由于复杂的数据表示和对数据执行的非线性转换，解释GNN做出的决策是一个具有挑战性的问题。图1是一个关于从解释GNN节点分类决策来理解诈骗检测的例子。

尽管在卷积神经网络（CNN）中已经开发了深度学习模型可视化技术，但这些方法并不直接适用于解释用于进行分类任务的具有节点特征的加权图。关于解释GNN的工作很少（（Pope等人2019; Baldassarre和Azizpour 2019; Ying等人2019; Yang等人2019））。但是，据我们所知，还没有已完成的关于解释加权图中的综合特征（即节点特征，边特征和连接模式）的工作，特别是对于节点分类问题。在这里，我们提出了几种基于图形结构的图形特征解释方法来表示财务数据。我们使用三个数据集（一个合成数据和两个真实数据）来验证我们的方法。我们的结果表明，通过使用解释方法，我们可以发现用于节点分类的数据模式与人工解释相符，并且这些解释方法可以用于理解数据，调试GNN模型和检查模型决策以及其他任务。
我们的工作总结如下：
1. 我们提出将金融交易数据转移到加权图表示中，以进行进一步分析和理解数据信息。
2. 我们建议使用GNN分析金融交易数据，包括欺诈检测和帐户匹配。
3. 我们提供解释结构化图形中的实体标记时实体之间的信息交互。
论文结构：在第2节中，我们介绍图表示。然后在第3节中，我们将逐步介绍GNN中的操作。在第4节中，描述了图形解释的公式，并介绍了相应的方法。在第5节中，我们提出了评估指标和方法。实验和结果在第6节中介绍。我们在第7节中总结本文。

2. 数据表示-加权图

对于包含用户和交互信息的财务数据，我们可以将每个实体建模为一个节点，并基于它们之间的交互在它们之间建立连接。在本节中，我们介绍必要的符号和定义。我们用$G=(V,E)$表示一个图，其中$V$是节点集，$E$是链接节点的边集，$X$是节点特征集。对于每对相连的节点$u,v\in V$，我们用$e_{vu}\in R$表示连接它们的边$(v,u)\in E$的权重。我们表示$E[v,u]=e_{vu}$，其中$E\in R^{|E|}$。对于每个节点$u$，我们关联特征的d维向量$X_u\in R^d$，并将所有特征的集合表示为$X=\left\{X_u:u\in V\right\}\in (R^d{)}^{|V|}$。
边特征包含有关图形的重要信息。例如，图$G$可以表示一个银行系统，其中节点$V$代表不同的银行，而边$E$是它们之间的交易；图$G$也可以代表一个社交网络，其中节点$V$代表不同的用户，边$E$是用户之间的接触频率。我们考虑节点分类任务，其中为每个节点$u$分配标签$y_u\in I_C=\left\{0,...,C-1\right\}$。在金融应用程序中，节点分类问题可能是欺诈检测，新客户发现，帐户匹配等。

3. GNN利用边权值

与现有的GNN架构不同，即图卷积网络(GCN)(Kipf和Welling 2016)和图注意力网络(GAT)(Velickovic等2018)，某些GNN可以利用图上的边信息(Gong 和Cheng 2019; Shang et al.2018; Yang et al.2019)。在这里，我们考虑加权有向图，并建立使用节点和边权重的图神经网络，其中边权重会影响消息聚合。我们的方法不仅可以处理有向加权图，而且可以在GNN的传播中保留边信息。对于许多现实场景，例如银行支付网络，推荐系统（使用社交网络）以及其他严重依赖于连接拓扑的系统，保留和使用边信息非常重要。这是因为除了节点（原子）特征之外，边（键）的属性对于预测图形的局部和全局属性也很重要。一般而言，GNN通过递归聚合和转换其相邻节点的特征向量来归纳学习节点表示。参考(Battaglia等人2018; Zhang,Cui和Zhu 2018; Zhou等人2018)，在我们的集合中GNN的每层更新涉及这三个计算，即消息传递等式(1)，消息聚合等式(2)，并更新节点表示式(3)，可以表示为：
$$m_{vu}^{(l)}=MSG(h_u^{(l-1)},h_v^{(l-1)},e_{vu})\text{\hspace{1em}(1)}$$
$$M_i^{(l)}=AGG(\left\{m_{vu}^{(l)},e_{vu}\right\}|v\in N(u))\text{\hspace{1em}(2)}$$
$$h_u^{(l)}=UPDATE(M_u^{(l)},h_u^{(l-1)})\text{\hspace{1em}(3)}$$
其中$h_u^{(l)}$是l层上节点u的嵌入式表示；$e_{vu}$是从v指向u的加权边；$N(u)$是u的邻居，在此收集信息以更新其汇总消息$M_i$。具体来说，$h_u^{(0)}=x_u$作为初始值，$h_u^{(l)}$是GNN节点分类器的L层节点u的最终嵌入。
参考(Schlichtkrull等人2018)，可以使用以下步骤形成使用边权重进行滤波的GNN层：

其中N(u)表示节点u的邻居集合，e_vu表示从v到u的有向边，W表示要学习的模型参数，并且φ是可应用于邻居节点特征的任何线性/非线性函数 嵌入。我们设置h^(l) ∈R^d(l)，而d^(l)是第l层表示的维度。
正如（Gong and Cheng 2019）中的图卷积运算，边特征矩阵将用作过滤器乘以节点特征矩阵。为了避免相乘使得输出特征的规模增大，需要对边特征进行归一化，如GAT（Velickovic等2018）和GCN（Kipf和Welling 2016）一样。由于存在聚集机制，我们将权重通过入度${\bar{e}}_{vu}=e_{vu}/{\sum }_{v\in N(u)}{e}_{vu}$进行归一化。我们的方法可以通过将负边权重重归一化为正间隔来处理，例如[0,1]，因此在下面，我们仅使用正加权边，并且将边权重用作消息过滤。根据问题：

• g可以简单定义为： $g={\bar{e}}_{vu}{m}_{vu}^{(l)}$
• g也可以是门函数，例如rnn类型的模块 $m_{vu}^{(l)}$，即 $g=GRU({\bar{e}}_{vu}{m}_{vu}^{(l)},h_u^{(l-1)})$

4. 解释图结构数据的信息成分

图中的关系结构通常包含用于节点分类的重要信息，例如图的拓扑和信息流（即方向和幅度）。因此，了解哪些边对进出节点的信息流贡献最大，对于理解和解释节点分类至关重要。
我们将加权图形特征解释问题作为two-stage的管道来解决。首先，我们训练GNN节点分类函数。GNN输入是一个图形$G=(V,E)$，其关联节点的特征为X和其真实的节点标签为Y。我们将该分类器表示为$\Phi ：G\mapsto (u\mapsto y_u)$，其中$y_u\in I_C$。GNN的优点之一是保留了跨节点的信息流以及数据结构。此外，它对于顺序的排列是不变的。因此，它保持了输入数据的相关归纳偏差（请参阅（Battaglia et al.2018））。其次，给定节点分类模型和节点的真实标签，解释部分提供了一个子图和一个从每个节点u的k-hop邻域检索的特征子集，$k\in N$和$u\in V$。子图以及特征子集是GNN用于计算节点标签的信息和跨u邻居节点的信息流的最小集合。我们将$G_S=(V_S,E_S)$定义为G的子图，其中如果$V_S\subseteq V$和$E_S\subseteq E，G_S\subseteq G$。考虑节点u的分类$y_u\in I_C$，则信息组件检测将计算子图$G_S$，包含u，旨在通过查看边连接模式$E_S$及其连接节点$V_S$来解释分类任务。这种方法提供了有助于对节点进行标记的图形特征。

4.1 最大互信息 (MMI) Mask

由于GNN的特性，(5)，我们只需要考虑聚合中使用的图结构，即关于节点u的 计算图定义为$G_c(u)$，包含$N^{\prime }$个节点，其中$N^{\prime }\le N$。与$G_c(u)$关联的节点特征集为$G_c(u)=\left\{x_v|v\in V_c(u)\right\}$。对于节点u，GNNΦ的标签预测由$y_u$ =$\Phi (G_c(u),X_c(u)$)给出，这可以解释为GNN映射的分布$P_{\Phi }(Y|G_c,X_c)$。我们的目标是确定子图$G_S$ ⊆ $G_c(u)$（及其关联特征$X_S=\left\{x_w|w\in V_S\right\}$或它们的子集），GNN用以预测u的标签。
利用信息论（Cover和Thomas 2012）以及GNNExplainer（Ying等人，2019）的思想，选择信息丰富的可解释子图和节点特征子集以最大化互信息（MI）：

由于训练后的GNN节点分类器$\Phi$是固定的，因此公式(7)的H(Y)项是恒定的。因此，等效于将条件熵$H(Y|G_S,X_S)$最小化：
$$-{\mathbb{E}}_{Y|G_S,X_S}[log{P}_{\Phi }(Y|G_S,X_S)]\text{\hspace{1em}(8)}$$
因此，对与节点u的预测${\hat{y}}_u$相关的具有预测能力的图分量的解释是子图$G_S$及其相关特征集$X_S$使得式(8)最小。因此，解释的目的是选择信息量最大的边及其连接的邻域，它们构成一个子图，以预测u的标签。因为，u的计算图$G_c(u)$中的某些边可能会形成重要的消息传递(5)路径，这些路径允许有用的节点信息在$G_c(u)$上传播并在u处聚集以进行预测；而$G_c(u)$中的某些边可能无法提供预测信息。代替直接优化(8)中的$G_S$，因为存在包含$N^{\prime }$个节点的指数级离散结构$G_S$ ⊆ $G_c(u)$，所以GNNExplainer（Ying等人，2019年）在二进制相邻矩阵上优化了mask $M_{sym}^{N^{\prime }\times N^{\prime }}[0,1]$ ，允许在$G_S$上执行梯度下降。
如果我们使用边权重进行节点嵌入，则可以将连接视为二进制并适合原始GNNExplainer。但是，如果我们将边权重用作过滤，则mask应影响过滤和规范化。我们通过考虑边权重来扩展原始的GNNExplainer方法，并通过添加额外的正则化来改进该方法。与GNNExplainer不同，我们没有限制mask值，而是对由mask学到的值进行了限制，并且采用梯度下降法进行了优化。
$$\sum _w{\mathrm{M}}_{vw}{e}_{vw}=1,{\mathrm{M}}_{vw}⩾0,for(v,w)\in {ϵ}_c(u)\text{\hspace{1em}(9)}$$
因此，假设在$G_c(u)$中存在Q个边，不同于在GNNExplainer中优化松弛邻接矩阵，我们对加权边上的mask $M\in [0,1{]}^Q$进行了优化。然后$E_c^M=E_c\odot M$，其中$\odot$是两个矩阵的逐元素乘法。被mask的边$E_c^M$受$E_c^M[v,w]\le Ec[v,w]，\forall (v,w)\in Ec(u)$ 的约束，则目标函数可写为：

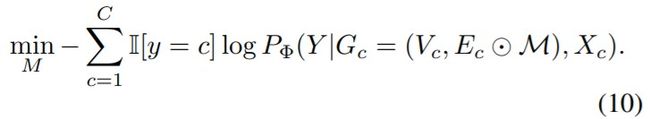
在GNNExplainer中，前k个边可能未形成包括预测$i$下的节点（例如$u$）在内的连接分量。因此，我们将指向节点$u^{\prime }$的每个节点v的$(E_c\odot M{)}_{vu}$熵添加为正则项，以确保选择至少一个连接到节点u的边。学习了mask $M$之后，我们使用阈值删除较小的$(E_c\odot M)$和孤立的节点。我们提出的优化方法是在上述约束下,优化M最大化互信息（等式(7)），如算法1所示。

4.2 Guided Gradient (GGD) Salience

基于梯度的指导性解释方法（Simonyan，Vedaldi和Zisserman 2013）也许是最直接，最简单的方法。通过简单地计算不同输入相应的输出差异，然后应用范数，可以获得得分。基于梯度的得分可用于指示输入特征的相对重要性，因为它表示输入空间中的变化，该变化对应于模型输出中最大的正变化率。由于边权重已在GNN中用作过滤器，我们可以获得边mask为

其中c∈{1, … , C}是节点u的正确类别，而$y_u^u$是softmax层之前的类别c的得分。其中$x_v$是节点v的特征。在这里，我们在前k个边中选择$g^E$最大的边及其连接节点。对比梯度显着性方法的优点是易于计算。但是，有人认为它的性能通常比新技术差（Zhang等人2018; Selvaraju等人2017）。

4.3 Edge Weighted Graph Attention (E-GAT)

图注意力层采用一组节点特征$H^{(l-1)}=\left\{h_1^{(l-1)},h_2^{(l-1)},\cdot \cdot \cdot ,h_N^{(l-1)}\right\}，x_i\in {\mathbb{R}}^F$ 作为输入，并将它们映射到$H^{(l)}=\left\{h_1^{(l)},h_2^{(l)},\cdot \cdot \cdot ,h_N^{(l)}\right\}，h_i^{(l)}\in {\mathbb{R}}^{d^{(l)}}$ 。遵循自注意机制Att：${\mathbb{R}}^{d^{(l)}}\times {\mathbb{R}}^{d^{(l)}}⟶\mathbb{R}$（Velickovi和其他人，2018年）,聚集1-hop邻域节点$\left\{h_v^{(l-1)},\forall v\in N(u)\right\}$来计算每个节点v∈V的嵌入式表示。与原始版本（Velickovi和其他人，2018年）不同，我们利用了underlying图的边权重。修正注意力${\alpha }_{vu}\in \mathbb{R}$可以表示为$x_v$和$x_w$的单个前馈层，边权重为$e_{v}u$：

其中α是v→u的注意力权重，它表示节点j的特征对节点i的重要性。它允许每个节点根据其节点功能（通过underlying连接性加权）参加图上的所有其他节点。$W_a\in {\mathbb{R}}^{d^{(l)}}\times {\mathbb{R}}^{d^{(l)}}$是可学习的线性变换，它将每个节点的特征向量从维$d^{(l-1)}$映射到嵌入维$d^{(l)}$。注意机制Att由节点属性学习向量$a\in {\mathbb{R}}^{2d^{(l)}}$和输入斜率0.2的LeakyRelu实现。为了explanation，我们对源节点之间的权重进行了归一化以使系数在不同边之间具有可比性：

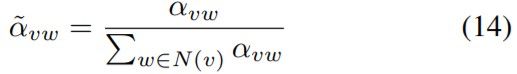
其中T(v)是v指向的目标节点集。然后，在图卷积层之前将有一个注意力嵌入层：

然后，我们对各层得到的注意力取均值。

4.4 Culturing Node Class Sensitivity

对于每个节点u，我们计算将其标记为类i ∈ {0, …, C − 1}的敏感度，与计算图$v,w\in V_c(u)$\u的所有节点相关

然后，我们对前一个矩阵的每个行向量进行聚类，以获得具有相同贡献模式的邻居节点集，以将节点u分类为i∈$I_C$。
此方法可用于验证信息子图上的节点是否具有相同的节点特征敏感性。同样，它可以显示$G_c$中邻居之间的相似性。

5. Evaluation Metrics and Methods

对于合成数据，我们可以将解释与数据生成规则进行比较。但是，对于真实数据，我们没有解释的依据。为了评估结果，我们提出了用于量化解释结果的评估指标，并提出了相关方法来验证边连接模式或节点特征是否是分类的关键因素。我们定义度量的一致性，对比性和稀疏性（此处，对比性和稀疏性的定义与（Pope等人2019）中的定义不同）以测量信息量丰富的成分检测结果。首先，为了测量图之间的相似性，我们引入图编辑距离（GED）（AbuAisheh等人，2015年），类似于字符串的Levenshtein距离的图相似性度量。它定义为将图G1转换为同构图到G2的最小编辑路径消耗（节点和边编辑操作的序列）。在结构同构但边权重不同的情况下。如果GED = 0，则在GED上添加Jensen-Shannon发散（JSD）（Nielsen 2010），以进一步比较两个同构子图。具体来说，我们将一致性定义为同一类节点的信息子图之间的GED，这是因为同一类节点的信息成分相一致；我们将差异性定义为不同类别的节点的信息子图之间GED，这是因为不同类别的节点检测到的信息成分是否具有差异性；稀疏度被定义为mask ${\sum }_{e_{vw}\in G_C(u)}{{\rm Y}}_{vw}/Q,{\rm Y}\in \left\{M,g^E\right\}$的密度，即分量边重要性权重的密度。

6. Experiments

请注意，下面所有图的颜色代码都遵循图2中的标记。红色节点是我们尝试分类和解释的节点。

6.1 Synthetic Data

数据 参考（Ying等人，2019），我们生成了一个带有15个节点的Barabasi–Albert（BA）图，并在随机节点上附加了10个5-node房屋结构图，在图2中以65个节点结束。为了便于可视化，我们制作了小图。但是，实验结果适用于大型图。可以认为包括互联网、引文网络、社交网络和银行支付系统在内的几种自然和人为系统近似于BA图，该图肯定包含极少数高度异常的节点（集线器）和大量节点连接不良。与不同节点对相连的边也被分配了不同的权重，如图2所示，其中w是边权重，我们将在后面讨论。然后，我们通过均匀随机地添加0.1N条边，将噪声添加到合成数据中，其中N是图中的节点数。为了约束节点标签仅由图案确定，所有节点特征$x_i$被设计为具有相同常数的二维节点属性。

GNN训练 我们使用等式(4)中的$g={\bar{e}}_{vu}{m}_{vu}^{(l)}$。参数设置为$input$_$dim=2，hidden$_$dim=8，num$_$layers=3$和$epoch=300$。我们随机分配60％的节点进行训练，其余部分用于测试。


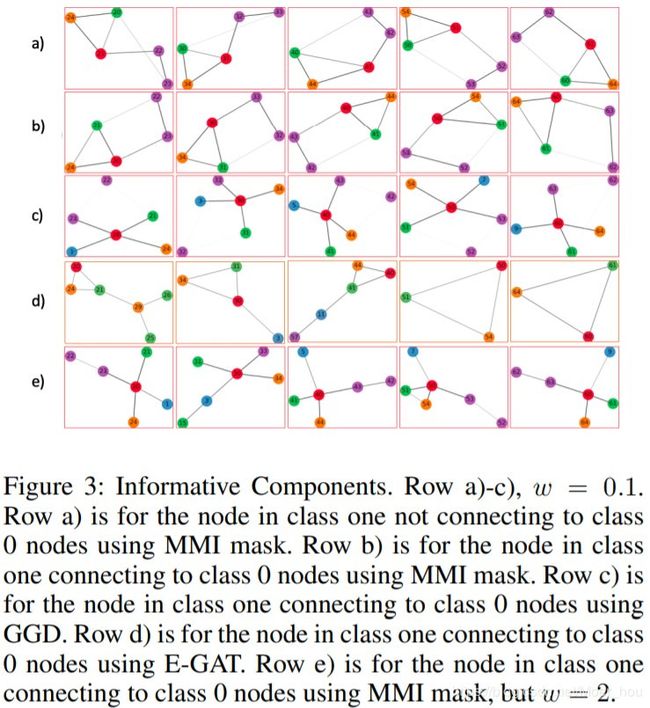
结果 GNN在训练和测试数据集上分别达到了100％和96.7％的准确性。 我们进行了信息组件检测（保留了前6个边），并将其与人工解释的“房屋形状”进行了比较，可以将其用作真实性检查（表1）。在图3中，我们显示了在相同位置但具有不同拓扑结构（行a和b）的节点的解释结果，并比较了八个权重对结果的影响（行a＆e）。我们还显示了通过不同方法（行a＆c＆d）生成的结果。

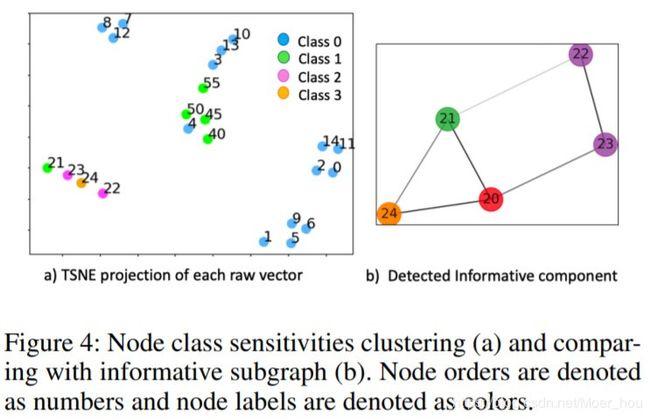
我们在图4中显示了SynComp上20个节点的聚类结果。节点21-24被聚在一起（在图4(a)中由T-SNE在二维空间中可视化(Maaten和Hinton 2008)），因为它们对于预测节点20为类别1最敏感，这与文中图（4(b)）显示的信息成分相匹配。其他簇通过对{0, 2, 3}中的某个类敏感的显着性对Gc(u)中的节点进行分组。
此方法可用于验证信息子图上的节点是否具有相同的节点特征敏感性。同样，它可以显示$G_c$中邻居之间的相似性。

6.2 Bitcoin OTC Data

比特币是一种用于匿名交易的加密货币。由于匿名，存在交易对手风险。我们使用一个月内收集的比特币数据集(Kumar et al.2018)，其中比特币用户对与其进行交易的用户的信任程度进行评估。等级范围从-10到+10（0除外）。 根据OTC的指南，评分越高，就越值得信赖。我们将评分列表中有一个负分的用户标记为有风险；超过一半获得评分大于1的用户是值得信赖的用户；没有收到评分的用户为未知组；其余的用户则分配到了中性组。我们选择一个时间点的评分网络数据，其中包含1447个用户，5739个评分记录。我们通过${\tilde{e}}_{ij}=e_{ij}/20+1/2$将边权重重新归一化为[0,1]。然后，我们在包含90％未知，中性和可信赖的节点，20％风险节点（仅这些节点）的数据集上训练了GNN，并对其余节点执行分类。我们选择g为GRU门，其他设置是$hidden$_$dim=32，num$_$layers=3$和$epoch=1000$。学习率初始化为0.1，并且每100个epoch减少一半。我们在训练数据集上的准确性为0.730，在测试数据集上的准确性为0.632。最后，我们使用MMI mask显示了解释结果，因为它更易于解释（参见图5），并将它们与可能的人类推理进行了比较。风险节点的信息组分的模式包含负评分；对可信任节点的主要评分大于1；对于中性节点，它获得了很多的评分1。信息量与我们标记节点的规则匹配。

6.3 Bank Transaction Data - Account Matching

我们使用包含1000个国际支付交易记录的数据库，其中涉及四方，即始发（ORG）帐户，发送（SND）银行，接收（RCV）银行和受益人（BEN）帐户。各方均参与交易，可能的集合为$I_4$ = {ORG, SND, RCV, BEN}。任务是将每个节点分类为帐户（ORG或BEN）或银行（SNF或RCV），因为输入图数据有噪声。为此，我们使用支付数据构建交易图，节点是银行帐户；节点之间的交易是图中的有向边；交易金额是边特征。 此外，每个节点都与分类特征（“用户ID类型”和“国家”）相关联。我们使用one hot编码将节点特征转换为10×1向量，并将边特征归一化为[0,1]。我们标记了10％的数据，并训练了GNN将每个帐户分类为银行帐户和客户帐户。我们使用与合成数据实验中所述相同的GNN架构，并使用固定学习率0.01的Adam优化方法训练模型100epoches，直到收敛为止。节点分类任务的准确性为100％。使用我们的解释算法，我们呈现出每种帐户类型（客户帐户或银行帐户）中检测到的信息组分的可视化，如图6所示。
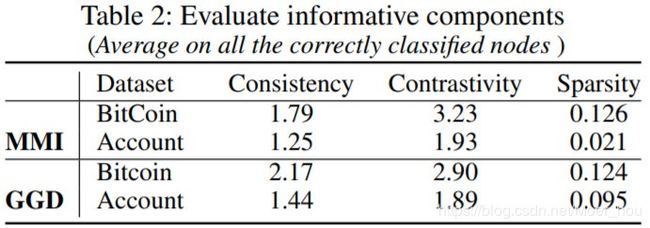
对于上述两个真实数据集，我们通过选择顶部的4条边来测量一致性，对比度和稀疏性。由于当在GNN中添加关注层时，我们无法在真实数据集中获得良好的分类结果，因此我们仅将MMI掩码和GGD方法应用于真实数据中的信息成分检测。表2列出了MMI掩码和GGD方法的度量。与一致性值相比，较高的对比度值表明GNN在数据拓扑信息上针对节点分类有效，并且同一类别中的节点具有相似的拓扑结构。低稀疏值表示信息成分具有较高的信息熵，说明了从财务数据中提取信息模式的解释方法的潜力。

7. Conclusion

在这项工作中，我们将财务系统中的交易数据公式化为加权有向图。我们在GNN节点分类任务中对加权图应用解释方法，可以对GNN中使用的数据交互模式提供主观和全面的解释。我们还提出了评估指标和方法来验证解释结果。这些解释可能有益于调试，特征管理，通知人类决策，建立信任等。我们的未来工作将包括将解释扩展到具有多维边特征的图，并解释不同的图学习任务，例如链接预测和图分类。