堆排序及其优化过程总结
引言:众所周知,堆排序算法是高级排序算法中的一种,平均时间复杂度为O(nlogn),算法思想是:先把带排序的记录构造成堆,然后通过从堆中不断选取最小/大元素,从而达到排序的目的。本文将以最大堆为例从三个点依次讨论堆排序的优化,即从基础堆排序到heapify、再到原地堆排序讨论。以下共有三个堆排序算法(heapSort1、heapSort2、heapSort3)依次由浅入深讨论。(动图源于网络)
![]()
1.基础堆排序
以下先创建一个堆,然后通过put操作依次把数组中的元素插入到堆里,其中每次put操作都会动态地把堆中的元素按照堆序性排好序。输出的时候,如果是从升序,则倒序把堆中最大的元素放到数组中。
public static void heapSort1(int[] a,int n){
MaxHeap heap = new MaxHeap(100);
for(int i=0;ifor(int i=a.length-1;i>=0;i--)
a[i] = heap.removeMax();
} 其中,堆的数据结构如下:
class MaxHeap{
private int n; //堆的可容量大小
private int count; //索引
private int[] data; //创建堆时需要的额外空间,此处以int为例,也可以是其他类型
public MaxHeap(int n){//设堆根元素下标从1开始
data = new int[n+1];
this.count = 0; //初始堆中元素为空
this.n = n;
}
public void put(int x){ //插入一个堆元素
if(count+1>n) System.exit(0); //数组越界则退出程序
data[++count] = x;
shiftUp(count);
}
public int removeMax(){
if(count<1) System.exit(0); //数组越界则退出程序
int x = data[1];
Swap(data,1,count--);
shiftDown(1);
return x;
}
private void shiftUp(int k){
while(k>1&&data[k/2]2);
k /= 2;
}
}
private void shiftDown(int k){
while(2*k<=count){ //左孩子是否存在
int i = 2*k;
if((i+1<=count)&&(data[i]1])) //左右孩子
i++;
if(data[i]<=data[k]) break;
Swap(data,i,k);
k=i;
}
}
public int size(){ //堆元素个数
return count;
}
public boolean isEmpty(){ //判空
return count==0;
}
} 以上在put()和removeMax()方法中最关键的是shiftUp和shiftDown操作。当需要向堆中插入一个元素时(尾部插入),很可能破坏了原始的堆的堆序性。这时候就需要通过shiftUp操作使新插入的元素和其父节点依次比较大小,并在合适条件下交换元素位置,这是一种上升的操作。
private void shiftUp(int k){
while(k>1&&data[k/2]2);
k /= 2;
}
} 而当从堆中移除根元素时,此时把堆的尾部元素移到根元素位置,也一定破坏了堆序性。此时需要通过shiftDown操作和其左右子树做比较,并适当交换位置,这是一种下降的操作。
private void shiftDown(int k){
while(2*k<=count){ //左孩子是否存在
int i = 2*k;
if((i+1<=count)&&(data[i]1])) //左右孩子
i++;
if(data[i]<=data[k]) break;
Swap(data,i,k);
k=i;
}
} 运行结果如下:
初始数组:49 38 65 97 76 13 27
排序数组:13 27 38 49 65 76 97 以上由此不难发现一个问题,就是排序的时候需要依次将待排序数组元素插入,每插入一次执行一次shiftUp操作动态维护堆序性。那可不可以在乱序的数组中直接把它变化成具有堆序性的数组呢?答案是肯定的,由此诞生了第二个算法,此过程被称为“Heapify”。
2.Heapify
以下没有了一个一个将待排序元素插入堆的操作,而是通过构造方法在创建堆的同时传入待排序数组,此时堆中的元素已经满足堆序性。出堆的操作和前面相同。
public static void heapSort2(int[] a,int n){ //heapify
MaxHeap heap = new MaxHeap(a,a.length);
for(int i=a.length-1;i>=0;i--)
a[i] = heap.removeMax();
}其原理是先把传进来的数组原封不动复制到data[]数组中,然后从堆中最后一个非叶结点至根节点开始,对扫描的每一个元素执行shiftDown操作。
如图所示:
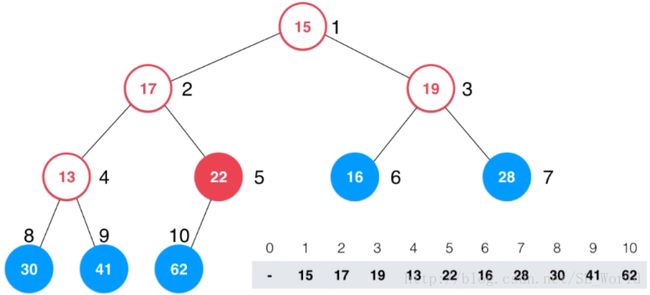
上图中最后一个非叶结点是索引为5的元素,从此结点开始遍历至根结点,每个结点执行一次shiftDown操作,遍历完成后此数组即为满足堆序性的数组。
优化的构造方法代码如下:
public MaxHeap(int[] a,int n){
data = new int[n+1];
this.count = n;
this.n = n;
for(int i=0;i1] = a[i];
for(int i=count/2;i>=1;i--)
shiftDown(i);
} 附优化后完整的堆的数据结构:
class MaxHeap{
private int n; //堆的可容量大小
private int count; //索引
private int[] data; //创建堆时需要的额外空间,此处以int为例,也可以是其他类型
public MaxHeap(int[] a,int n){ //设堆根元素下标从1开始
data = new int[n+1];
this.count = n;
this.n = n;
for(int i=0;i1] = a[i];
for(int i=count/2;i>=1;i--)
shiftDown(i);
}
public int removeMax(){
if(count<1) System.exit(0); //数组越界则退出程序
int x = data[1];
Swap(data,1,count--);
shiftDown(1);
return x;
}
private void shiftDown(int k){
while(2*k<=count){ //左孩子是否存在
int i = 2*k;
if((i+1<=count)&&(data[i]1])) //左右孩子
i++;
if(data[i]<=data[k]) break;
Swap(data,i,k);
k=i;
}
}
public int size(){ //堆元素个数
return count;
}
public boolean isEmpty(){ //判空
return count==0;
}
} 小结:
①将n个元素插入到一个空堆中,时间复杂度是O(nlogn)。
②heapify过程中,时间复杂度为O(n)。
故在heapify过程中,降低了一定的时间复杂度。但深入到程序中,我们又会发现,在待排序数组传入构造器中时,还是先把其完整的复制到数组data[]中,heapify的过程是在data[]数组中完成的,消耗了额外的O(n)辅助空间。那可不可以直接在原始的待排序的数组上直接排序呢?答案也是肯定的,由此诞生了原地堆排序。
3.原地堆排序
原地堆排序算法思想是:只需要把当然数组中最大的元素和数组中最后一个堆元素依次交换位置,每交换一次位置,堆的元素个数就减少一个,同时也需要动态维护此时剩下堆中元素的堆序性。这样交换完毕后此数组便由一个待排序数组变为了升序数组(降序的话颠倒一下顺序即可)。如图所示:

代码中,①先将输入进来的待排序数组进行heapify操作,即从最后一个非叶结点到根节点遍历执行shiftDown操作,使其变成具有堆序性的数组,②然后再依次将根元素(最大的元素)与数组中最后一个堆元素交换位置,并对剩下的堆中元素执行shiftDown操作。具体实现如下:
public static void heapSort3(int[] a,int n){
//heapify过程
for(int i=(n-1)/2;i>=0;i--)
shiftDown(a,n,i);
for(int i=n-1;i>0;i--){
Swap(a,0,i);
shiftDown(a,i,0);
}
}修改后的shiftDown方法如下:
public static void shiftDown(int[] a,int n,int k){//索引从0开始,n表示堆中元素个数,k表示当前元素下标
while(2*k+1int i = 2*k+1;
if(i+11])
i++;
if(a[i]<=a[k]) break;
Swap(a,i,k);
k = i;
}
} 总结:由此可看出,原地堆排序既无需过多额外辅助空间,也不需要对额外空间的操作排序性能较前者更优。其额外辅助空间仅为交换元素时申请的空元素,故额外空间消耗为O(1)。另,堆排序是不稳定排序。