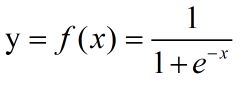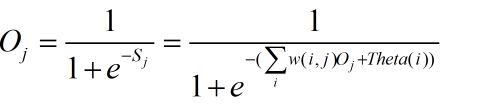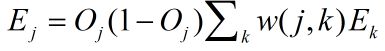神经网络的基础知识与简单分类编程
在我的下载里面有一些关于神经网络、遗传算法、粒子群优化算法等C语言基础编程。其实这些是两三年前上课写的了,当时一直没有做笔记的习惯,所以今天回过头来看很多自己都忘记了,所以准备现在将这些知识拾起来,写一个【智能信息处理】的专区,来回忆这些智能信息处理的算法。
我要写的第一篇就是《神经网络的基础知识与编程》
一、神经网络基础知识
人工神经网络(Artificial Neural Network,ANN)是科学家们在对生物的神经元、神经系统等生理学的研究取得突破性进展以及对人脑的结构、组成和基本工作单元有了进一步认识的基础上,通过借助数学和物理学方法从信息处理的角度对人脑神经网络进行抽象后建立的简化模型。
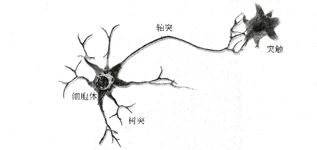
生物学对神经系统结构的研究成果是人工神经网络的基础。在生物界中,神经系统的基本单元是神经元。大多数神经元由一个细胞体和突两部分组成,神经元如下图1所示。突又分为两类,一是轴突,二是树突。轴突和树突共同作用,实现了神经元之间的信息传递。轴突的末端与树突进行信号传递的界面叫做突触,通过突触向其他神经元发送信息。对某些突触的刺激促使神经元触发。只有神经元所有输入的总效应达到阈值电平,它才开始工作。
图1 神经元结构
人工神经网络是由模拟神经元组成,生物神经元和人工神经元对照关系如下表1所示。树突对应着人工神经元的输入层,细胞体对应于人工神经网络的加权和,而轴突在人工神经网络中为阈值函数,突触为人工神经元的输出层。
表1 人工神经元和人工神经网络关系对照表
| 生物神经元 |
人工神经元 |
作用 |
| 树突 |
输入层 |
接收输入的信号(数据) |
| 细胞体 |
加权和 |
加工和处理信号(数据) |
| 轴突 |
阈值函数 |
控制输出 |
| 突触 |
输出层 |
输出结束 |
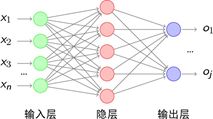
在真正使用时,人工神经网络又被抽象为三层,一是输入层,二是隐含层,三是输出层,其结构如下图2所示。这里的输入层不再是单个神经元的输入,而是要求解问题的输入,比如我们人要拿起桌上的水杯,这个过程不是一个神经元参与的结果,而是多个神经元的协作过程。拿起水杯就是输入层,同时每个神经元也有自己对应的输入。隐含层就是这中间的一系列结果,隐含层的层数就代表了神经元的层数。输出的结果就是我们拿起了桌上的水杯。一般的人工神经网络,只包含很少的隐含层数量,即它的网络比较简单。
图2 人工神经网络三层结构
神经网络在运用之前需要经历一个学习训练过程。目的是通过学习不断地调整和修正网络参数。神经网络的学习包括学习方法和学习规则两个方面的内容。
1、学习方法
神经网络的学习方法主要有多种,按照有无监督来分类,可以分为有监督学习或称有指导学习、无监督学习或称无指导学习以及再励学习。
(1)有监督学习方式中,网络的输出与期望的输出进行比较,然后根据两者的差异调整网络的权重,最终使差异变小。监督即指训练数据本身,不但包括输入数据,还包括一定输入条件下的输出。
(2)无监督学习方式中,输入模式进入网络之后,网络按照一预先设定的规则,如竞争规则等自动调整权重,使网络最终具有模式分类等功能。无监督的学习过程指训练数据只有输入而没有输出,网络必须根据一定的判断标准进行自定调整权重。
(3)再励学习是基于两者之间的一种学习方法。
2、学习规则
神经网络的学习规则主要有以下7种:
(1)Hebb学习跪着
(2)Delta学习跪着
(3)梯度下降学习规则
(4)Kohonen学习规则
(5)后向传播学习规则
(6)概率式学习规则
(7)竞争式学习规则
这里就不进行具体介绍了,可以查阅相关资料,下面通过一个具体的应用来讲解神经网络的计算。
二、神经网络计算
关于神经网络的计算,以最经典的BP神经网络为例,根据网络结构不同和学习算法的区别,神经网络可以有很多的分类,其中BP神经网络(全称为后向传播学习的前馈型神经网络)最为经典。
如上图2我们看到的那样,这样一个神经网络在进行计算式需要经过如下五个步骤:
(1)初始化网络权重
每个相连的神经元之间都有连接权重w(i,j),这个w(i,j)被初始化为一个很小的随机数(例如-1到1之间等);同时每个神经元又有一个篇置Theta(i),也被初始化为一个随机数。
(2)向前传播
根据输入求出输出,即加权和加上偏置,然后再经过激活函数进行计算,对于激活函数,又有很多的知识,这里就以最经典的Sigmoid函数为例,Sigmoid函数曲线如下图3所示:
![]()
图3 Sigmoid函数曲线图
注:图片来自百度百科
Sigmoid函数表达式如下:
在神经网络中为什么要有激活函数呢?如果没有激活函数仅做加权和处理,那么无论神经网络有多少层,其类似于仅仅只做了一层运算。
在向前传播的过程中,每个神经元的输出公式如下:
(3)反向误差传播
当布奏(2)计算完一轮的输出之后,就需要计算反向误差,可以通过预期输出与当前输出进行比较来得到输出单元的误差,有公式如下:
依次计算最后一个隐含层到第一个隐含层每个神经元的误差。
(4)网络权重与偏置更新
权重更新公式:
偏置更新公式:
其中上算式的l表示学习系数,通过此公式依次更新权重。
(5)结束
对于结束的判定可以有两个条件:
1)迭代次数达到了一定的阈值;
2)误差在可接受范围内。
本来还想举个例子来计算一下神经网络,不过这编辑起来太累人了,先就这样吧,下面看代码,hhhh。
三、神经网络编程
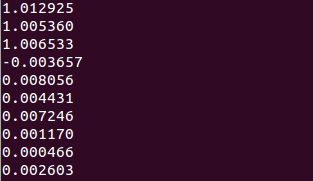
测试样例为一个分类问题,使用BP神经网络,以有监督学习方式,通过in.txt以及out.txt中的数据训练出分类模型,然后再对给定数据进行判定他们的类别,给定数据直接在main.c中了,最后运行结果见末尾图片。在1的附近则表示分类为1,在0附近表示分类为0。
代码以前是在windows下测试的,现在在linux下测试能跑,编译命令gcc xxx.c -o xxx -lm ,直接附代码如下:
#include
#include
#include
#include
#define Data 90
#define In 2
#define Out 1
#define Neuron 25
#define TrainC 200000
#define A 0.2
#define B 0.5
#define a 0.2
#define b 0.4
double d_in[Data][In],d_out[Data][Out];
double w[Neuron][In],o[Neuron],v[Out][Neuron];
double Maxin[In],Minin[In],Maxout[Out],Minout[Out];
double OutputData[Out];
double dv[Out][Neuron],dw[Neuron][In];
double e;
void readData(){
FILE *fp1,*fp2;
int i,j;
if((fp1=fopen("in.txt","r"))==NULL){
printf("can not open the in file\n");
exit(0);
}
for(i=0;id_in[j][i]?Maxin[i]:d_in[j][i];
Minin[i]=Minin[i]d_out[j][i]?Maxout[i]:d_out[j][i];
Minout[i]=Minout[i]0.01);
}
int main(int argc, char const *argv[])
{
readData();
initBPNework();
trainNetwork();
printf("%lf \n",result(9.854303,1.365116) );
printf("%lf \n",result(7.921057,-1.327587) );
printf("%lf \n",result(8.500757,1.492372) );
printf("%lf \n",result(1.339746,-0.291183) );
printf("%lf \n",result(3.107511,0.758367) );
printf("%lf \n",result(2.609525,0.902979) );
printf("%lf \n",result(3.263585,1.367898) );
printf("%lf \n",result(2.912122,-0.202359) );
printf("%lf \n",result(1.731786,0.589096) );
printf("%lf \n",result(2.387003,1.573131) );
writeNeuron();
return 0;
} 在linux下用GCC编译需要加参数 -lm
采用有监督的学习方法进行分类,数据集如下,包含in.txt以及out.txt,拷贝到与程序同一目录即可。
in.txt:
3.542485 1.977398
3.018896 2.556416
7.55151 -1.58003
2.114999 -0.004466
8.127113 1.274372
7.108772 -0.986906
8.610639 2.046708
2.326297 0.265213
3.634009 1.730537
0.341367 -0.894998
3.125951 0.293251
2.123252 -0.783563
0.887835 -2.797792
7.139979 -2.329896
1.696414 -1.212496
8.117032 0.623493
8.497162 -0.266649
4.658191 3.507396
8.197181 1.545132
1.208047 0.2131
1.928486 -0.32187
2.175808 -0.014527
7.886608 0.461755
3.223038 -0.552392
3.628502 2.190585
7.40786 -0.121961
7.286357 0.251077
2.301095 -0.533988
-0.232542 -0.54769
3.457096 -0.082216
3.023938 -0.057392
8.015003 0.885325
8.991748 0.923154
7.916831 -1.781735
7.616862 -0.217958
2.450939 0.744967
7.270337 -2.507834
1.749721 -0.961902
1.803111 -0.176349
8.804461 3.044301
1.231257 -0.568573
2.074915 1.41055
-0.743036 -1.736103
3.536555 3.96496
8.410143 0.025606
7.382988 -0.478764
6.960661 -0.245353
8.23446 0.701868
8.168618 -0.903835
1.534187 -0.622492
9.229518 2.066088
7.886242 0.191813
2.893743 -1.643468
1.870457 -1.04042
5.286862 -2.358286
6.080573 0.418886
2.544314 1.714165
6.016004 -3.753712
0.92631 -0.564359
0.870296 -0.109952
2.369345 1.375695
1.363782 -0.254082
7.27946 -0.189572
1.896005 0.51508
8.102154 -0.603875
2.529893 0.662657
1.963874 -0.365233
8.132048 0.785914
8.245938 0.372366
6.543888 0.433164
-0.236713 -5.766721
8.112593 0.295839
9.803425 1.495167
1.497407 -0.552916
1.336267 -1.632889
9.205805 -0.58648
1.966279 -1.840439
8.398012 1.584918
7.239953 -1.764292
7.556201 0.241185
9.015509 0.345019
8.266085 -0.230977
8.54562 2.788799
9.295969 1.346332
2.404234 0.570278
2.037772 0.021919
1.727631 -0.453143
1.979395 -0.050773
8.092288 -1.372433
1.667645 0.239204out.txt:
0
0
1
0
1
1
1
0
0
0
0
0
0
1
0
1
1
0
1
0
0
0
1
0
0
1
1
0
0
0
0
1
1
1
1
0
1
0
0
1
0
0
0
0
1
1
1
1
1
0
1
1
0
0
1
1
0
1
0
0
0
0
1
0
1
0
0
1
1
1
0
1
1
0
0
1
0
1
1
1
1
1
1
1
0
0
0
0
1
0运行分类结果:
参考文献
[1]张军,詹志辉. 计算智能[M]. 清华大学出版社,2009.11