【PyG学习入门】一：入门使用

简介

首先说一下这个东西，全名是PyTorch-Geometric，是一个PyTorch基础上的一个库，专门用于图形式的数据，可以加速图学习算法的计算过程，比如稀疏化的图等。在学习PyG的各个大的分支之前，先看一下官方文档给出的学习例子。参考链接：

https://pytorch-geometric.readthedocs.io/en/latest/notes/introduction.html

此处直接进行使用的说明，安装过程文档中给出了方式，个人感觉Ubuntu安装会简单一点，但是没有安装过，本人在Windows10安装的，一些依赖库通过VS2019编译，至于为什么不用编译好的wheel文件安装，是因为电脑安装的是Python3.7，大部分编译好的文件都是py36的，所以只能自己编译了。提示一下，windows10编译库的时候过程不是很顺序，出现了很多VS编译的问题。

样例

根据PyG的一些功能函数给出了自带的五个例子，分别为：
（1）图数据处理–Data Handling of Graphs
（2）通用的数据集–Common Benchmark Datasets
（3）小批次–Mini-batches
（4）数据转换–Data Transforms
（5）图上的学习方法–Learning Methods on Graphs

1.Data Handling of Graphs

图（Graph）往往用来表示节点之间成对的关系（也就是边），一个图在PyG中会被定义为torch_geometric.data.Data类的一个实例，常见的类属性如下：

• data.x 节点的特征矩阵，大小为[num_nodes, num_node_features]。
• data.edge_index图中的边的信息，采用COO格式记录，大小为[2, num_edges]，类型为torch.long。COO格式也就是Coordinate Format，采用三元组进行存储，三元组内元素分别为行坐标、列坐标和元素值，此处没有元素值，所以只有2行，num_edges列，每一列表示一个元素。
• data.edge_attr边的特征矩阵，大小为[num_edges, num_edge_features]
• data.y训练目标，允许任意形状，比如节点级别的为[num_nodes, *]，图级别的为[1, *]
• data.pos节点的位置矩阵，大小为[num_node, num_dimensions]
  以上属性都不是必须的，而且可以进行属性拓展，上述的属性用于二维图中，如果对于三维网格数据，可以增加属性data.face，大小为[3, num_faces]，同样为COO格式。
  举一个简单的例子，边上没有权重，无向图（定义边的时候需要两对索引），如下：
  

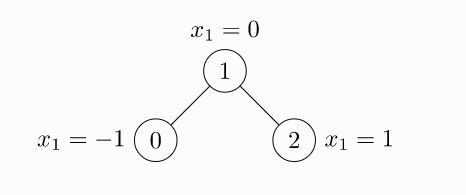
import torch
from torch_geometric.data import Data

# 节点不一定从0开始
edge_index = torch.tensor([
    [3, 1, 1, 2],
    [1, 3, 2, 1]],dtype=torch.long)
# 注意x是二维的，不是一维的，每一行代表一个节点的特征向量，此处特征维度为1
x = torch.tensor([[-1],
                  [0],
                  [1]], dtype=torch.float)

data = Data(x=x, edge_index=edge_index)
print(data)

输出为

Data(edge_index=[2, 4], x=[3, 1])

这里表示的都是维度。如果边数据不是通过COO方式给出的，而是通过节点对方式给出的，需要先转置t()再利用函数contiguous()：

# 通过节点对的方式给出
edge_index = torch.tensor([
    [0, 1], [1, 0], [1, 2], [2, 1]
], dtype=torch.long)
data = Data(x=x, edge_index=edge_index.t().contiguous())
print(data)

两次输出data一致。除此之外，还提供了一部分实用的函数接口：

# 输出data的属性关键字，只有传递参数的才会被输出
print(data.keys)
# ['x', 'edge_index']

# 按照关键字进行输出，注意是字符串
print(data['x'])
# tensor([[-1.],
#         [ 0.],
#         [ 1.]])
print(data['edge_index'])
# tensor([[0, 1, 1, 2],
#         [1, 0, 2, 1]])

print('edge_attr: ', data['edge_attr'])
# edge_attr:  None

# 遍历所有关键字及其对应的数值
for key, item in data:
    print(key, '---', item)

# 可以直接检索key，也可以检索data内函数
if 'edge_attr' not in data.keys:
    print('Not in')
    # Not in

if 'x' in data:
    print('In')
    # In

# print(type(data.keys))
# 

print(data.num_nodes)
# 3

# 这里的边数为4
print(data.num_edges)
# 4

print(data.num_edge_features)
# 0

print(data.num_node_features)
# 1

print(data.contains_isolated_nodes())
# False

print(data.contains_self_loops())
# False

print(data.is_undirected())
# True

上面有个地方需要注意：
在输出keys的时候是没有edge_attr的，但是可以直接访问data['edge_attr']并且得到返回值为None。于是分析一下Data类的源码：

def __init__(self, x=None, edge_index=None, edge_attr=None, y=None,
              pos=None, norm=None, face=None, **kwargs):
     self.x = x
     self.edge_index = edge_index
     self.edge_attr = edge_attr
     self.y = y
     self.pos = pos
     self.norm = norm
     self.face = face

首先上面的代码块，可以看到一开始所有的属性都被初始化参数值，而参数的默认值为None。

def __getitem__(self, key):
    r"""Gets the data of the attribute :obj:`key`."""
    return getattr(self, key, None)

通过重载上面的函数，使得类的对象变为可迭代对象，此时，可以通过data['XXX']访问。此时就明白了为什么可以通过对象访问到edge_attr并且为None。但是为什么从keys中无法获得呢？

    @property
    def keys(self):
        r"""Returns all names of graph attributes."""
        keys = [key for key in self.__dict__.keys() if self[key] is not None]
        keys = [key for key in keys if key[:2] != '__' and key[-2:] != '__']
        return keys

此处进行一个if self[key] is not None判断。并且需要注意的是Data类的很多函数都被@property修饰。此时，对Data类的使用方式有了一个大致了解，但是此时出现一个疑惑，data中的x的顺序和节点大小顺序是对应的么？是不是x的第一个特征向量就是对应最小编号节点的特征向量呢？这个问题暂时还不能解决，等后面再说。

2.Common Benchmark Datasets

这个库中包含了很多数据集，比如Cora、Citeseer、Pubmed以及图分类数据集等等（详情见文档）。直接对数据集进行初始化，初始化的时候就会自动下载其原始文件并转换为Data格式，以数据集ENZYMES 为例，其中包含600个图分为6类：

from torch_geometric.datasets import TUDataset

dataset = TUDataset(root='data/', name='ENZYMES')
print(dataset)
# ENZYMES(600)

第一次下载需要一点时间，第二次运行就不会下载覆盖了，速度比较快。进行一些测试：

print(type(dataset))
# 
print(len(dataset))
# 600
print(dataset.num_node_features)
# 3

如果下载比较慢，可以找到链接手动下载，链接位置在TUDataset中实现：

url = ('https://ls11-www.cs.tu-dortmund.de/people/morris/'
           'graphkerneldatasets')
cleaned_url = ('https://raw.githubusercontent.com/nd7141/'
                'graph_datasets/master/datasets')

然后取消掉下载过程（这里的内容以后在单独更新一篇文章仔细说），手动调用制作数据集的函数：

def process(self):

每一个元素都是一个Data实例：

# dataset是一个可迭代对象，并且每一个元素都是一个Data实例，但是y是一个单独的元素，所以说这个数据集是Graph-level的
data = dataset[0]
print(data)
# Data(edge_index=[2, 168], x=[37, 3], y=[1])

数据集切分可以用切片或者tensor：

# 数据集切分
dataset_train = dataset[:500]
dataset_test = dataset[500:]
print(dataset_train, dataset_test)
# ENZYMES(500) ENZYMES(100)
dataset_sample1 = dataset[torch.tensor([i for i in range(500)], dtype=torch.long)]
print(dataset_sample1)
# ENZYMES(500)
dataset_sample2 = dataset[torch.tensor([True, False])]
print(dataset_sample2)
# ENZYMES(1)
print(dataset[0])
# Data(edge_index=[2, 168], x=[37, 3], y=[1])
print(dataset[1])
# Data(edge_index=[2, 102], x=[23, 3], y=[1])
print(dataset_sample2[0])
# Data(edge_index=[2, 168], x=[37, 3], y=[1])

布尔型tensor类似一个滤波器，但是是从头开始的。打乱操作如下：

dataset = dataset.shuffle()
# 等价于
dataset = dataset[torch.randperm(len(dataset))]

下面的函数返回长度为n，范围为0~n-1的一种全排列tensor：

torch.randperm()

官方文档还给出了一个cora数据集的例子，特别的地方在于：

data.train_mask.sum().item()

cora数据集在Data类中额外添加了几个属性，比如train_mask，通过sum函数可以得到train训练集的总数，之所以可以自己定义新的属性，因为：

def __init__(self, x=None, edge_index=None, edge_attr=None, y=None,
             pos=None, norm=None, face=None, **kwargs):

Data类给了一个**kwargs。

3.Mini-batches

神经网络通常会按照batch方式进行训练，PyG通过构建稀疏化的分块对角阵实现mini-batch的并行化，构建方式按照每一个Data实例的edge_index构建一个Graph的邻接矩阵，然后将所有节点的特征向量按行拼接，目标值同理。这也就使得即使一个batch内部的图是不同结构的，也可以一起训练。

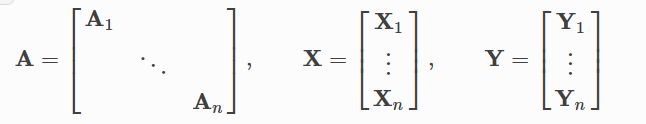
通过DataLoader函数进行batch的构造：

from torch_geometric.datasets import TUDataset
from torch_geometric.data import DataLoader

dataset = TUDataset(root='data/', name='ENZYMES', use_node_attr=True)
loader = DataLoader(dataset, batch_size=32, shuffle=True)

for batch in loader:
    print(batch)
    # Batch(batch=[1005], edge_index=[2, 3948], x=[1005, 21], y=[32])
    

一个batch为32个图，但是每一个图的规模是不一样的，如上案例，第一个batch内的32个图共1005节点，含有3948条边。torch_geometric.data.Batch继承自torch_geometric.data.Data，并且添加了一个额外的属性batch。batch是一个列向量，代表了每一个节点对应到哪一个图。

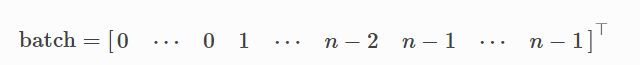
利用另一个库torch-scatter可以对图信息进行一些计算，比如：

from torch_geometric.datasets import TUDataset
from torch_geometric.data import DataLoader
from torch_scatter import scatter_mean

dataset = TUDataset(root='data/', name='ENZYMES', use_node_attr=True)
loader = DataLoader(dataset, batch_size=32, shuffle=True)

for data in loader:
    print(data)
    # Batch(batch=[1005], edge_index=[2, 3948], x=[1005, 21], y=[32])
    x = scatter_mean(data.x, data.batch, dim=0)
    print(x.size())
    # torch.Size([32, 21])

此处以每一个图为单位，将各个图中的所有节点的特征向量计算了一个平均值，所以维度为[32, 21]。

4.Data Transforms

（本模块个人使用场景不多，暂时不展开描述）
以ShapeNet数据集为例，进行测试，数据集有17000个3D点云，并且每一个点的类别为16类中的一个：

from torch_geometric.datasets import ShapeNet

dataset = ShapeNet(root='data/ShapeNet', categories=['Airplane'])
print(dataset[0])
# Data(pos=[2518, 3], y=[2518])

注意：应该在数据集存储到磁盘之前进行pre_transform，这会使得加载速度更快，也就是在第一次下载时进行转换，此时下一次初始化数据集的时候，就会调用转换后的数据集（即使下一次的调用没有指定pre_transform参数）。

5.Learning Methods on Graphs

重要到了比较重要的地方了，也就是如何构建一个模型。这里选择搭建一个简单的GCN模型，并通过Cora数据集进行测试。
首先构建一个两层的GCN：

# 继承torch的类
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = GCNConv(dataset.num_node_features, 16)
        self.conv2 = GCNConv(16, dataset.num_classes)
        
    def forward(self, data):
        x, edge_index = data.x, data.edge_index
        
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)
        
        return F.log_softmax(x, dim=1)

注意得是在GCNConv中没有自带非线性处理过程，训练过程和测试过程如下：

if __name__ == '__main__':
    # 加载数据集
    dataset = Planetoid(root='data/', name='Cora')
    #　Train
    device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
    model = Net().to(device)
    data = dataset[0].to(device)
    optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)

    model.train()
    for epoch in range(200):
        optimizer.zero_grad()
        out = model(data)
        loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
        loss.backward()
        optimizer.step()

    # Test
    model.eval()
    _, pred = model(data).max(dim=1)
    correct = float(pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())
    acc = correct / data.test_mask.sum().item()
    print('Accuracy: {:.4f}'.format(acc))