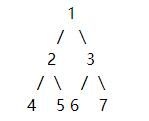数据结构与算法(C++)——二叉树的遍历
二叉树的遍历
二叉树是一种重要的数据结构。遍历方式有前序遍历、中序遍历、后续遍历以及层次遍历。对于前序、中序和后续遍历,采用递归的思想代码实现起来简单且容易理解,非递归实现需要用到辅助栈。层次遍历需要用到辅助队列来实现。
一、前序遍历
前序遍历是按照:根结点-左结点-有结点 顺序访问。
递归代码实现:
/*二叉树前序遍历递归实现*/
void preOrder(BinaryTreeNode* Root)
{
if (Root != NULL)
{
cout << Root->val << " ";
preOrder(Root->left);
preOrder(Root->right);
}
}对于任一结点p:
(1)访问结点P,并将结点P入栈;
(2)判断结点P的左结点是否为空,若为空,则取栈顶元素并进行出栈操作,并将栈顶元素的右结点置为当前P,重复(1);若不为空,则将P的左结点置为当前P;
(3)直到P为NULL并且栈为空,则遍历结束。
代码实现:
/*二叉树前序遍历非递归实现1*/
void preOrder_1(BinaryTreeNode* Root)
{
if (Root == NULL)
return;
stack nodeStack;
nodeStack.push(Root);
while (!nodeStack.empty())
{
BinaryTreeNode* p = nodeStack.top();
nodeStack.pop();
cout << p->val << " ";
if (p->right != NULL)
nodeStack.push(p->right);
if (p->left != NULL)
nodeStack.push(p->left);
}
}
/*二叉树前序遍历非递归实现2*/
void preOrder_2(BinaryTreeNode* Root)
{
if (Root == NULL)
return;
stack nodeStack;
BinaryTreeNode* p = Root;
while (p != NULL || !nodeStack.empty())
{
while (p != NULL)
{
cout << p->val << " ";
nodeStack.push(p);
p = p->left;
}
if (!nodeStack.empty())
{
p = nodeStack.top();
nodeStack.pop();
p = p->right;
}
}
} 中序遍历是按照:左结点-根结点-右结点 顺序访问。
递归代码实现:
/*二叉树中序遍历递归实现*/
void inOrder(BinaryTreeNode* Root)
{
if (Root != NULL)
{
inOrder(Root->left);
cout << Root->val << " ";
inOrder(Root->right);
}
}对于任一结点P:
(1)若P的左结点不为空,则将P入栈并将P的左结点置为当前P,重复这个操作;
(2)若P的左结点为NULL,则取栈顶元素并进行出栈操作,访问该栈顶元素,然后将栈顶元素的右结点置为当前结点P;
(3)直到P为NULL并且栈为空,则遍历结束。
代码实现:
/*二叉树中序遍历递归实现*/
void inOrder_1(BinaryTreeNode* Root)
{
if (Root == NULL)
return;
stack nodeStack;
BinaryTreeNode* p = Root;
while (p != NULL || !nodeStack.empty())
{
while (p != NULL)
{
nodeStack.push(p);
p = p->left;
}
if (!nodeStack.empty())
{
p = nodeStack.top();
cout << p->val << " ";
nodeStack.pop();
p = p->right;
}
}
} 后续遍历是按照:左结点-右结点-根结点 顺序访问。
递归代码实现:
/*二叉树后续遍历递归实现*/
void postOrder(BinaryTreeNode* Root)
{
if (Root != NULL)
{
postOrder(Root->left);
postOrder(Root->right);
cout << Root->val << " ";
}
}后序遍历的非递归实现是三种遍历方式中最难的一种。因为在后序遍历中,要保证左孩子和右孩子都已被访问并且左孩子在右孩子前访问才能访问根结点,这就为流程的控制带来了难题。因此要保证根结点在其左结点和右结点都被访问完以后才能被访问。
对于任一结点P:
(1)将结点P入栈;
(2)如果结点P的左结点和右结点都为NULL或者P的左结点和右结点都已经被访问过,则访问P结点;
(3)若不满足(2)则将P的右结点和左结点依次入栈,重复(2);
(4)直到栈为空,则遍历结束。
代码实现:
/*二叉树后续遍历非递归实现*/
void postOrder_1(BinaryTreeNode* Root)
{
if (Root == NULL)
return;
stack nodeStack;
BinaryTreeNode* cur = NULL;
BinaryTreeNode* pre = NULL;
nodeStack.push(Root);
while (!nodeStack.empty())
{
cur = nodeStack.top();
if ((cur->left == NULL&&cur->right == NULL) || (pre != NULL && (pre == cur->left || pre == cur->right)))
{
cout << cur->val << " ";
nodeStack.pop();
pre = cur;
}
else
{
if (cur->right != NULL)
nodeStack.push(cur->right);
if (cur->left != NULL)
nodeStack.push(cur->left);
}
}
}
层次遍历顺序为:从上到下、从左到右 的顺序访问。
层次遍历需要用辅助栈来保存接下来需要访问的结点。
对于任一结点P:
(1)如果P不为NULL,将结点P入队;
(2)取队头元素并进行出队操作,访问队头元素,如果队头元素的左结点或右结点不为空,则将其左结点或右结点入队,重复这个操作;
(3)直到队列为空,则遍历结束。
代码实现:
/*二叉树层次遍历*/
void levelsOrder(BinaryTreeNode* Root) {
if (Root == NULL)
return;
queue queTreeNode; //队列存储遍历的二叉树节点
queTreeNode.push(Root);
while (queTreeNode.size())
{
BinaryTreeNode *pNode = queTreeNode.front();
queTreeNode.pop();
cout << pNode->val << " ";
if (pNode->left)
queTreeNode.push(pNode->left);
if (pNode->right)
queTreeNode.push(pNode->right);
}
}
#include
#include
#include
using namespace std;
struct BinaryTreeNode
{
int val;
BinaryTreeNode* left;
BinaryTreeNode* right;
BinaryTreeNode(int x):val(x),left(NULL),right(NULL){}
};
class Solution {
public:
/*二叉树前序遍历递归实现*/
void preOrder(BinaryTreeNode* Root)
{
if (Root != NULL)
{
cout << Root->val << " ";
preOrder(Root->left);
preOrder(Root->right);
}
}
/*二叉树前序遍历非递归实现*/
void preOrder_2(BinaryTreeNode* Root)
{
if (Root == NULL)
return;
stack nodeStack;
BinaryTreeNode* p = Root;
while (p != NULL || !nodeStack.empty())
{
while (p != NULL)
{
cout << p->val << " ";
nodeStack.push(p);
p = p->left;
}
if (!nodeStack.empty())
{
p = nodeStack.top();
nodeStack.pop();
p = p->right;
}
}
}
//===================================================================
/*二叉树中序遍历递归实现*/
void inOrder(BinaryTreeNode* Root)
{
if (Root != NULL)
{
inOrder(Root->left);
cout << Root->val << " ";
inOrder(Root->right);
}
}
/*二叉树中序遍历非递归实现*/
void inOrder_1(BinaryTreeNode* Root)
{
if (Root == NULL)
return;
stack nodeStack;
BinaryTreeNode* p = Root;
while (p != NULL || !nodeStack.empty())
{
while (p != NULL)
{
nodeStack.push(p);
p = p->left;
}
if (!nodeStack.empty())
{
p = nodeStack.top();
cout << p->val << " ";
nodeStack.pop();
p = p->right;
}
}
}
//=====================================================
/*二叉树后续遍历递归实现*/
void postOrder(BinaryTreeNode* Root)
{
if (Root != NULL)
{
postOrder(Root->left);
postOrder(Root->right);
cout << Root->val << " ";
}
}
/*二叉树后续遍历非递归实现*/
void postOrder_1(BinaryTreeNode* Root)
{
if (Root == NULL)
return;
stack nodeStack;
BinaryTreeNode* cur = NULL;
BinaryTreeNode* pre = NULL;
nodeStack.push(Root);
while (!nodeStack.empty())
{
cur = nodeStack.top();
if ((cur->left == NULL&&cur->right == NULL) || (pre != NULL && (pre == cur->left || pre == cur->right)))
{
cout << cur->val << " ";
nodeStack.pop();
pre = cur;
}
else
{
if (cur->right != NULL)
nodeStack.push(cur->right);
if (cur->left != NULL)
nodeStack.push(cur->left);
}
}
}
//==========================================================
/*二叉树层次遍历*/
void levelsOrder(BinaryTreeNode* Root) {
if (Root == NULL)
return;
queue queTreeNode; //队列存储遍历的二叉树节点
queTreeNode.push(Root);
while (queTreeNode.size())
{
BinaryTreeNode *pNode = queTreeNode.front();
queTreeNode.pop();
cout << pNode->val << " ";
if (pNode->left)
queTreeNode.push(pNode->left);
if (pNode->right)
queTreeNode.push(pNode->right);
}
}
};
int main()
{
BinaryTreeNode Root(1);
BinaryTreeNode TreeNode2(2);
BinaryTreeNode TreeNode3(3);
BinaryTreeNode TreeNode4(4);
BinaryTreeNode TreeNode5(5);
BinaryTreeNode TreeNode6(6);
BinaryTreeNode TreeNode7(7);
Root.left = &TreeNode2;
Root.right = &TreeNode3;
TreeNode2.left = &TreeNode4;
TreeNode2.right = &TreeNode5;
TreeNode3.left = &TreeNode6;
TreeNode3.right = &TreeNode7;
Solution s;
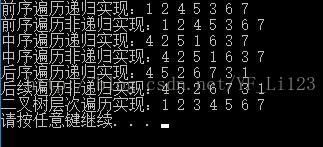
cout << "前序遍历递归实现:";
s.preOrder(&Root);
cout << endl << "前序遍历非递归实现:";
s.preOrder_2(&Root);
cout << endl << "中序遍历递归实现:";
s.inOrder(&Root);
cout << endl << "中序遍历非递归实现:";
s.inOrder_1(&Root);
cout << endl << "后序遍历递归实现:";
s.postOrder(&Root);
cout << endl << "后续遍历非递归实现:";
s.postOrder_1(&Root);
cout << endl<<"二叉树层次遍历实现:";
s.levelsOrder(&Root);
cout << endl;
return 0;
}