机器学习python实现（一）：多元线性回归

在这一部分中，你将用多元线性回归来预测房价。假设你正在出售你的房子，你想知道一个好的市场价格是什么。一种方法是首先收集最近出售的房屋的信息，并建立房价模型。文件ex1data2.txt包含俄勒冈州波特兰的房价培训集。第一列是房子的大小(以平方英尺为单位)，第二栏是卧室的数量，第三栏是房子的价格。
一 多元线性回归
1-1 多元方程
多元线性回归指的就是有多个X的情况。比如与房价y有关的变量有：房屋面积x1，位置x2。

此时，我们就要把我们的方程 hθ(x)=θ0+θ1∗x 修改为：

hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn
其实本质并没有变，就是变量x多了，所以参数θ也跟着多了。但是思想还是没有变：通过误差函数，经过梯度下降求参数。

为了结构统一，我们设 x0=1 ；此时方程应为：

hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn=θTx

如此一来，便将变量向量化了。也变得和第一章的一样了。

import matplotlib.pyplot as plt
import numpy as np
#导入数据
data=np.loadtxt('ex1data2.txt',delimiter=',',dtype=np.int64)
data=np.matrix(data)
X=data[:,0:2]
y=data[:,2]
m=y.size
X=np.c_[np.ones(m),X]
theta=np.matrix([0,0,0])

part1:特征归一化
通过查看这些值，注意房子的大小大约是卧室数量的1000倍。当两种变量数值维度相差过大的时候，梯度下降法会迭代得很慢，比如房屋面积X1都是100多平米，楼层都是1、2、3这样的数字，两种特征就相差很大。在这种情况下， 我们可以通过使每个输入值在大致相同的范围内来加速梯度下降。（−1 ≤ x(i) ≤ 1）
特征归一化：
（1）从数据集中减去每个特征的平均值。
（2）减去平均值后，再用它们各自的“标准差”除以特征值。

#定义特征归一化函数
def feature_normalize(X):
    X_norm=(X[:,:]-np.mean(X[:,:]))/np.std(X[:,:])   #使用“std”函数来计算标准差
    return X_norm
   
X=feature_normalize(X)    #将X中的数据特征归一化

1-2 代价函数与梯度下降

梯度下降的方法也没有变，重复直到即可。

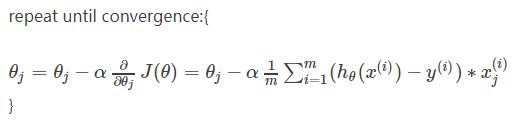
part2:代价函数与梯度下降

#定义代价函数
def compute_cost(X, y, theta):
    inner = np.power(((X * theta.T) -  y), 2)
  #  inner = ((X * theta.T) -  y).T*((X * theta.T) -  y)
    return np.sum(inner) / (2 * len(X))

#定义梯度下降函数
def gradient_descent_multi(X,y,theta,alpha,num_iters):
     m=y.size
     J_history=np.zeros(num_iters)
     
     
     for i in range(0,num_iters):
         theta=theta-(alpha/m)*((X*theta.T-y).T*X)
         J_history[i]=compute_cost(X,y,theta)
     return theta,J_history

alpha=0.001  #学习率
num_iters=4000  #迭代次数
theta,J_history=gradient_descent_multi(X,y,theta,alpha,num_iters)

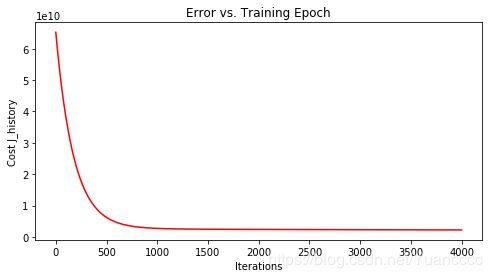
需要注意的是，对于不同的问题，梯度下降收敛所需的迭代次数也不同。我们很难确定地说出在第几次迭代算法收敛，因此，我们常常需要J(θ)随迭代次数变化的曲线图帮忙判断。
part3:代价函数和迭代次数的关系

fig1 = plt.figure(3)
fig, ax = plt.subplots(figsize=(8,4))
ax.plot(np.arange(num_iters), J_history, 'r')  # np.arange()返回等差数组
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost J_history')
ax.set_title('Error vs. Training Epoch')
plt.show()  

运行结果：

二 正规方程
除了梯度下降法，另一种求最小值的方式则是让代价函数导数为0，求θ值 。即：

使用此公式不需要任何特征缩放，您将在一次计算中得到精确的解：在收敛之前不存在类似于梯度下降的“循环”。请记住，我们仍然需要在X矩阵中添加1的列，才能有一个截距项(θ0)。
part4：用正规方程求theta

import matplotlib.pyplot as plt
import numpy as np

data=np.loadtxt('ex1data2.txt',delimiter=',',dtype=np.int64)
data=np.matrix(data)
X=data[:,0:2]
y=data[:,2]

X=np.c_[np.ones(y.size),X]

# 定义正规方程
def normalEqn(X, y):   
    theta =( np.linalg.inv(X.T*X))*X.T*y
    return theta
    
theta=normalEqn(X,y)
print(theta)

总体来说：
（1）正规方程计算巧妙，但不一定有效。
（2）梯度下降法速度慢，但是稳定可靠。
通常，n在10000以下时，正规方程法会是一个很好的选择，而当n>10000时，多考虑用梯度下降法。