A*算法实验
一、实验目的:
熟悉和掌握启发式搜索的定义、估价函数和算法过程,并利用A*算法求解N数码难题,理解求解流程和搜索顺序。
二、实验原理:
A*算法是一种有序搜索算法,其特点在于对估价函数的定义上。对于一般的有序搜索,总是选择f值最小的节点作为扩展节点。因此,f是根据需要找到一条最小代价路径的观点来估算节点的,所以,可考虑每个节点n的估价函数值为两个分量:从起始节点到节点n的代价以及从节点n到达目标节点的代价。
三、我的报告
理解
我对A*算法的理解,采用回溯法加贪心算法的方式去搜索图中两个点的最短路径。可以在绕过障碍物的情况,求最短路径。
借用几个图:
贪心的依据:
f = g + h ;
g;当前点到原点的距离,正方形上下左右距离是1,左上角这1.4(根号2)
h:当前点到目标点的距离,求法是:终点与当前点的横坐标差+终点与当前点的纵坐标差。
回溯:
遇到障碍物我们就不计算,但是如果发现周围节点的路径我走过的,那我就要忽略掉他。
代码实现
//三数据结构
package ai.a;
import java.util.Objects;
/**
* @Author: WYF
* @Description: 坐标,实现了比较方法
* @Create: 2020/4/15 10:55
* @Version: 1.0
*/
public class Coord {
public int x;
public int y;
public Coord(int x, int y) {
this.x = x;
this.y = y;
}
/**
* @Description: 重写equel和hashCode方法,可以实现比较
*/
@Override
public boolean equals(Object o) {
if (this == o) {
return true;
}
if (o == null || getClass() != o.getClass()) {
return false;
}
Coord coord = (Coord) o;
return x == coord.x &&
y == coord.y;
}
@Override
public int hashCode() {
return Objects.hash(x, y);
}
}
package ai.a;
/**
* @Author: WYF
* @Description: 封装更完整的节点,包括本身坐标数据,G和H和父节点。
* @Create: 2020/4/15 10:59
* @Version: 1.0
*/
public class Node implements Comparable<Node> {
/** 坐标*/
public Coord coord;
/** 父结点*/
public Node parent;
/** G:是个准确的值,是起点到当前结点的代价*/
public int G;
/** H:是个估值,当前结点到目的结点的估计代价*/
public int H;
public Node(int x,int y) {
this.coord = new Coord(x,y);
}
public Node(Coord coord, Node parent, int g, int h) {
this.coord = coord;
this.parent = parent;
G = g;
H = h;
}
/**
* @Description: 比较的是G+H,H是曼哈顿距离,G是节点本身到起始位置的距离
* @Param: [node]
* @Return: int
* @Author: WYF
* @Date: 2020/4/15 11:06
*/
@Override
public int compareTo(Node node) {
if (node == null) {
return -1;
}
if (G+H > node.G+node.H) {
return 1;
}else if (G+H < node.G+node.H) {
return -1;
}
return 0;
}
}
package ai.a;
/**
* @Author: WYF
* @Description: A星算法输入的所有数据,封装在一起,传参方便。
* @Create: 2020/4/15 11:09
* @Version: 1.0
*/
public class MapInfo {
public int[][] maps;
/** 地图宽度 */
public int width;
/** 地图高度 */
public int hight;
public Node start;
public Node end;
public MapInfo(int[][] maps, int width, int hight, Node start, Node end) {
this.maps = maps;
this.width = width;
this.hight = hight;
this.start = start;
this.end = end;
}
}
//2测试类:
package ai.a;
/**
* @Author: WYF
* @Description: 测试类
* @Create: 2020/4/15 11:13
* @Version: 1.0
*/
public class Test {
public static void main(String[] args)
{
int[][] maps = {
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 }
};
MapInfo info=new MapInfo(maps,maps[0].length, maps.length,new Node(1, 1), new Node(4, 5));
new AStar().start(info);
printMap(maps);
}
/**
* @Description: 打印地图
* @Param: [maps]
* @Return: void
* @Author: WYF
* @Date: 2020/4/15 11:13
*/
public static void printMap(int[][] maps)
{
for (int i = 0; i < maps.length; i++)
{
for (int j = 0; j < maps[i].length; j++)
{
System.out.print(maps[i][j] + " ");
}
System.out.println();
}
}
}
//3核心代码实现:
package ai.a;
import java.util.ArrayList;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Queue;
/**
* @Author: WYF
* @Description: 核心,基于前三个类数据结构,实现A*算法
* @Create: 2020/4/15 11:14
* @Version: 1.0
*/
public class AStar {
public final static int BAR = 1; // 障碍值
public final static int PATH = 2; // 路径
/**
* G值需要的横纵移动代价和斜移动代价。10就说1.0,14就说1.4
*/
public final static int DIRECT_VALUE = 10; // 横竖移动代价
public final static int OBLIQUE_VALUE = 14; // 斜移动代价
Queue<Node> openList = new PriorityQueue<Node>(); // 优先队列(升序)
List<Node> closeList = new ArrayList<Node>();
/**
* 判断结点是否是最终结点
*/
private boolean isEndNode(Coord end, Coord coord) {
return coord != null && end.equals(coord);
}
/**
* 判断结点能否放入Open列表(优先队列)
*/
private boolean canAddNodeToOpen(MapInfo mapInfo, int x, int y) {
// 是否在地图中,超过地图大小
if (x < 0 || x >= mapInfo.width || y < 0 || y >= mapInfo.hight) {
return false;
}
// 判断是否是不可通过的结点,该节点是障碍,不能用
if (mapInfo.maps[y][x] == BAR) {
return false;
}
// 判断结点是否存在close表,
if (isCoordInClose(x, y)) {//如果坐标已经在close中,不能再放入open
return false;
}
return true;
}
/**
* 判断坐标是否在close表中,调用与自己重载的方法,多了应该非空判断
*/
private boolean isCoordInClose(Coord coord) {
return coord != null && isCoordInClose(coord.x, coord.y);
}
/**
* 判断坐标是否在close表中,close的list,查看有没有一样的数据
*/
private boolean isCoordInClose(int x, int y) {
if (closeList.isEmpty()) {
return false;
}
for (Node node : closeList) {
if (node.coord.x == x && node.coord.y == y) {
return true;
}
}
return false;
}
/**
* @Description: 计算H值,坐标分别取差值相加
*/
private int calcH(Coord end, Coord coord) {
return Math.abs(end.x - coord.x) + Math.abs(end.y - coord.y);
}
/**
* @Description: 从Open列表中查找结点
*/
private Node findNodeInOpen(Coord coord) {
if (coord == null || openList.isEmpty()) {
return null;
}
for (Node node : openList) {
if (node.coord.equals(coord)) {
return node;
}
}
return null;
}
/**
* 添加所有邻结点到open表
*/
private void addNeighborNodeInOpen(MapInfo mapInfo, Node current) {
int x = current.coord.x;
int y = current.coord.y;
// 左
addNeighborNodeInOpen(mapInfo, current, x - 1, y, DIRECT_VALUE);
// 上
addNeighborNodeInOpen(mapInfo, current, x, y - 1, DIRECT_VALUE);
// 右
addNeighborNodeInOpen(mapInfo, current, x + 1, y, DIRECT_VALUE);
// 下
addNeighborNodeInOpen(mapInfo, current, x, y + 1, DIRECT_VALUE);
// 左上
addNeighborNodeInOpen(mapInfo, current, x - 1, y - 1, OBLIQUE_VALUE);
// 右上
addNeighborNodeInOpen(mapInfo, current, x + 1, y - 1, OBLIQUE_VALUE);
// 右下
addNeighborNodeInOpen(mapInfo, current, x + 1, y + 1, OBLIQUE_VALUE);
// 左下
addNeighborNodeInOpen(mapInfo, current, x - 1, y + 1, OBLIQUE_VALUE);
}
/**
* 添加一个邻结点到open表
*/
private void addNeighborNodeInOpen(MapInfo mapInfo, Node current, int x, int y, int value) {
if (canAddNodeToOpen(mapInfo, x, y)) {
Node end = mapInfo.end;
Coord coord = new Coord(x, y);
int G = current.G + value; // 计算邻结点的G值
Node child = findNodeInOpen(coord);
if (child == null) {
int H = calcH(end.coord, coord); // 计算H值
if (isEndNode(end.coord, coord)) {
child = end;
child.parent = current;
child.G = G;
child.H = H;
} else {
child = new Node(coord, current, G, H);
}
openList.add(child);
} else if (child.G > G) {
child.G = G;
child.parent = current;
// 重新调整堆
openList.add(child);
}
}
}
/**回溯法绘制路径*/
private void drawPath(int[][] maps, Node end) {
if (end == null || maps == null) {
return;
}
System.out.println("总代价:" + end.G);
/** 修改矩阵,把一路上经过的节点赋值为2,表示为路径,是从后往前推的*/
while (end != null) {
Coord c = end.coord;
maps[c.y][c.x] = PATH;
end = end.parent;
}
}
/** 开始算法,循环移动结点寻找路径,设定循环结束条件,Open表为空或者最终结点在Close表*/
public void start(MapInfo mapInfo) {
if (mapInfo == null) {
return;
}
// clean
openList.clear();
closeList.clear();
// 开始搜索
openList.add(mapInfo.start);
moveNodes(mapInfo);
}
/**
* 移动当前结点
*/
private void moveNodes(MapInfo mapInfo) {
while (!openList.isEmpty()) {
Node current = openList.poll();//每次都从优先队列里面去一个最小的值,加入到open中
closeList.add(current);
addNeighborNodeInOpen(mapInfo, current);
if (isCoordInClose(mapInfo.end.coord)) // 是不是终点,是就提出
{
drawPath(mapInfo.maps, mapInfo.end);
break;
}
}
}
}
总结
1.A算法流程图
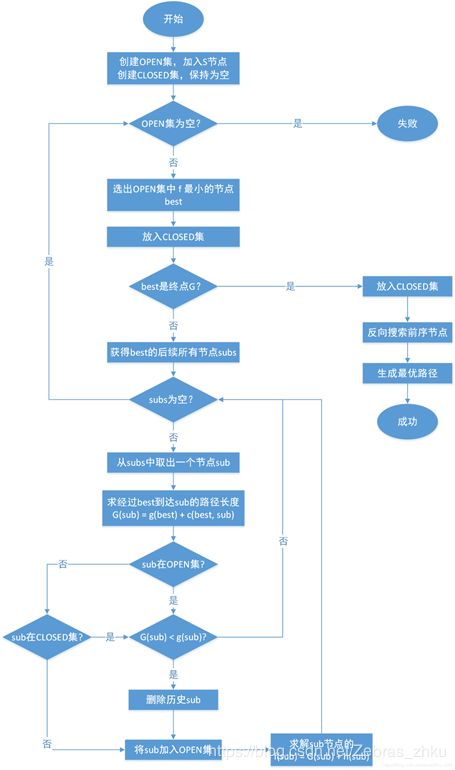
2.试分析估价函数的值对搜索算法速度的影响。
个人理解,每次移动都是贪心的,这样就保证每次距离都最短;但是贪心还不够,再遇到障碍物的情况下,要进行回溯。重新去找节点。这样就实现了绕过障碍物和求得最短路径。
估价函数的形式为:f(n)=g(n)+h(n),g(n)为起点到当前位置的实际路径长度,h(n)为所在位置到终点的最佳路径的估计距离。
这个估算,保证了所找到的路径是最短路径。在我的二维平面地图中,由于我可以沿着对角线行走,所以h(n)为所在位置到终点的直线距离。假如只能上下左右移动,那h*(n)为n到终点的水平距离与垂直距离的和。
3. 根据A*算法分析启发式搜索的特点。
启发式搜索又称为有信息搜索,它是利用问题拥有的启发信息来引导搜索,达到减少搜索范围、降低问题复杂度的目的,这种利用启发信息的搜索过程称为启发式搜索。
上面的例子中:
f(n)=g(n)+h(n)
式中:g(x)为从初始节点到节点x付出的实际代价;h(x)为从节点x到目标节点的最优路径的估计代价。启发性信息主要体现在h(x)中,其形式要根据问题的特性来确定。
虽然启发式搜索有望能够很快到达目标节点,但需要花费一些时间来对新生节点进行评价。因此,在启发式搜索中,估计函数的定义是十分重要的。如定义不当,则上述搜索算法不一定能找到问题的解,即使找到解,也不一定是最优的。
代码和图都是搜索过来,然后总结的,有侵权请联系