贪婪算法有多好？Submodularity告诉你

贪婪算法有多好？Submodularity告诉你

贪婪算法可以说是最符合我们人类直觉的算法了，甚至有的时候贪婪算法就可以得到目标的最优解，比如说最小生成树算法。那么我们自然就会想知道，它能达到最优值吗？如何判断？实际上一个叫Matroid的东西是可以帮助我们判断是否能达到最优值的。但是如果不能达到最优，它到底有多近似呢？submodularity optimization对这个问题给予了一个答案。

我们形式化地定义一下这个贪婪算法的问题，对于元素N，我们希望找到一个使得f最大的最优子集$S\in N$，即$ma{x}_{S\in N}f(S)$，其中$f:2^N\to \mathbb{R}$

这样的问题很显然，我们是不可能去遍历所有的子集来找这个最优解的，所以在什么条件下，这样的问题才可以求解？

submodularity condition

接下来，我们会对f做一些约束，赋予他一个叫monotone和submodularity的性质。我们可以把f想象成是一个评价雷达覆盖范围的函数，当我们在不同的点选择放置雷达的时候，他有可能会跟现有的一些雷达的范围有重合，但是可以肯定的是，当我们在不停放置雷达的时候，覆盖范围是肯定不会减少的，只会变得越来越大。即如果有集合$S\subset T$一定有$f(S)⩽f(T)$这称为monotone 单调性。

因此，单调性是我们希望函数拥有的第一个性质。

而第二个性质就是submodularity性质。

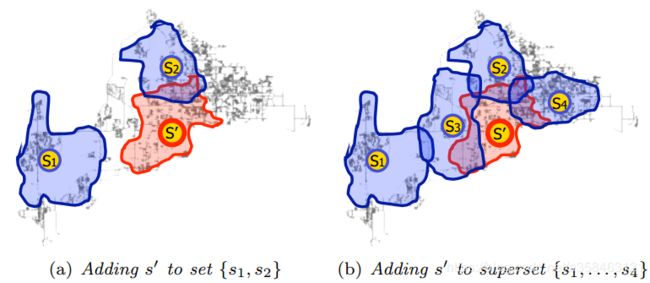
对于同一个地方，在雷达覆盖范围比较小的时候加入一个雷达(左图)，它的效果肯定比在雷达覆盖范围比较大的时候加一个雷达的效果要好(右图)。基于此我们可以给出一个定义：

Definition 1 函数$f:2^N\to \mathbb{R}$成为submodular当且仅当对于所有的子集$S\subset T\subset N$ 和 所有$x\in N\backslash T$
$$f(S\cup \{x\})-f(S)\ge f(T\cup \{x\})-f(T)$$

这里T就是雷达覆盖范围比较大的时候，S就是覆盖范围比较小的时候，显然对S“雪中送炭”的效果要更加好。

Proposition 1 $f是$submodular 当且仅当$A,B\subset N$

$$f(A\cap B)+f(A\cup B)\le f(A)+f(B)$$

证明：令$A=T,B=S\cup \{x\}$这就是我们上面的定义的式子，实际上因为$A\cap B\subset B$根据定义我们可以推出：
$$\begin{gathered} f(A)-f(A\cap B)\ge f(A\cup B)-f(B) \\ f(\{A\cap B\}\cup \{A\})-f(A\cap B)\ge f(B\cup A)-f(B) \end{gathered}$$
在不等号左边，A可以换种写法，是$\{A\cap B\}$然后再并上的A，于是我们就得到上面的这条公式。

接下来再介绍几个有用的性质，submodular函数的求和还是submodular函数，submodular函数的加权求和（权重非负）也还是submodular函数。这个性质让我们可以定义一些很简单的submodular函数，然后把他们加起来组成一个复杂的函数。

Submodularity + Monotonicity = $1-\frac{1}{e}$ approximation.

现在你的函数有了这两个性质，而且任务找到一个大小为k的子集S使得f达到最大，那么不同大小的k会造成什么影响呢？该理论的一个漂亮的地方是，如果你函数有Submodularity和Monotonicity这两个性质那么至少63%的效果是可以保证的。当然在实际中，常常可以高于这个值。以下定理给出了该描述的一个正式证明，该函数在使用贪婪算法，每一步都选择一个最优的元素x来最大化f时，他一定能得到一个1-1/e(63%)的近似。为了证明这个bound，我们给出几个定义以及一些有用的定理。

Definition 2 $f:2^N\to R$,$S\subseteq N$, 对于与S的marginal contribution 定义为一个关于S的函数$f_S$
$$\forall T\subseteq N,f_S(T)=f(S\cup T)-f(S)$$
这个表示在已有集合S的前提下增加一个T的增量。根据submodular的性质，显然submodular等价于$\forall S\subseteq T\subseteq N,\forall e\in N\backslash T$, $f_T(e)⩽f_S(e)$.事实上，这里定义的marginal contribution可以看做是在离散数据上微分的推广，这里测量的正是一种增量。

Proposition 2 以下三个命题是等价的:

1. f is submodular
2. $f_S$ is submodular
3. $f_S$ is subadditive

证明：
1⟹ 2: 设$T\subset M$，于是可以推出下面等式成立：
$$\begin{array}{rl}{f}_S(T\cup e)-f_S(T)& =f(S\cup T\cup e)-f(S)-f(S\cup T)+f(S)\\ & =f(S\cup T\cup e)-f(S\cup T)\\ & \ge f(S\cup M\cup e)-f(S\cup M)=f_S(M\cup e)-f_S(M)\end{array}$$

2⟹3: 由上一个条件可知$f_S$也是submodular函数，因此我们只需证明submodular函数都是subadditive就可以了。
设$B=\{e_1,...,e_n\},B_i=\{e_1,...,e_i\}$
$$\begin{array}{rl}f(A\cup B)& =f(A)+f(A\cup B)-f(A)\\ & =f(A)+\sum _{i=1}^{n}f(A\cup B_i)-f(A\cup B_{i-1})\\ & ⩽f(A)+\sum _{i=1}^{n}f(B_i)-f(B_{i-1})\\ & =f(A)+f(B)\end{array}$$

上述不等式是因为 $f(A\cup B_{i-1}\cup e_i)-f(A\cup B_{i-1})⩽f(B_{i-1}\cup e_i)-f(B_{i-1})$
3⟹1: 考虑$S\subseteq T\subseteq N,e\in N\backslash T$记$T^{\prime }=T\backslash S$

$$\begin{array}{rl}{f}_T(e)& =f_S(T^{\prime }\cup e)-f_S(T^{\prime })\\ & ⩽f_S(T^{\prime })+f_S(e)-f_S(T^{\prime })=f_S(e)\end{array}$$

证毕。
接下来给出一个非常重要的引理

Corollary 1 设f是submodular函数，则

$$\forall S\subseteq T\subseteq N,f(T)⩽f(S)+\sum _{e\in T\backslash S}{f}_S(e)$$

如果f是monotone submodular 那么S不需要是T是子集

$$\forall S\subseteq N,\forall T\subseteq N,f(T)⩽f(S)+\sum _{e\in T\backslash S}{f}_S(e)$$

证明：如果f是submodular的，那么根据其subadditive性质：

$$f_S(T)=f_S(T\backslash S)⩽\sum _{e\in T\backslash S}{f}_S(e)$$

因为$f_S(T)=f(S\cup T)-f(S)$，若$S\subseteq T$显然有$f(S\cup T)=f(T)$,若$S̸\subseteq T$,根据monoton性质，有$f(T)⩽f(S\cup T)$，于是$f(T)-f(S)⩽f(S\cup T)-f(S)$,
证毕。

Cardinality constraint

现在我们第一个想要推的定理就是使用贪婪法得到的长度不超过K的子集与最优子集的差距最少也有$1-\frac{1}{e}$。不妨假设$f(\varphi )=0$，（如果不为0，可以减去一个常数让他为0），先来考虑一个最简单的约束条件，我们希望找到长度最多为K的最优子集，使用贪婪算法来搜索：
$$S^{\ast }=\arg \underset{S:|S|⩽K}{\max }f(S)$$

并使用如下贪婪算法去搜索：

可以证明上述算法$S_G$的近似程度为(1- 1/e)：

Theorem 1 $S_G$ achieves a (1- 1/e)-approximation of the optimum.
证明：
令$S_i=\{e_1,...,e_i\}$表示$S_G$是由贪婪算法在第i步返回的结果，且$S^{\ast }$为最优的集合。

$$\begin{array}{rl}f\left(S^{\ast }\right)& ⩽f(S_{i-1})+\sum _{e\in S^{\ast }\backslash S_{i-1}}{f}_{S_{i-1}}(e)\\ & =f(S_{i-1})+\sum _{e\in S^{\ast }\backslash S_{i-1}}f(S_{i-1}\cup e)-f(S_{i-1})\\ & ⩽f(S_{i-1})+\sum _{e\in S^{\ast }\backslash S_{i-1}}f(S_i)-f(S_{i-1})\\ & ⩽f(S_{i-1})+K(f(S_i)-f(S_{i-1}))\end{array}$$
第一个不等式来自与推论1。第二个不等式是因为在贪婪算法中，在第i步加入的e一定是最优的，即$f(S_i)⩾f(S_{i-1}\cup e)$，第三个不等于号是因为我们约束$|S|⩽K$，所以最多只有K个求和。
同时减去$Kf\left(S^{\ast }\right)$：
$$\begin{array}{rl}f(S_{i-1})+Kf(S_i)-Kf(S_{i-1})-Kf\left(S^{\ast }\right)& ⩾f\left(S^{\ast }\right)-Kf\left(S^{\ast }\right)\\ Kf(S_i)-Kf\left(S^{\ast }\right)& ⩾f\left(S^{\ast }\right)-Kf\left(S^{\ast }\right)+Kf(S_{i-1})-f(S_{i-1})\\ f(S_i)-f\left(S^{\ast }\right)& ⩾\frac{K-1}{K}\left(f(S_{i-1})-f\left(S^{\ast }\right)\right)\\ & ⩾{\left(\frac{K-1}{K}\right)}^2\left(f(S_{i-2})-f\left(S^{\ast }\right)\right)\\ & ...\end{array}$$

然后我们一直将$S_{i-1},S_{i-2},...$往下展开从而有

$$\begin{array}{rl}f(S_i)& ⩾\left(1-{\left(1-\frac{1}{K}\right)}^i\right)f\left(S^{\ast }\right)\end{array}$$

又因为$(1-\frac{1}{K}{)}^K\le \frac{1}{e}$，所以

$$\begin{array}{rl}f(S_i)& ⩾\left(1-\frac{1}{e}\right)f\left(S^{\ast }\right)\end{array}$$

证毕。

Knapsack Constraint

接来下介绍一下另一种约束，有时候，其集合长度不一定是固定的，每将一个元素加进集合都可能导致一些成本，所以，考虑在一定成本下，找到最优的集合就很重要。考虑成本函数$c:N\to R^{+}$和预算$B\in R^{+}$,考虑如下优化问题：
$$S^{\ast }\in \arg \underset{S:c(S)⩽B}{\max }f(S)$$

在这种约束下，有很多种不同的贪婪策略，不同的策略会有不同的界，一个最简单的策略就是从每次选择最大提升的元素加入S，变成每次选择性价比最高元素加入集合S。

Matroid Constraint

那么什么时候，贪婪算法可以得到最优解呢？ 答案是，如果我们在搜索子集的时候，搜索空间中所有的子集都是“独立”的，那么我们是有可能用贪婪算法找到最优解的。而Matriod定义了这么一种独立的性质.

想要进一步了解可以访问以下参考资料。

参考资料

When Greedy Algorithms are Good Enough: Submodularity and the (1 – 1/e)-Approximation
When Greedy Algorithms are Perfect: the Matroid
Notes on Greedy Algorithms for Submodular Maximization
Submodular Function Maximization