关于《连连看》的算法研究和演示Demo
连连看曾经是一款非常受欢迎的游戏，同时它也是一款比较古老的游戏。看到这里你千万不要认为本篇文章打算讨论《连连看》的历史以及它取得的丰功伟绩。恰恰相反，在这篇文章中我们打算讨论该游戏背后的实现思想，包括它定义的游戏规则，以及游戏的实现算法。作为应用，我们还将利用Java代码实现一个通用的《连连看》算法，并使用Java Swing框架创建一个演示实例。
1《连连看》的游戏规则是如何定义的？
连连看的游戏界面和游戏规则都非常简单。游戏界面可以简单看作一个具有M×N个单元格的棋盘，每个单元格内部显示着各种图片，游戏的最终目的是消除所有图片。但是在消除的过程中，我们需要遵守以下规则：
- 只有内容相同的图片才有消除的可能
- 每次只能消除两张图片，消除时需要使用鼠标指定（即连接）
- 两张图片连接时所经过的路径（连接路径）不能超过两个拐点
- 连接路径经过的单元格所包含的图片必须已经消除
直观感受，第一条和第二条规则不应该是算法完成的任务，因为这两条规则实现起来比较简单，应该尽量放在游戏逻辑中完成，避免算法与游戏逻辑产生强依赖关系。实现第三条和第四条规则有一个非常经典的算法理论，该算法就是接下来我们要讲的分类搜索算法。
2 分类搜索算法的原理
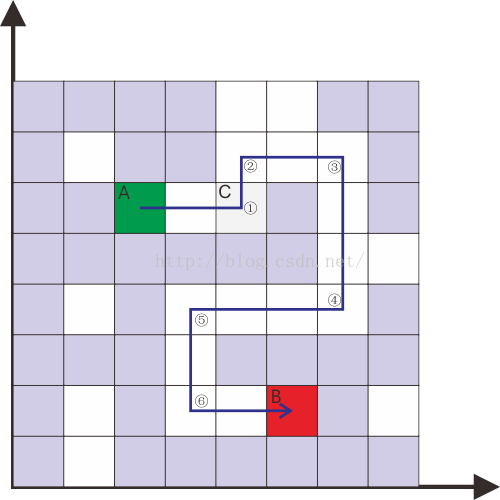
分类搜索算法的基本原理是一种递归思想。假设我们要判断A单元与B单元格是否可以通过一条具有N个拐点的路径相连，该问题可以转化为能否找到一个C单元格，C与A可以直线连接（0折连接），且C与B可以通过一条具有N-1个拐点的路径连接。下面截图解释了这一思想。图中，白色和浅灰色的单元格表示没有内容，可以连通。可以发现，A与B连接必须经过①②③④⑤⑥个拐点。假设我们找到了一个可以直接与A连接的C点，那么只需要搜索C与B连接需要经过的②③④⑤⑥个拐点即可。
基于连连看要求的拐点数不能超过2个的规则，我们可以将上述思想简化为三种情况。
1）0折连接
0折连接表示A与B的X坐标或Y坐标相等，可以直线连接，不需要任何拐点，且连通的路径上没有任何阻碍，具体可以分为下面两种情况。
2）1折连接
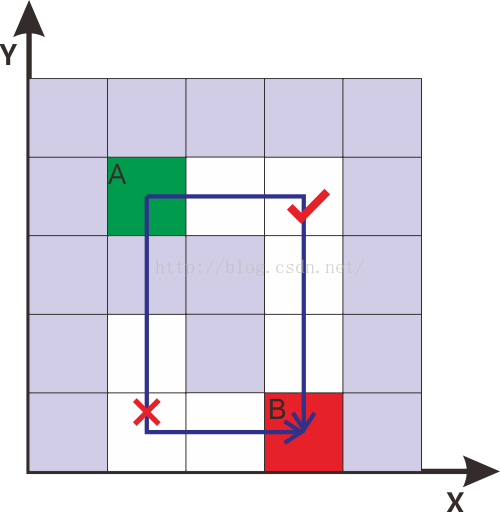
1折连接与0折连接恰好相反，要求A单元格与B单元格的X轴坐标与Y轴坐标都不能相等。此时通过A与B可以画出一个矩形，而A与B位于矩形的对角点上。判断A与B能否一折连接只需要判断矩形的另外两个对角点是否有一个能同时与A和B满足0折连接。下面截图说明了1折连通的原理：
3）2折连接
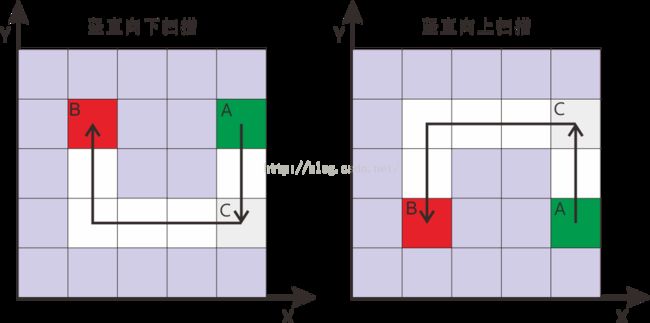
根据递归的思想，判断A单元格与B单元格能否经过两个拐点连接，可以转化为判断能否找到一个C单元格，该C单元格可以与A单元格0折连接，且C与B可以1折连接。若能找到这样一个C单元格，那么A与B就可以2折连接，下面截图解释了2折连接的情况：
判断A单元格和B单元格是否可以2折连接时需要完成水平和竖直方向上的扫描。观察下面两幅截图，A与B单元格的连接属于典型的2折连接，首先我们需要找到图中的C单元格，然后判断C与B单元格是否可以1折连接。在搜索C单元格时我们必须从A单元格开始，分别向右、向左扫描，寻找同时可以满足与A单元格0折连接，与B单元格1折连接的C单元格。
同样，如果A与B单元格的位置关系是下面两幅截图展示的那样。那么我们就需要在垂直方向完成向上、向下搜索，找到符合要求的C单元格。
上面我们讨论了分类搜索法的实现原理，接下来我们使用Java语言实现一个通用的分类搜索算法。
3 如何实现通用的分类搜索算法
前面多次强调，我们需要实现一个通用的分类搜索算法。通用意味着算法与具体的实现分离。上面介绍的分类搜索算法建立在一个二维数组的前提下，但是我们应该使用何种类型的二维数组呢？为了满足上述要求，我们应该定义一个所有希望使用该算法的应用都应该实现的一个接口，然后在算法中使用该接口类型的二维数组。
那么该接口应该包含些什么方法呢？根据上面对算法的分析，分类搜索算法唯一需要判断的就是每个单元格的连通性，即单元格是否已经填充。理解了这些内容，下面我们创建该接口。
public interface LinkInterface {
public boolean isEmpty();
public void setEmpty();
public void setNonEmpty();
}
上面我们将该接口起名为LinkInterface，并且声明了三个方法，分别用于设置或判断单元格的连通性。
为了保证算法的独立性，我们还应该创建一个用于表示单元格位置的Point类：
public class Point {
public int x;
public int y;
public Point(){}
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
1）0折连通算法
接下来我们来实现0折连通的算法。首先我们需要声明一个类，这里我们将该类声明为LinkSerach。下面我们需要思考0折连通需要些什么参数，以及返回值应该是什么？首先，我们必须传递一个实现了LinkInterface接口的类的数组对象。其次我们还必须传递A和B的位置坐标。搜索算法的一个重要功能就是返回搜索的路径。对于0折连接，即使搜索到可用路径，我们也不用返回任何路径，因为整个连通路径就是A和B点的连线。但是我们必须返回一个可以表明搜索是否成功的boolean类型值。接下来创建该方法：
public class LinkSearch {
private static boolean MatchBolck(LinkInterface[][] datas,
final Point srcPt, final Point destPt) {
// 如果不属于0折连接则返回false
if(srcPt.x != destPt.x && srcPt.y != destPt.y)
return false;
int min, max;
// 如果两点的x坐标相等，则在水平方向上扫描
if(srcPt.x == destPt.x) {
min = srcPt.y < destPt.y ? srcPt.y : destPt.y;
max = srcPt.y > destPt.y ? srcPt.y : destPt.y;
for(min++; min < max; min++) {
if(!datas[srcPt.x][min].isEmpty())
return false;
}
}
// 如果两点的y坐标相等，则在竖直方向上扫描
else {
min = srcPt.x < destPt.x ? srcPt.x : destPt.x;
max = srcPt.x > destPt.x ? srcPt.x : destPt.x;
for(min++; min < max; min++) {
if(!datas[min][srcPt.y].isEmpty())
return false;
}
}
return true;
}
}
0折连通算法的核心思想是根据A、B单元格的相对位置将扫描过程分解为水平和竖直两个方向。
2）1折连接
1折连接算法与0折连接算法输入参数相同，但是1折连接算法应该返回搜索路径。那么应该如何处理呢？由于1折连接算法最多只有1个拐点，而整个路径就是两个搜索单元格的位置加上该拐点的位置，需要搜索的单元格位置用户已经知道，因此我们只需要返回拐点的位置即可，当没有搜索到连接路径时可以返回null值，下面是1折连接的搜索算法：
private static Point MatchBolckOne(LinkInterface[][] datas,
final Point srcPt, final Point destPt) {
// 如果不属于1折连接则返回null
if(srcPt.x == destPt.x || srcPt.y == destPt.y)
return null;
// 测试对角点1
Point pt = new Point(srcPt.x,destPt.y);
if(datas[pt.x][pt.y].isEmpty()) {
boolean stMatch = MatchBolck(datas, srcPt, pt);
boolean tdMatch = stMatch ?
MatchBolck(datas, pt, destPt) : stMatch;
if (stMatch && tdMatch) {
return pt;
}
}
// 测试对角点2
pt = new Point(destPt.x, srcPt.y);
if(datas[pt.x][pt.y].isEmpty()) {
boolean stMatch = MatchBolck(datas, srcPt, pt);
boolean tdMatch = stMatch ?
MatchBolck(datas, pt, destPt) : stMatch;
if (stMatch && tdMatch) {
return pt;
}
}
return null;
}
3)2折连接
可以发现，0折算法和1折算法都是独立，如果是1折连接的情况，我们是不能使用0折算法进行判断的，同样，属于0折的情况，我们也是不能使用1折算法进行判断的。为了建立一种通用的方法，我们必须在2折连接算法里包含上述两种算法的判断,这也是为什么我们将上述两个方法声明为private的原因，因为我们只需要为用户暴露2折算法的方法即可。还有，2折连接需要返回一个包含两个拐点的路径，此处我们使用Java基础库的LinkedList来实现，具体代码如下：
public static List MatchBolckTwo(LinkInterface[][] datas,
final Point srcPt, final Point destPt) {
if(datas == null || datas.length == 0)
return null;
if(srcPt.x < 0 || srcPt.x > datas.length)
return null;
if(srcPt.y < 0 || srcPt.y > datas[0].length)
return null;
if(destPt.x < 0 || destPt.x > datas.length)
return null;
if(destPt.y < 0 || destPt.y > datas[0].length)
return null;
// 判断0折连接
if(MatchBolck(datas, srcPt, destPt)) {
return new LinkedList<>();
}
List list = new LinkedList();
Point point;
// 判断1折连接
if((point = MatchBolckOne(datas, srcPt, destPt)) != null) {
list.add(point);
return list;
}
// 判断2折连接
int i;
for(i = srcPt.y + 1; i < datas[srcPt.x].length; i++) {
if(datas[srcPt.x][i].isEmpty()) {
Point src = new Point(srcPt.x, i);
Point dest = MatchBolckOne(datas, src, destPt);
if(dest != null) {
list.add(src);
list.add(dest);
return list;
}
} else break;
}
for(i = srcPt.y - 1; i > -1; i--) {
if(datas[srcPt.x][i].isEmpty()) {
Point src = new Point(srcPt.x, i);
Point dest = MatchBolckOne(datas, src, destPt);
if(dest != null) {
list.add(src);
list.add(dest);
return list;
}
} else break;
}
for(i = srcPt.x + 1; i < datas.length; i++) {
if(datas[i][srcPt.y].isEmpty()) {
Point src = new Point(i, srcPt.y);
Point dest = MatchBolckOne(datas, src, destPt);
if(dest != null) {
list.add(src);
list.add(dest);
return list;
}
} else break;
}
for(i = srcPt.x - 1; i > -1; i--) {
if(datas[i][srcPt.y].isEmpty()) {
Point src = new Point(i, srcPt.y);
Point dest = MatchBolckOne(datas, src, destPt);
if(dest != null) {
list.add(src);
list.add(dest);
return list;
}
} else break;
}
return null;
}
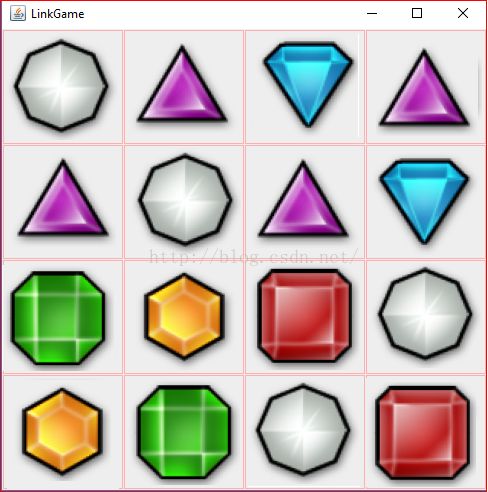
4 接下来我们利用Java Swing框架创建一个演示实例
除了上面创建的两个类之外，我们还需要创建一个表示每个单元格的LinkItem类，以及一个创建框架的主类LinkGame。创建类之前，我们还需寻找一些示例图片。这里我们使用GitHub上的一个开源项目freegemas的资源图片，下面截图显示了我们的即将使用的七张图片资源：
创建LinkItem类：
public class LinkItem extends JComponent implements LinkInterface {
private static LinkItem selectedItem;
private static LinkItem targetItem;
private int rowId = -1;
private int colId = -1;
private boolean empty = true;
private Image image;
private Stroke defaultStroke;
public LinkItem() {
setLayout(new FlowLayout());
defaultStroke = new BasicStroke(2, BasicStroke.CAP_BUTT,
BasicStroke.JOIN_ROUND, 1f);
}
@Override
protected void paintComponent(Graphics g) {
Graphics2D g2 = (Graphics2D)g;
int width = getWidth();
int height = getHeight();
// 激活时才填充并显示内容
if(!empty && image != null) {
g2.drawImage(image.getScaledInstance(width - 8, height - 8,
Image.SCALE_SMOOTH), 4, 4, null);
}
// 绘制边框的颜色
if(selectedItem == this) {
g2.setColor(Color.RED);
g2.setStroke(defaultStroke);
}
else if(targetItem == this) {
g2.setColor(Color.ORANGE);
g2.setStroke(defaultStroke);
} else {
g2.setColor(Color.PINK);
}
g2.drawRect(1, 1, width - 2, height - 2);
}
public static LinkItem getSelectedItem() {
return selectedItem;
}
public static void setSelectedItem(LinkItem selectedComponent) {
LinkItem.selectedItem = selectedComponent;
}
public static LinkItem getTargetItem() {
return targetItem;
}
public static void setTargetItem(LinkItem targetComponent) {
LinkItem.targetItem = targetComponent;
}
@Override
public boolean equals(Object obj) {
if(!(obj instanceof LinkItem))return false;
else {
LinkItem item = (LinkItem)obj;
if(image == null || item.getImage() == null)
return false;
return (this.image == item.image);
}
}
public void setRow(int row) {
this.rowId = row;
}
public void setCol(int col) {
this.colId = col;
}
public int getRow() {
return rowId;
}
public int getCol() {
return colId;
}
public Image getImage() {
return image;
}
public void setImage(Image image) {
this.image = image;
}
@Override
public boolean isEmpty() {
return empty;
}
@Override
public void setEmpty() {
empty = true;
}
@Override
public void setNonEmpty() {
empty = false;
}
}
上述代码很简单，如果你对Java Swing不是很了解，那先去看看《Java核心编程》第一卷的第七和第八章。需要解释的一点是，selectedItem和targetItem都是静态成员变量，用于保存当前选中的对象以及需要配对的目标对象，即A和B单元格。image.getScaledInstance(,,Image.SCALE_SMOOTH)调用非常重要，如果你直接使用g2.drawImage()方法绘制图片的话，最终界面看起来将非常糟糕，不信你可以试试，这是由于图片锯齿化造成的，而getScaledInstance方法配合SCALE_SMOOTH参数可以返回抗锯齿的图片对象。还有，该类继承于JCompont是为了利用Java Swing的GridLayout布局管理器将整个棋盘排列起来。在构造器中必须调用setLayout(new FlowLayout())代码，如果不调用，Item将不会显示。
创建主类LinkGame：
public class LinkGame {
public static void main(String[] args) {
EventQueue.invokeLater(new Runnable() {
@Override
public void run() {
// 创建并启动框架
JFrame frame = new LinkFrame();
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
frame.setVisible(true);
}
});
}
}
class LinkFrame extends JFrame {
private static final long serialVersionUID = 1L;
private static final int DEFAULT_WIDTH = 500;
private static final int DEFAULT_HEIGHT = 500;
// 棋盘格数 (rows * cols) % 2必须等于0
private static final int rows = 8;
private static final int cols = 8;
// 所有单元格
private final LinkItem[][] items;
// 棋子可以选的显示内容图片
private static Image[] optImgs;
private static int optCount = 7;
// 选中对象的位置
private int selRow = -1;
private int selCol = -1;
// 是否已经选中一个对象
private boolean isSelected;
// 结果路径
private List pathList;
// 窗口边框和标题栏的尺寸
private Insets insets;
// 绘制路径时使用的默认线性
private Stroke defaultStroke;
public LinkFrame() {
setTitle("LinkGame");
// 设置为网格布局管理器
setSize(DEFAULT_WIDTH, DEFAULT_HEIGHT);
setLayout(new GridLayout(rows, cols));
defaultStroke = new
BasicStroke(5, BasicStroke.CAP_ROUND,
BasicStroke.JOIN_BEVEL, 1f);
// 初始没有选中对象
isSelected = false;
// 为Item创建鼠标事件处理器
MouseHandler handler = new MouseHandler();
// 加载图片
optImgs = new Image[optCount];
for(int i = 0; i < optImgs.length; i++) {
String path = "assets/images/"+ (i + 1) + ".png";
File file;
try {
file = new File(path);
optImgs[i] = ImageIO.read(file);
} catch (IOException e) {
e.printStackTrace();
}
}
// 创建棋盘并初始化
items = new LinkItem[rows][cols];
LinkItem comp;
for(int i = 0; i < items.length; i++) {
for(int j = 0; j < items[i].length; j++) {
comp = items[i][j] = new LinkItem();
comp.addMouseListener(handler);
comp.setImage(optImgs[(int)(Math.random() * optImgs.length)]);
comp.setNonEmpty();
comp.setRow(i);
comp.setCol(j);
add(comp);
}
}
}
@Override
public void paint(Graphics g) {
super.paint(g);
Graphics2D g2 = (Graphics2D)g;
// 抗锯齿
g2.setRenderingHint(RenderingHints.KEY_ANTIALIASING,
RenderingHints.VALUE_ANTIALIAS_ON);
// 更新窗口边框尺寸
insets = getInsets();
// 设置线性和颜色
g2.setStroke(defaultStroke);
g2.setColor(Color.CYAN);
// 如果存在路径则绘制
if(pathList != null) {
Point pre = pathList.get(0); // 前一点
for(int i = 1; i < pathList.size(); i++) {
Point next = pathList.get(i); // 下一点
// 获得两点对应的对象
LinkItem a = items[pre.x][pre.y];
LinkItem b = items[next.x][next.y];
int x1 = insets.left + a.getX() + a.getWidth() / 2;
int x2 = insets.left + b.getX() + b.getWidth() / 2;
int y1 = insets.top + a.getY() + a.getHeight() / 2;
int y2 = insets.top + b.getY() + b.getHeight() / 2;
g2.drawLine(x1, y1, x2, y2);
// 在最后一个点处填充一个圆
if(i == pathList.size() - 1) {
g2.draw(new Ellipse2D.Float(x2 - 2, y2 - 2, 4, 4));
}
pre = next;
}
}
}
private class MouseHandler extends MouseAdapter {
@Override
public void mouseReleased(MouseEvent e) {
LinkItem curComp = (LinkItem) e.getSource();
// 刷新边框
curComp.repaint();
if(!isSelected) {
// 设置选中对象并取消目标对象
LinkItem.setSelectedItem(curComp);
LinkItem.setTargetItem(null);
selRow = curComp.getRow();
selCol = curComp.getCol();
} else {
// 设置目标对象并取消选中对象
LinkItem.setSelectedItem(null);
LinkItem.setTargetItem(curComp);
// 判断是否可以连接
LinkItem srcComp = items[selRow][selCol];
if(curComp.equals(srcComp) && curComp != srcComp
&& !curComp.isEmpty() && !srcComp.isEmpty()) {
Point srcPt = new Point(selRow, selCol);
Point destPt = new Point(curComp.getRow(), curComp.getCol());
// 搜索路径
pathList = LinkSearch.MatchBolckTwo(items, srcPt, destPt);
// 如果存在链接路径则消除单元格内容
// 并为搜索路径添加起止单元格
if(pathList != null) {
srcComp.setEmpty();
curComp.setEmpty();
srcComp.repaint();
curComp.repaint();
pathList.add(0, srcPt);
pathList.add(destPt);
LinkFrame.this.repaint();
}
}
}
// 转换选中状态
isSelected = !isSelected;
}
}
}
运行游戏
接下来运行游戏，最终结果如下图所示：
下面是运行动画：
5 上述代码的缺陷
可能你还没有发现，上述代码具有致命缺陷。我们在初始化棋盘的时候是这样做的：
// 创建棋盘并初始化
items = new LinkItem[rows][cols];
LinkItem comp;
for(int i = 0; i < items.length; i++) {
for(int j = 0; j < items[i].length; j++) {
comp = items[i][j] = new LinkItem();
comp.addMouseListener(handler);
comp.setImage(optImgs[(int)(Math.random() * optImgs.length)]);
comp.setNonEmpty();
comp.setRow(i);
comp.setCol(j);
add(comp);
}
}
上述情况违反了连连看要求的必须将所有单元格消除的基本规则。
其实上述问题很容解决的。我们只需要保证每次为两个单元格设置同一个图片对象即可。深入思考一下，该任务应该属于算法的份内责任，所以我们应该将初始化棋盘的任务交给算法类处理。算法的初始化方法在填充棋盘时，至少应该知道填充的内容的类型吧！但是为了避免算法与实现产生强依赖，我们应该使用一种通用的类型表示填充对象的类型，这里可以使用Java的Object类，但是有一个更好的方法，那就是泛型编程。下面我们来改造上述算法，添加初始化方法。
首先修改LinkInterface接口，修改完成后的代码如下：
public interface LinkInterface {
public boolean isEmpty();
public void setEmpty();
public void setNonEmpty();
public T getContent();
public void setContent(T content);
}
接下来修改LinkItem类：
public class LinkItem extends JComponent implements LinkInterface {
private boolean empty = true;
private Image image;
...
@Override
public boolean isEmpty() {
return empty;
}
@Override
public void setEmpty() {
empty = true;
}
@Override
public void setNonEmpty() {
empty = false;
}
@Override
public Image getContent() {
return image;
}
@Override
public void setContent(Image content) {
this.image = content;
}
}
接下来按照下面代码修改LinkSearch算法类：
public class LinkSearch {
private static boolean MatchBolck(LinkInterface[][] datas,
final Point srcPt, final Point destPt) {
...
}
private static Point MatchBolckOne(LinkInterface[][] datas,
final Point srcPt, final Point destPt) {
...
}
public static List MatchBolckTwo(LinkInterface[][] datas,
final Point srcPt, final Point destPt) {
...
}
public static void generateBoard(LinkInterface[][] datas, T[] optConts) {
List list = new LinkedList<>();
for(int i = 0; i < datas.length; i++) {
for(int j = 0; j < datas[i].length; j++) {
list.add(new Point(i, j));
}
}
while (list.size() != 0) {
Point srcPt = list.remove((int)(Math.random() * list.size()));
Point destPt = list.remove((int)(Math.random() * list.size()));
LinkInterface src = datas[srcPt.x][srcPt.y];
LinkInterface dest = datas[destPt.x][destPt.y];
src.setNonEmpty();
dest.setNonEmpty();
T t = optConts[(int)(Math.random() * optConts.length)];
src.setContent(t);
dest.setContent(t);
}
}
}
首先 我们需要为前面实现的三个方添加泛型参数，接着创建一个generateBoard()方法，该方法需要一个LinkInterface类型的二维数组参数，该参数表示即将填充的棋盘，还有，我们需要传递一个T[]类型的数组对象，该数组包含了棋盘可以填充的所有选择。在方法内部，我们首先使用所有位置创建了一个列表，然后通过循环，每次从列表中随机删除并返回两个位置，然后对返回的这两个位置上的单元格填充相同的内容，并设置为非空，当列表中的所有元素被删除完之后跳出循环，结束初始化。
最后修改LinkFrame类的初始化代码，最终结果如下：
// 创建棋盘并初始化
items = new LinkItem[rows][cols];
LinkItem comp;
for(int i = 0; i < items.length; i++) {
for(int j = 0; j < items[i].length; j++) {
comp = items[i][j] = new LinkItem();
comp.addMouseListener(handler);
comp.setRow(i);
comp.setCol(j);
add(comp);
}
}
LinkSearch.generateBoard(items, optImgs);
}
从上面截图可以看到，每种图形都是偶数个，无论游戏进行到何时，都能保证总是存在可以连接的对象。上述规则就一定能将所有图片消除吗？如果出现下面情况，该怎么办？
其实解决上面问题有许多种方法，比如说使用拉斯维加斯算法和回溯法创建有效棋盘。该方法的基本思想是，随机选取两个位置判断是否可以连通，如果可以则继续从剩余的单元格随机选取两点，再进行判断。当判断两个单元格不能连通时，回溯到上一次随机选取的状态之前，重新尝试。该算法的优点是总能找到有效的棋盘。但是，该算法有一个致命的缺点，就是效率低，因此大多数时候我们都不应该使用该算法产生棋盘。
还有一种解决上述问题的方法是，将整个棋盘看作是一个以中心点为圆心的靶子，半径就是棋盘的一半宽度，然后从内到外或从外到内，逐步填充每环所经过的单元格。该方法
效率较高，但容易产生具有规则的棋盘。
很多游戏在解决上述问题都使用了模板的方法，即在游戏中保存几百或数千种游戏棋盘排列方式，然后再游戏中随机选取，随机填充不同类型的图片。
从概率的角度讲，实现一种生成有效棋盘的算法没有多大意义，因为即使产生的棋盘有效，我们在游戏时，最后也有可能将游戏的棋盘玩死。比如下面两幅截图：
本来整个棋盘是可以完全消除所有单元格的，但是由于我们操作的顺序发生了变化，最终导致棋盘无解。
还有，我们上面提到的一开始就无解的情况随着棋盘格子数的递增，出现的概率将越来越小，这一问题可以通过在生成棋盘时至少创建一对位置相邻的单元格来解决。
6 结束语
上面我们介绍了连连看的路径搜索算法和产生游戏棋盘的算法。如果从算法的角度思考的话，上面内容还有许多不足的地方，例如优化搜索算法、创建有效的棋盘。关于搜索算法还有很多种，由于篇幅有限，本文将不再介绍。
最后再提出两个未完成的问题，关于上面介绍的搜素算法我们是否可以扩展到N个拐点的递归算法呢？还有生成有效棋盘的拉斯维加斯算法和回溯法应该如何实现？如果你有更好的见解，请不吝赐教。