【小波变换】小波变换入门----haar小波
小波可以认为是一个带通滤波器,只允许频率和小波基函数频率相近的信号通过。小波变换的基本思想是用一组小波函数和基函数表示一个函数或者信号。
haar小波变换
首先,以haar小波变换过程为例来理解小波变换。
例:求只有4个像素[9 7 3 5]的图像的哈尔小波变换系数。 计算步骤如下:
步骤1:求均值(averaging),也叫Approximation。计算相邻像素对的平均值,得到一幅分辨率比较低的新图像,新的图像的分辨率是原来的1/2,相应的像素值为:[8 4]
步骤2:求差值(differencing)。很明显,用2个像素表示这幅图像时,图像的信息已经部分丢失。为了能够从由2个像素组成的图像重构出由4个像素组成的原始图像,就需要存储一些图像的细节系数(detail coefficient),以便在重构时找回丢失的信息。方法是使用这个像素对的差值除以2,结果为[8 4 1 -1]
步骤3:重复第1,2步,把由第一步分解得到的图像进一步分解成分辨率更低的图像和细节系数。[6 2 1 -1]
从这个例子中我们可以看到:
① 对这个给定的变换,我们可以从所记录的数据中重构出各种分辨率的图像。例如,在分辨率为1的图像基础上重构出分辨率为2的图像,在分辨率为2的图像基础上重构出分辨率为4的图像。
②变换过程中没有丢失信息,因为能够从所记录的数据中重构出原始图像。
③ 通过变换之后产生的细节系数的幅度值比较小,这就为图像压缩提供了一种途径,例如去掉一些微不足道的细节系数并不影响对重构图像的理解。
一维离散小波变换
经过小波变换后图像会生成低频信息和高频信息。低频信息对应于求均值,高频信息对应于求差值。
均值是局部的平均值,变化缓慢,属于低频信息,存储图片的轮廓信息,近似信息
差值是局部的波动值,变化较快,属于高频信息,存储图片的细节信息,局部信息,另外含有噪音
h h i g h h_{high} hhigh是高通滤波器,允许高频信息通过
h h i g h h_{high} hhigh是低通滤波器,允许低频信息通过
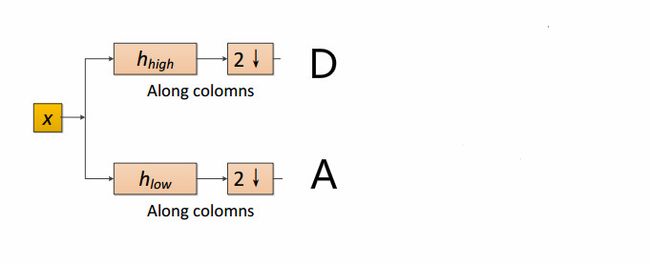
在haar小波中, h h i g h = ( 1 2 , − 1 2 ) h_{high}=(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}}) hhigh=(21,−21), h l o w = ( 1 2 , 1 2 ) h_{low}=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}) hlow=(21,21)
import pywt
data = [1, 1, 1, 1]
coeffs = pywt.dwt(data, 'haar')
# (cA, cD) : tuple Approximation and detail coefficients.
cA, cD = coeffs
cA:[1.41421356 1.41421356]
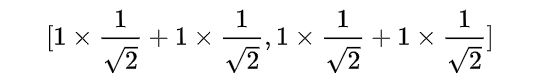
cD:[0. 0.]
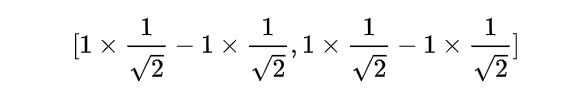
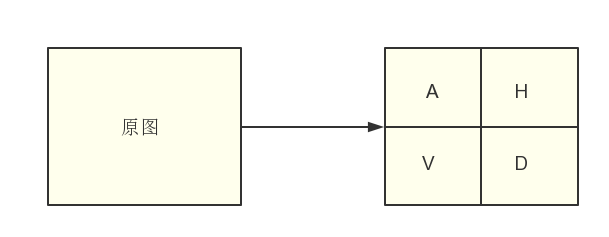
二维离散小波变换
h h i g h h_{high} hhigh是高通滤波器,允许高频信息通过
h h i g h h_{high} hhigh是低通滤波器,允许低频信息通过

A是低频信息,H是水平高频信息,V是垂直高频信息、D是对角高频信息。
import numpy as np
import pywt
data = np.ones((4, 4), dtype=np.float64)
[[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
coeffs = pywt.dwt2(data, 'haar')
# (cA, (cH, cV, cD)) : tuple
# Approximation, horizontal detail, vertical detail and diagonal
# detail coefficients respectively
cA, (cH, cV, cD) = coeffs
print(cA)
[[2. 2.]
[2. 2.]]
print(cH)
[[0. 0.]
[0. 0.]]
假设一张图片只有4个像素,其经过2-D DWT之后得到4张子图,每个子图的详细计算过程如下:
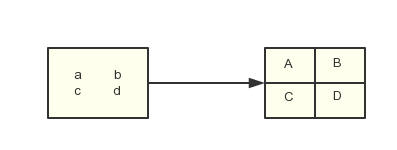
A = 1 2 ( a + b + c + d ) A=\frac{1}{2}(a+b+c+d) A=21(a+b+c+d)
B = 1 2 ( a − b + c − d ) B=\frac{1}{2}(a-b+c-d) B=21(a−b+c−d)
C = 1 2 ( a + b − c − d ) C=\frac{1}{2}(a+b-c-d) C=21(a+b−c−d)
D = 1 2 ( a − b − c + d ) D=\frac{1}{2}(a-b-c+d) D=21(a−b−c+d)
更多相关资料:
小波变换入门参考资料
[Python ]小波变化库——Pywalvets