Matlab计算最短路径及路径的个数
最近老板让计算最短路径及路径个数,找遍了所有工具箱,都没现成的。急死了,什么Dijkstra和Floyd都搞不定。最后,想了想,算了吧,自己编吧,反正自己用,又没有算法复杂度要求。于是自己就写了个小程序(本程序仅限无权无向连通图),算法复杂度不晓得()。
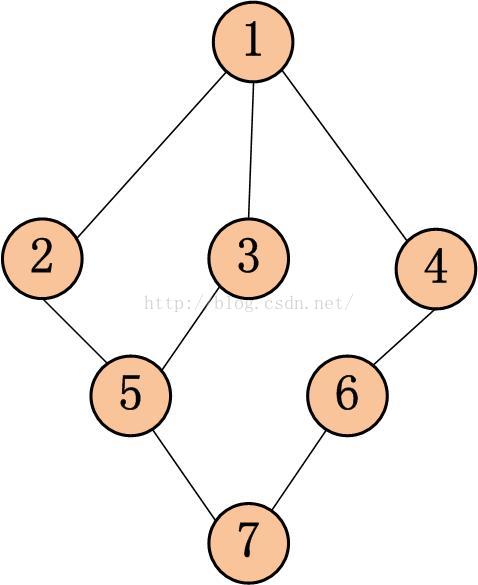
本人不是计算机出身,就不写算法步骤了,直接上图解。
我们首先计算的是节点1到所有节点的最短路径,及个数。s存放节点1到所有节点的最短路径,p_num存放路径的个数。
初始化:s=[0,0,0,0,0,0,0] p_num=[1,0,0,0,0,0,0]
第一轮迭代:找节点1的所有邻居节点2,3,4。则:s([2,3,4])=1
在看节点2的邻居1和5.则: p_num(2)= p_num(1)+ p_num(5)=1+0=1
同理:p_num(3)=p_num(4)=1
则本轮会得到:s=[0,1,1,1,0,0,0] p_num=[1,1,1,1,0,0,0]
第二轮迭代:找节点2,3,4的所有邻居节点(没有被找过的节点)5,6。则:s([5,6])=2
再看节点5的邻居2,3和7.则: p_num(5)= p_num(2)+ p_num(3)+ p_num(7)=1+1+0=2
同理:p_num(6)=1
则本轮会得到:s=[0,1,1,1,2,2,0] p_num=[1,1,1,1,2,1,0]
第三轮迭代:找节点5,6的所有邻居节点(没有被找过的节点)7。则:s([7])=3
在看节点7的邻居5和6.则: p_num(2)= p_num(5)+ p_num(6)=2+1=3
则本轮会得到:s=[0,1,1,1,2,2,3] p_num=[1,1,1,1,2,1,3]
找节点7的所有邻居节点(没有被找过的节点),没啦,迭代终止。哈哈节点到所有节点的最短路径及条数搞定,然后来个循环就把任意两个点的最短路径及个数搞定。
哇嘎嘎,简单粗暴,下面有程序,能力有限。使用前记得要仔细拍错误哦哦
%全联通无权无向图
%输入邻接矩阵w
%all_s为所有节点间的最短距离
%all_p_num为最短路径的个数
%树状搜索(纯属自己想的,没有优化,可以跑小网络)
n=length(w); %节点的个数
all_s=zeros(n,n); %初始化
all_p_num=zeros(n,n); %初始化
for i=1:n
[s,p_num]=node_shortest(w,i);
all_s(i,:)=s;
all_p_num(i,:)=p_num;
end
end
function [s,p_num]=node_shortest(w,node)
%全联通无权无向图
%输入邻接矩阵w
%初始节点 node
%s为node到所有节点的最短距离
%p_num为最短路径的个数
%树状搜索(纯属自己想的)
n=length(w); %节点的个数
s=zeros(1,n); %初始化
p_num=zeros(1,n); %初始化
p_num(node)=1; %node到node本身距离为零,个数记为1
node_all=zeros(1,n);
node_all(node)=1; %记录哪些节点被搜索到,搜索到的节点记为1,否则为0
lj=node; %lj为当前步到达的节点(到lj的距离都为k)
k=1;
while sum(node_all)
s(lj)=k; %记录时刻即路径长度
p_num(lj)=sum(w(:,lj).*repmat(p_num',[1,length(lj)]),1); %这一时刻的路径的条数为:这个节点上一时刻已经到达的邻居的所有路径和
node_all(lj)=1; %这些节点在这个时刻已经被找到
k=k+1; %下一时刻
end
end