时间序列 R 08 指数平滑 Exponential smoothing

1.1 简单指数平滑

“simple exponential smoothing” (SES)
SES适用于不计趋势与季节性的时间序列
我们在可以使用平均值模型和naive模型来做粗略的预测（点击查看），他们懂预测方法分别是
- 使用最后一个值（naive模型）
- 使用前面值的平均数（平均值）
这里的简单指数平滑是用的前面几个值的加权平均数，越靠近最后的权重越大，后面的权重指数下降
SES的公式如下

y^T+1|T=αyT+α(1−α)yT−1+α(1−α)2yT−2+⋯

α 就是平滑指数，值越大越忽略距离远的数值。
还可以写成以下形式：、

y^t+1|t=αyt+(1−α)y^t|t−1

其中第一个的值的计算公式如下：

y^2|1=αy1+(1−α)ℓ0

我们可以发现这样的问题：其中的 ℓ0 与 α 的值怎么选取最好？
通常的简单做法直接把 ℓ0 设置为y0。
这里我们可以借鉴最小二乘法的方法，通过求解SSE（sum of the squared errors）求最佳参数。
下图显示了不同参数时的SSE值，其中最后一个是通过求解SSE最小值得到的


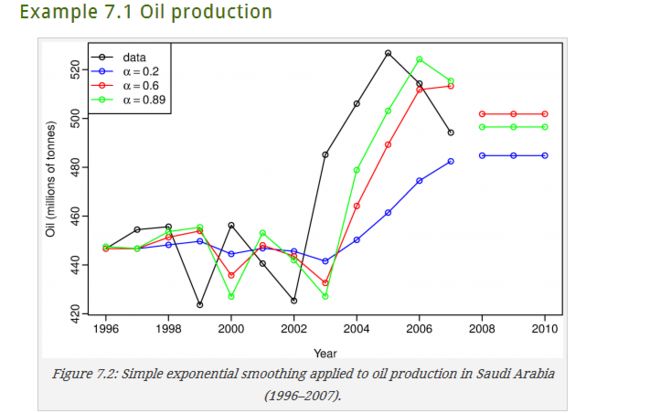
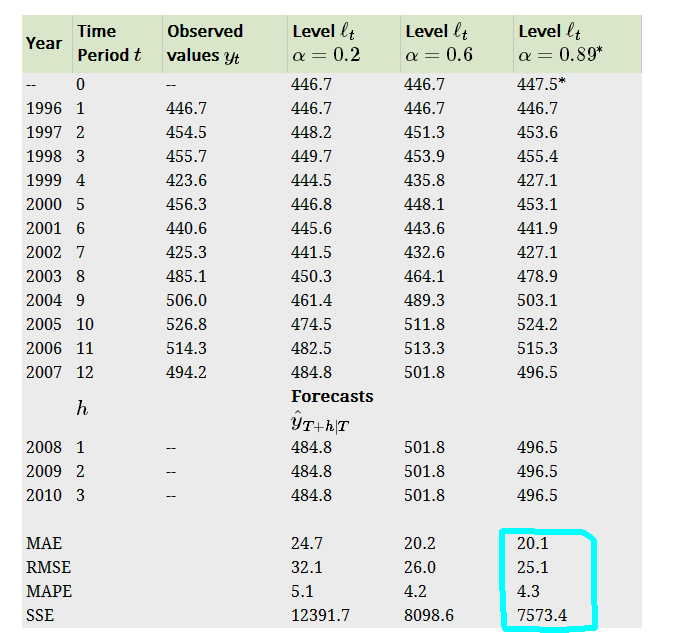
由此可以看出简单指数平滑初步的可以选择了拟合较好的值来预测，比起最初的简单模型要更加合理

1.2 霍尔特线性趋势预测 Holt’s linear trend method

前面的简单指数平滑只能预测一个相同的值，不能有趋势，可以进行一定的线性预测，Holt将其进行了改进，加入了二次平滑，其公式如下：

Forecast equationLevel equationTrend equationyt+h|tℓtbt=ℓt+hbt=αyt+(1−α)(ℓt−1+bt−1)=β∗(ℓt−ℓt−1)+(1−β∗)bt−1

其中b是斜率，其中包含的迭代公式就是第二次平滑。
同样其参数的确定可以根据SSE来计算
sse公式

ℓtbt=ℓt−1+bt−1+αet=bt−1+αβ∗et

et=yt−(ℓt−1+bt−1)=yt−yt|t−1

如果其预测值可以有限性趋势，图中其他方法将在后续介绍

1.3 指数趋势预测法Exponential trend method

该方法是将线性趋势中的斜率又一个加数变为了一个乘数因子，公式如下：

yt+h|tℓtbt=ℓtbht=αyt+(1−α)(ℓt−1bt−1)=β∗ℓtℓt−1+(1−β∗)bt−1

误差公式为：

ℓtbt=ℓt−1bt−1+αet=bt−1+αβ∗etℓt−1

et=yt−(ℓt−1bt−1)=yt−yt|t−1

1.4 衰减趋势法 Damped trend methods

前面两种方法都会使其预测值随着时间的增长越来越大，或者越来越小，显然如果时间很长，预测值可能不合适，damped trend methods 就是一种将趋势在增加到一定程度就不增加的方法。

1.4.1 Additive damped trend加法模式:

公式如下：

yt+h|tℓtbt=ℓt+(ϕ+ϕ2+⋯+ϕh)bt=αyt+(1−α)(ℓt−1+ϕbt−1)=β∗(ℓt−ℓt−1)+(1−β∗)ϕbt−1.

上式中如果 ϕ=1 那么就是holt线性趋势预测，如果其值在（0,1）上，上式是一个收敛的级数，h->无穷时，其值接近于常数
误差公式：

ℓtbt=ℓt−1+ϕbt−1+αet=ϕbt−1+αβ∗et.

1.4.2 Multiplicative damped trend 乘法模式

yt+h|tℓtbt=ℓtb(ϕ+ϕ2+⋯+ϕh)t=αyt+(1−α)ℓt−1bϕt−1=β∗ℓtℓt−1+(1−β∗)bϕt−1.

误差公式：

ℓtbt=ℓt−1bϕt−1+αet=bϕt−1+αβ∗etℓt−1.

1.4.3 示例

上面两种方法的参数都可以通过最小二乘法求出
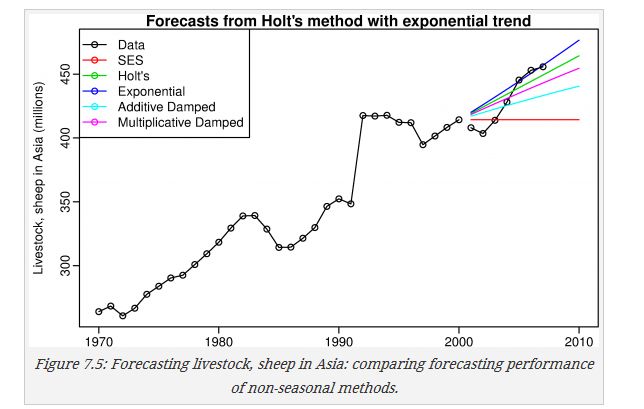
下面是几种方法的比较;

livestock2 <- window(livestock,start=1970,end=2000)
fit1 <- ses(livestock2)
fit2 <- holt(livestock2)
fit3 <- holt(livestock2,exponential=TRUE)
fit4 <- holt(livestock2,damped=TRUE)
fit5 <- holt(livestock2,exponential=TRUE,damped=TRUE)
# Results for first model:
fit1$model
accuracy(fit1) # training set
accuracy(fit1,livestock) # test set
plot(fit3, type="o", ylab="Livestock, sheep in Asia (millions)", 
  flwd=1, plot.conf=FALSE)
lines(window(livestock,start=2001),type="o")
lines(fit1$mean,col=2)
lines(fit2$mean,col=3)
lines(fit4$mean,col=5)
lines(fit5$mean,col=6)
legend("topleft", lty=1, pch=1, col=1:6,
    c("Data","SES","Holt's","Exponential",
      "Additive Damped","Multiplicative Damped"))

可以看出，holt和exponential两种方法在不同考察指标方面表现不一样，不同的考察指标可以选择不同的方法。

1.5 三次平滑 Holt-Winters seasonal method

1.5.1 加法和乘法模式additive Holt-Winters method & multiplicative Holt-Winters method

这种方法就是在两次平滑的基础上再考虑季节性因素，对季节性因素进行一次平滑

yt+h|tℓtbtst=ℓt+hbt+st−m+h+m=α(yt−st−m)+(1−α)(ℓt−1+bt−1)=β∗(ℓt−ℓt−1)+(1−β∗)bt−1=γ(yt−ℓt−1−bt−1)+(1−γ)st−m,

其中： h+m=⌊(h−1)mod m⌋+1 ,mod是求余数的意思， ⌊u⌋ 的意思是就个不大于u的最大整数
误差公式为：

ℓtbtst=ℓt−1+bt−1+αet=bt−1+αβ∗et=st−m+γet.

其中 et=yt−(ℓt−1+bt−1+st−m)=yt−yt|t−1
上面是加法形式，还有乘法形式:

yt+h|tℓtbtst=(ℓt+hbt)st−m+h+m.=αytst−m+(1−α)(ℓt−1+bt−1)=β∗(ℓt−ℓt−1)+(1−β∗)bt−1=γyt(ℓt−1+bt−1)+(1−γ)st−m

误差公式

ℓtbtst=ℓt−1+bt−1+αetst−m=bt−1+αβ∗etst−m=st+γet(ℓt−1+bt−1)

其中 et=yt−(ℓt−1+bt−1)st−m
其中乘法形式用在当季节性随时间成比例变化时
两种方法比较

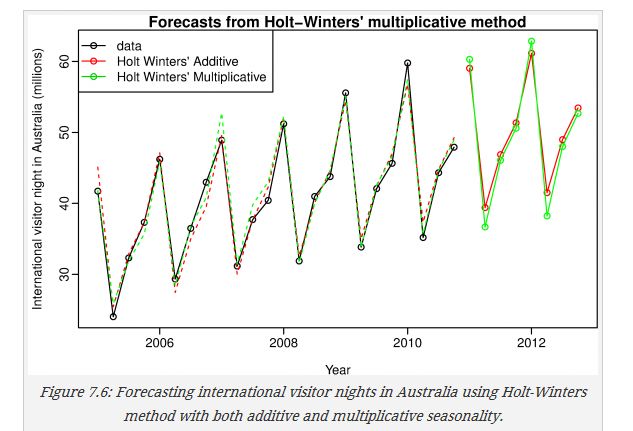
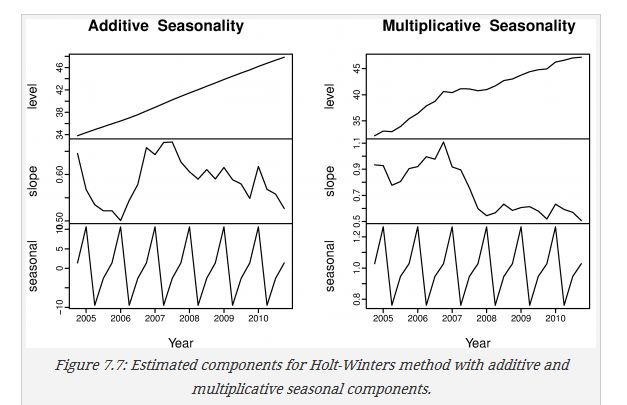
aust <- window(austourists,start=2005)
fit1 <- hw(aust,seasonal="additive")
fit2 <- hw(aust,seasonal="multiplicative")

plot(fit2,ylab="International visitor night in Australia (millions)",
     plot.conf=FALSE, type="o", fcol="white", xlab="Year")
lines(fitted(fit1), col="red", lty=2)
lines(fitted(fit2), col="green", lty=2)
lines(fit1$mean, type="o", col="red")
lines(fit2$mean, type="o", col="green")
legend("topleft",lty=1, pch=1, col=1:3, 
  c("data","Holt Winters' Additive","Holt Winters' Multiplicative"))

1.5.2 衰减模式Holt-Winters damped method

向前面一样，加入衰减因子，将h变为 (ϕ+ϕ2+⋯+ϕh)
具体方程：

yt+h|tℓtbtst=[ℓt+(ϕ+ϕ2+⋯+ϕh)bt]st−m+h+m.=α(yt/st−m)+(1−α)(ℓt−1+ϕbt−1)=β∗(ℓt−ℓt−1)+(1−β∗)ϕbt−1=γyt(ℓt−1+ϕbt−1)+(1−γ)st−m

1.6 15种指数平滑方法

上面提到了8中方法（加法和乘法算两种），其实类似的还有7种，根据trend和seasonal的处理方式可分为以下15种：

我们学过的8种：

他们的公式总结：

其初始值如果不使用优化方法，可做如下设置：

1.7 ETS

ETS就是在上面各种方法的基础之上加上了error项，error也有加法模式和乘法模式，与以上15种组合就得了30种模型！！！

1.7.1 30种模型

各模型公式

1.7.2 模型估计

除了之前的SSE还有最大似然法，在加法模式他们的结果是相同的

1.7.3 模型选择

如回归中对特征的选择的评价方法，这里也可以使用aic aicc bic等来评价
http://blog.csdn.net/bea_tree/article/details/51197704#t24

1.7.4 R 工具箱使用

ets

ets(y, model="ZZZ", damped=NULL, alpha=NULL, beta=NULL,
    gamma=NULL, phi=NULL, additive.only=FALSE, lambda=NULL,
    lower=c(rep(0.0001,3), 0.8), upper=c(rep(0.9999,3),0.98),
    opt.crit=c("lik","amse","mse","sigma","mae"), nmse=3,
    bounds=c("both","usual","admissible"),
    ic=c("aicc","aic","bic"), restrict=TRUE)

y

The time series to be forecast.

model

A three-letter code indicating the model to be estimated using the ETS classification and notation. The possible inputs are “N” for none, “A” for additive, “M” for multiplicative, or “Z” for automatic selection. If any of the inputs is left as “Z” then this component is selected according to the information criterion chosen. The default value of ZZZ ensures that all components are selected using the information criterion.

damped

If damped=TRUE, then a damped trend will be used (either Ad or Md). If damped=FALSE, then a non-damped trend will used. If damped=NULL (the default), then either a damped or a non-damped trend will be selected according to the information criterion chosen.

alpha, beta, gamma, phi

The values of the smoothing parameters can be specified using these arguments. If they are set to NULL (the default setting for each of them), the parameters are estimated.

additive.only

Only models with additive components will be considered if additive.only=TRUE. Otherwise all models will be considered.

lambda

Box-Cox transformation parameter. It will be ignored if lambda=NULL (the default value). Otherwise, the time series will be transformed before the model is estimated. When lambda is not NULL, additive.only is set to TRUE.

lower, upper

Lower and upper bounds for the parameter estimates α, β∗, γ∗ and ϕ.

opt.crit

The optimization criterion to be used for estimation. The default setting is maximum likelihood estimation, used when opt.crit=lik.

bounds

This specifies the constraints to be used on the parameters. The traditional constraints are set using bounds=”usual” and the admissible constraints are set using bounds=”admissible”. The default (bounds=”both”) requires the parameters to satisfy both sets of constraints.

ic

The information criterion to be used in selecting models, set by default to aicc.

restrict

If restrict=TRUE (the default), the models that cause numerical difficulties are not considered in model selection.

forecast

forecast(object, h=ifelse(object$m>1, 2*object$m, 10),
    level=c(80,95), fan=FALSE, simulate=FALSE, bootstrap=FALSE,
    npaths=5000, PI=TRUE, lambda=object$lambda, ...)

object

The object returned by the ets() function.

h

The forecast horizon — the number of periods to be forecast.

level

The confidence level for the prediction intervals.

fan

If fan=TRUE, level=seq(50,99,by=1). This is suitable for fan plots.

simulate

If simulate=TRUE, prediction intervals are produced by simulation rather than using algebraic formulae. Simulation will be used even if simulate=FALSE if there are no algebraic formulae available for the particular model.

bootstrap

If bootstrap=TRUE and simulate=TRUE, then the simulated prediction intervals use re-sampled errors rather than normally distributed errors.

npaths

The number of sample paths used in computing simulated prediction intervals.

PI

If PI=TRUE, then prediction intervals are produced; otherwise only point forecasts are calculated. If PI=FALSE, then level, fan, simulate, bootstrap and npaths are all ignored.

lambda

The Box-Cox transformation parameter. This is ignored if lambda=NULL. Otherwise, forecasts are back-transformed via an inverse Box-Cox transformation.

1.7.5 栗子

vndata <- window(austourists, start=2005)
fit <- ets(vndata)
summary(fit)
plot(forecast(fit,h=8),
  ylab="International visitor night in Australia (millions)")