推荐系统公平性之FairMatch--一种基于图的提升推荐系统整体多样性的方法
主要参考论文:《FairMatch A Graph-based Approach for Improving Aggregate Diversity in Recommender Systems》
什么是多样性
推荐系统中的多样性分为两类:
- 个体多样性(individual diversity)
指对于每一个用户而言,推荐结果是否具有多样性; - 整体多样性(aggregate diversity)
指对于整个推荐系统来说,它的推荐结果是否具有多样性。比如是否覆盖了足够多的物品,而不是只集中在小部分流行的物品。从这个角度上看,整体多样性就与之前提到的公平性中的流行度偏差属于一个范畴。
如何度量多样性
多样性的评价指标有很多,也可以根据不同的场景自行定义。这里列举几个:
针对个体多样性
- 推荐列表中物品两两间的不相似性
设物品两两间组合( C n 2 C_{n}^{2} Cn2)数量为N
多样性 = 1 - 每种组合的相似度之和 / N - 类别覆盖率(genre coverage)
如果多样性定义为推荐列表中物品的类型要尽可能的多,比如电影有喜剧类、动作类等等。 - 新颖性(novelty)
新颖性,顾名思义就是推荐结果可以让用户感觉很新鲜,是他以前都没见过的东西。这个指标也可以作为与多样性并列的指标,但是二者又密不可分。 - 惊喜性(serendipity)
从字面上与新颖性非常类似,但惊喜性不只强调推荐结果让用户感觉很新鲜,还要让用户感觉满意。可以类别一下惊吓和惊喜。
针对整体多样性
思路都是让尽可能多的物品推荐给用户,而不局限于小部分物品。
- 覆盖率(coverage)
指在所有用户的推荐列表中,至少出现过一次的物品占物品总数的多少。按照经验,常规的推荐算法覆盖率都比较低,尤其是top-K的K值较小时。 - 熵(entropy)
从信息论的角度,不确定越大,就是物品分布越均匀,那么熵就应该越大。物品分布越均匀,就意味着物品被推荐的几率越平等,所以这个指标在某种程度上比覆盖率更好,因为覆盖率对于被推荐一次和被推荐多次的物品是没有区分的。
物品的分布:p(i|L)=物品i在所有用户推荐列表中出现的次数 / (用户数×K)
论文的算法流程
算法的流程采用常规的后处理(post-processing)方法,即在常规推荐系统推荐结果的基础上进行重排。
- 用常规推荐系统为每个用户推荐t(t >> K)个物品;
- 用这些用户-物品构建二部图,执行最大流算法,找到低曝光率高相关性的候选物品集;
- 重新排序,用候选物品集中的物品替换掉t个物品中最流行的那部分物品,为每个用户推荐K个物品。
推荐系统中的最大流问题定义
传统最大流问题
以《算法导论》中的例子来简要说明:
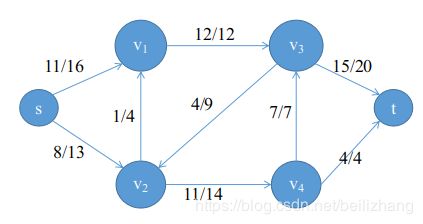
如上图所示,s为一个工厂(源结点),t为工厂的仓库(汇点),工厂每天要向仓库运送一定量的货物,v1,…,v4为运送途中要经过的城市。各边表示城市间的道路,都是单向的,边上的两个数字(*/*),左边的数字表示这条路上的实际货物数量,右边的数字这条道路最多允许有多少货物数量。最大流问题要解决的就是,工厂s每天最多生产多少货物运送到仓库t,且各条道路都不超过它的容量。
这个问题乍一看可能觉得只需要让每条道路都达到最大容量就行了,但其实不然。因为在最大流问题中,除了有道路的容量限制以外,还要满足流量守恒,即进入每个城市的货物数要等于该城市运出的货物数,否则会造成货物堆积。比如强行让(v2,v4)这条道路货物数达到最大值14,但是v4的输出能力却只有7+4=11,那么就会造成3件货物堆积在v4。
具体解法这里不赘述,读者可查阅《算法导论》或其他相关资料。
推荐系统中的最大流问题
这是论文作者定义的,将用户-物品二部图表示为一个最大流问题。(我并没有看太懂,加上感觉论文中的部分图有误,所以对论文有所质疑,这里先挖个坑,以后填~)
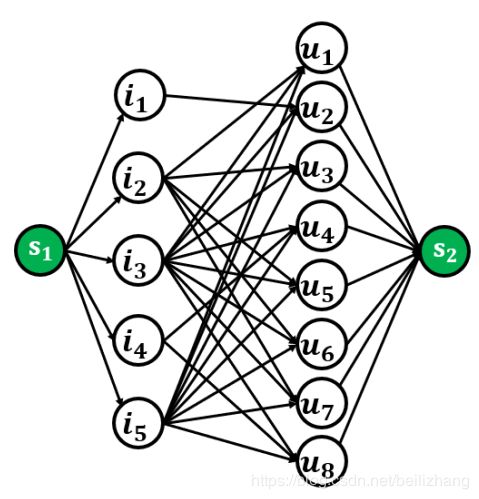
如上图所示,i1,…,i5表示物品,u1,…,u8表示用户,s1是源结点,s2是汇点。论文采用Push-relabel算法来解这个问题,这里只讲核心。
首先计算边的权重,也就是道路容量。
对于(i*,u*)这些边,权重=α×物品i的出度+(1-α)×物品i在用户u推荐列表中的排名。可以看到,如果一个物品越不流行(即被推荐的次数少,出度小)或者物品在用户列表中的排名很靠前(即rank值小),那么这条边的权重就越小,即道路容量越小。
对于(s1,i*)这些边,权重都是相等的,论文中给出了具体的值,我觉得选择一个合适的值就行。
对于(u*,s2)这些边,权重也是相等的,根据论文中的公式,比(s1,i*)的权重大。
然后定义结点的高度。s1的高度为整个图的结点总数|U|+|I|+2,u的高度都为2,i的高度都为1,s2的高度为0。因为Push-relabel算法是模拟水流在管道中流动,所以这样定义可以让流从s1流向s2。
让s1的水流流向i,如果i的输出能力不够,则会在i处堆积。如上面所述,这部分输出能力不够的结点,就意味着他们连接向u的边的权重不够高,排名太靠前和曝光率太低都是可能的原因,所以它们就是我们想找的低曝光率高相关性的物品。
文献链接
- 《FairMatch A Graph-based Approach for Improving Aggregate Diversity in Recommender Systems》
希望我的文章可以给你们的工作或者学习带来一丝灵感,共勉~