二分搜索树(Binary Search Tree) 笔记总结—— C++
查找问题的基础:二分查找法(对于有序数列,才能用二分查找法)
二分查找法:对于一个有序数组,我们想查找某一元素,先查看数组中间元素 v ,若 v 等于我们想查找的元素,那么我们找到了,否则的话,整个数组就被 v 这个元素分成了两个部分,小于 v 和大于 v 的部分,如果我们查找的元素是比 v 小的,我们就在小于 v 的这部分继续查找,要是比 v 大,就在大于 v 的部分查找。
二分查找法时间复杂度:O(log n)
代码:
//二分查找法,在有序数组arr中,查找target
//如果找到target,返回相应的索引index
//如果没有找到target,返回-1
template
int binarySearch(T arr[], int n, T target){
// 在arr[l...r]之中查找target
int l = 0, r = n-1;
while( l <= r ){
//int mid = (l + r)/2;要考虑溢出情况
int mid = l + (r-l)/2;
if( arr[mid] == target )//中间元素就是要寻找的元素
return mid;
if( arr[mid] > target )
r = mid - 1;
else
l = mid + 1;
}
//找到会在前面提前 return ,没找到才会执行到这里
return -1;
}
// 用递归的方式写二分查找法
template
int binarySearch2(T arr[], int l, int r, T target){
if( l > r )
return -1;
int mid = (l+r)/2;
if( arr[mid] == target )
return mid;
else if( arr[mid] > target )
return binarySearch2(arr, 0, mid-1, target);
else
return binarySearch2(arr, mid+1, r, target);
}
二分搜索树的优势:
1.高效,不仅可查找数据,还可以高效的插入,删除数据-动态维护数据
2.可以方便地回答很多数据间地关系问题:min max floor ceil rank select
二分搜索树定义:1.是二叉树;2.每个节点的键值大于左孩子,小于右孩子;3.以左右孩子为根的子树仍为二分搜索树
注意:二分搜索树不一定是完全二叉树
代码:
// key 是键相应的类型,value 是值相应的类型
template
class BST{
private:
//节点结构体
struct Node{//存储 key value 左右孩子
Key key;
Value value;
Node *left;
Node *right;
//结点的构造函数
Node(Key key, Value value){
this->key = key;
this->value = value;
this->left = this->right = NULL;
}
};
Node *root;//指向根部的节点
int count;//记录存储多少数据
// 向以 node 为根的二叉搜索树中,插入节点(key, value)
// 返回插入新节点后的二叉搜索树的根
Node* insert(Node *node, Key key, Value value){
// 递归到底,最基本的情况
if( node == NULL ){
count ++;
return new Node(key, value);
}
//先检查一下 key 是否等于 node 对应的 key
//等于的话相当于更新
if( key == node->key )
node->value = value;
//如果 key 小于 node 对应的 key
//向 node 的左子树相应的插入 (key, value)
//插入之后返回结果的这个根就应该返回给 node 的左子树
else if( key < node->key )
node->left = insert( node->left , key, value);
else // key > node->key
node->right = insert( node->right, key, value);
//返回节点本身
return node;
}
// 在以node为根的二叉搜索树中查找key所对应的value
Value* search(Node* node, Key key){
if( node == NULL )
return NULL;
if( key == node->key )
return &(node->value);
else if( key < node->key )
return search( node->left , key );
else // key > node->key
return search( node->right, key );
}
public:
BST(){
root = NULL;
count = 0;
}
~BST(){
// TODO: ~BST()
}
int size(){
return count;
}
bool isEmpty(){
return count == 0;
}
//插入操作
//将插入数据与根比较
//若数据小于根,尝试将数据插入到根的左子二叉树中
//若数据大于根,尝试将数据插入到根的右子二叉树中
//将左孩子或右孩子当作根,继续尝试插入
//直到出现与数据比较的孩子为空孩子时,将数据放到该位置
//若数据已存在,将原先数据用新的数据覆盖
void insert(Key key, Value value){
//向以 root 为根的二叉树插入 (key,value)这个数据对
//返回值为插入这个节点后得到的搜索树的根
root = insert(root, key, value);
}
//查找操作
// 查看以 node 为根的二叉搜索树中是否包含键值为 key 的节点
bool contain(Node* node, Key key){
//递归到底
if( node == NULL )
return false;
if( key == node->key )
return true;
else if( key < node->key )
return contain( node->left , key );
else // key > node->key
return contain( node->right , key );
}
Value* search(Key key){
return search( root , key );
}
};
二分搜索树的深度优先遍历:
前序遍历:先访问当前节点,再依次递归访问左右子树
中序遍历:先递归访问左子树,再访问自身,再递归访问右子树
(打印出来的数据从小到大排序,原因是左子树 < 根节点 < 右子树)
后序遍历:先递归访问左右子树,再访问自身节点
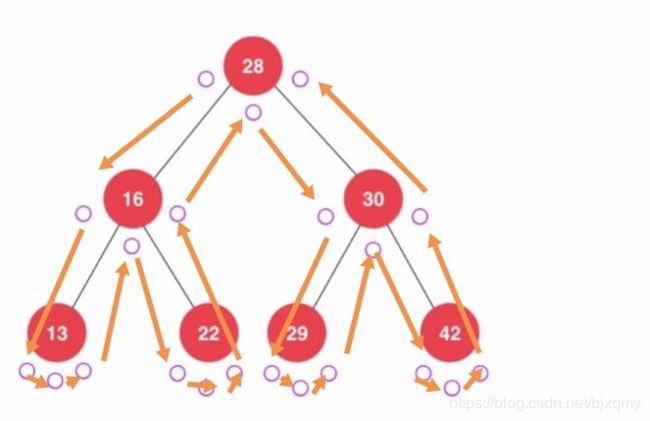
前序遍历实现:访问顺序如下,若访问到左边的圆点,则将数据打印
打印结果为 28 16 13 22 30 29 42
中序遍历实现:访问顺序如下,若访问到中间的圆点,则将数据打印
打印结果为 13 16 22 28 29 30 42
后序遍历实现:访问顺序如下,若访问到右边的圆点,则将数据打印
打印结果为 13 22 16 29 42 30 28
代码:
template
class BST{
private:
。
。
。
// 对以node为根的二叉搜索树进行前序遍历
void preOrder(Node* node){
if( node != NULL ){
cout<key<left);
preOrder(node->right);
}
}
// 对以node为根的二叉搜索树进行中序遍历
void inOrder(Node* node){
if( node != NULL ){
inOrder(node->left);
cout<key<right);
}
}
// 对以node为根的二叉搜索树进行后序遍历
void postOrder(Node* node){
if( node != NULL ){
postOrder(node->left);
postOrder(node->right);
cout<key<left );
destroy( node->right );
delete node;
count --;
}
}
public:
。
。
。
// 前序遍历
void preOrder(){
preOrder(root);
}
// 中序遍历
void inOrder(){
inOrder(root);
}
// 后序遍历
void postOrder(){
postOrder(root);
}
};
二分搜索树的广度优先遍历(层序遍历):
引入队列的概念(元素先进先出,后进后出)
操作:元素入队,出队时将其左右孩子入队,持续这个循环,直到队列为空。
注意:开始时将根元素入队;若没有孩子时,跳过孩子入队部分,接着下个元素出队
代码:
#include
#include
using namespace std;
template
class BST{
private:
。
。
。
public:
。
。
。
// 层序遍历,引入队列 #include 头文件
void levelOrder(){
//声明队列 q ,存放的是 Node* 这样的对象
queue q;
//入队根节点
q.push(root);
while( !q.empty() ){
//取出队首元素
Node *node = q.front();
//令队首元素出队
q.pop();
//将 node 元素的键值打印出来
cout<key<left )
q.push( node->left );
//有右孩子,右孩子入队
if( node->right )
q.push( node->right );
}
}
};
二分搜索树 删除最大值最小值节点:
1.删除最小值:从根节点开始,不停的沿着它的左孩子的方向查找,直到有一个节点再也没有左孩子,那么这个节点一定就是这棵二分搜索树的最小值
2.删除最大值:从根节点开始,不停的沿着它的右孩子的方向查找,直到有一个节点再也没有右孩子,那么这个节点一定就是这棵二分搜索树的最大值
代码:
template
class BST{
private:
。
。
。
// 在以node为根的二叉搜索树中,返回最小键值的节点
Node* minimum(Node* node){
if( node->left == NULL )
return node;
return minimum(node->left);
}
// 在以node为根的二叉搜索树中,返回最大键值的节点
Node* maximum(Node* node){
if( node->right == NULL )
return node;
return maximum(node->right);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
Node* removeMin(Node* node){
//如果其有右孩子,左孩子为空
//则将其右孩子代替删除的节点,成为这个已经被删除节点的父节点的新的左孩子
if( node->left == NULL){
Node* rightNode = node->right;
delete node;
count --;
return rightNode;
}
node->left = removeMin(node->left);
return node;
}
// 删除掉以node为根的二分搜索树中的最大节点
// 返回删除节点后新的二分搜索树的根
Node* removeMax(Node* node){
if( node->right == NULL ){
Node* leftNode = node->left;
delete node;
count --;
return leftNode;
}
node->right = removeMax(node->right);
return node;
}
public:
。
。
。
// 寻找最小的键值
Key minimum(){
//保证二叉树不为空
assert( count != 0 );
Node* minNode = minimum( root );
return minNode->key;
}
// 寻找最大的键值
Key maximum(){
assert( count != 0 );
Node* maxNode = maximum(root);
return maxNode->key;
}
// 从二叉树中删除最小值所在节点
void removeMin(){
if( root )
root = removeMin( root );
}
// 从二叉树中删除最大值所在节点
void removeMax(){
if( root )
root = removeMax( root );
}
};
二分搜索树 删除任意指定节点:
操作:
1.删除只有左孩子的节点:删除该节点,并让该节点的左孩子代替其成为其父节点的孩子
2.删除只有右孩子的节点:删除该节点,并让该节点的右孩子代替其成为其父节点的孩子
3.删除既有左孩子又有右孩子的节点 d :(左子树最大节点也可以)
- 找到右子树中最小节点 s = min(d-right) 作为 d 的后继
- 调用delMin() 函数,将 s 这个节点从原来的子树上删除掉
- s 节点的右边指向原来节点的右子树, s->right =delMin(d->right)
- s 节点的左孩子就是 d 的左孩子
- delete d ,s 成为新子树的根
代码:
template
class BST{
private:
struct Node{
。
。
。
Node(Node *node){
this->key = node->key;
this->value = node->value;
this->left = node->left;
this->right = node->right;
}
};
。
。
。
// 删除掉以node为根的二分搜索树中键值为key的节点
// 返回删除节点后新的二分搜索树的根
Node* remove(Node* node, Key key){
if( node == NULL )
return NULL;
if( key < node->key ){
node->left = remove( node->left , key );
return node;
}
else if( key > node->key ){
node->right = remove( node->right, key );
return node;
}
else{ // key == node->key
//只有右孩子
if( node->left == NULL ){
Node *rightNode = node->right;
delete node;
count --;
return rightNode;
}
if( node->right == NULL ){
Node *leftNode = node->left;
delete node;
count--;
return leftNode;
}
// node->left != NULL && node->right != NULL
//successor 为删除节点的后继
//将 node 右子树中的最小值复制一份,所以要在 node 结构体中创建一个新的构造函数
Node *successor = new Node(minimum(node->right));
//创建了一个新的节点,所以要维护一下 count
count ++;
successor->right = removeMin(node->right);
successor->left = node->left;
delete node;
count --;
return successor;
}
}
public:
。
。
。
// 从二叉树中删除键值为key的节点
void remove(Key key){
root = remove(root, key);
}
};
二分搜索树的局限性:一组数据,可对应不同的二分搜索树,导致其可能退化成链表
优化:平衡二叉树:节点左右子树高度的差不超过 1,典型的一种实现为红黑树
红黑树:创新地将节点分为了两类节点,一类叫作红色节点,一类叫作黑色节点
在插入或者删除中将考虑这个节点地颜色进行一系列的改变