TSP-粒子群算法求解
1、粒子群算法
(1)起源
该算法最初是受到飞鸟集群活动的规律性启发,进而利用群体智能建立的一个简化模型。
(2)概念
粒子群算法,也称粒子群优化算法或鸟群觅食算法(Particle Swarm Optimization),缩写为 PSO,是一种全局优化算法。鸟群在整个搜寻的过程中,通过相互传递各自的信息,让其他的鸟知道自己的位置,通过这样的协作,来判断自己找到的是不是最优解,同时也将最优解的信息传递给整个鸟群,最终,整个鸟群都能聚集在食物源周围,即找到了最优解。在PSO中,每只鸟的位置都是优化问题解空间中的一个解。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitness value),每个粒子还有一个速度决定它们飞翔的方向和速率。然后,粒子们就追随当前的最优粒子在解空间中搜索。在初始化阶段,PSO生成一群随机粒子(即随机解),然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个"极值"来更新自己。第一个极值就是粒子本身所找到的历史最优解,这个解叫做个体极值pBest。另一个极值是整个种群找到的历史最优解,这个极值是全局极值gBest。
(3)粒子公式

公式(1)的第①部分称为【记忆项】,表示上次速度大小和方向的影响;第②部分称为【自身认知项】,是从当前点指向粒子自身最好点的一个矢量,表示粒子的动作来源于自己经验的部分;第③部分称为【群体认知项】,是一个从当前点指向种群最好点的矢量,反映了粒子间的协同合作和知识共享。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。
以上面两个公式为基础,再来看一个公式

公式(2)和(3)被视为标准的PSO算法
注:
(1)当c_1=0时,则粒子没有了认知能力,变为只有社会模型。此时的PSO称为全局PSO算法。粒子有扩展搜索空间的能力,具有较快的收敛速度,但由于缺少局部搜索,对于复杂问题比标准PSO 更易陷入局部最优
(2)当c_2=0时,则粒子之间没有社会信息,模型变为只有认知模型。此时的PSO称为局部PSO算法。由于个体之间没有信息的交流,整个群体相当于多个粒子进行盲目的随机搜索,收敛速度慢,因而得到最优解的可能性小。
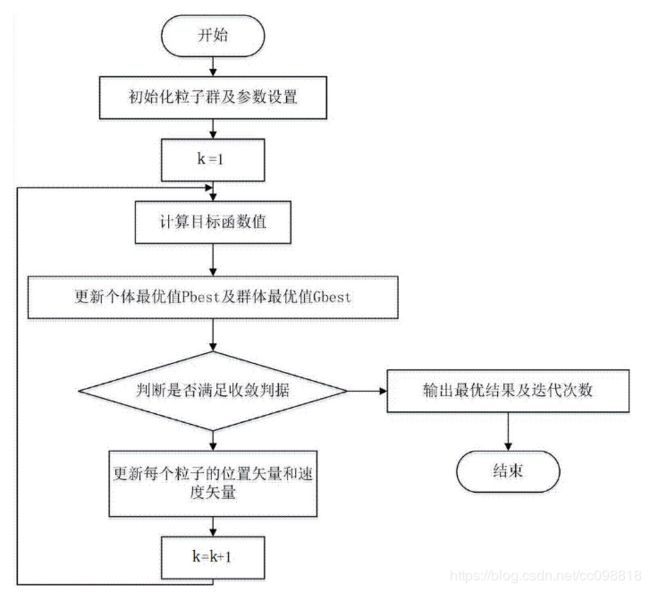
(4)流程
**第一步:**初始化一群粒子(群体规模为N),包括随机位置和速度;
**第二步:**评价每个粒子的适应度;
**第三步:**对每个微粒,将其适应值与其经过的最好位置pbest作比较,如果较好,则将其作为当前的最好位置pbest;
**第四步:**对每个微粒,将其适应值与其经过的最好位置gbest作比较,如果较好,则将其作为当前的最好位置gbest;
**第五步:**根据公式(2)、(3)调整微粒速度和位置;
**第六步:**未达到结束条件则转第二步。
注:终止条件根据具体问题一般选为最大迭代次数或(和)微粒群迄今为止搜索到的最优位置满足预定最小适应阈值。
(5)流程图
(6)简单实例
下面用PSO算法求解函数y=-x*(x-2) 在[0,2]上最大值(最大值在x=1取到,为1)
package cn.chb;
public class PSO {
public int n;//粒子个数,这里为了方便演示,我们只取两个,观察其运动方向
public int c1;//学习因子
public int c2;//学习因子
public double vmax;//粒子的最大速度
public double[]x;//粒子的x坐标
public double[]y;//粒子的x坐标
public double[]v;//粒子的速度
public double[]pbest;//粒子的历史最优解
public double gbest;//群体最优解
//初始化
public void init() {
n=2;
c1=2;
c2=2;
vmax=0.1;
x=new double[n];
x[0]=0.0;
x[1]=2.0;
y=new double[n];
caculateFitness();
v=new double[n];
v[0]=0.01;
v[0]=0.02;
pbest=new double[n];
for (int i = 0; i < n; i++) {
pbest[i]=y[i];
if(pbest[i]>gbest) {
gbest=pbest[i];
}
}
System.out.println("算法开始,起始最优解:"+gbest);
System.out.println();
}
//适应度计算函数,每个粒子都有它的适应度
public void caculateFitness() {
for (int i = 0; i < n; i++) {
y[i]=-1*x[i]*(x[i]-2);
}
}
//去两个数的最大值
public double getMAX(double a,double b){
return a>b?a:b;
}
//粒子群算法
public void Pso(int max) {
for (int i = 0; i < max; i++) {
double w=0.4;
for (int j = 0; j < n; j++) {
//更新位置和速度,就是公式(2)和(3)
v[j]=w*v[j]+c1*Math.random()*(pbest[j]-x[j])+c2*Math.random()*(gbest-x[j]);
if(v[j]>vmax) {
v[j]=vmax;//控制速度不超过最大值
}
x[j]+=v[j];
//越界判断,范围限定在[0, 2]
if(x[j]>2) {
x[j]=2;
}
if(x[j]<0) {
x[j]=0;
}
}
caculateFitness();
//更新个体极值和群体极值
for (int j = 0; j < n; j++) {
pbest[j]=getMAX(y[j],pbest[j]);
if(pbest[j]>gbest) {
gbest=pbest[j];
}
System.out.println("粒子n"+j+": x = "+x[j]+" "+"v = "+v[j]);
}
System.out.println("第"+(i+1)+"次迭代,全局最优解 gbest = "+gbest);
System.out.println();
}
}
public static void main(String[] args) {
PSO pso=new PSO();
pso.init();
pso.Pso(10);//为了方便演示,我们暂时迭代10次
}
}
运行结果:
算法开始,起始最优解:0.0
粒子n0: x = 0.008 v = 0.008
粒子n1: x = 0.0 v = -4.477087151378778
第1次迭代,全局最优解 gbest = 0.015936
粒子n0: x = 0.032543190251566295 v = 0.02454319025156629
粒子n1: x = 0.0 v = -1.7808210799382407
第2次迭代,全局最优解 gbest = 0.06402732127138296
粒子n0: x = 0.08231990967327549 v = 0.049776719421709185
粒子n1: x = 0.0 v = -0.6430831068179309
第3次迭代,全局最优解 gbest = 0.15786325181793476
粒子n0: x = 0.1823199096732755 v = 0.1
粒子n1: x = 0.0 v = -0.18916117763913753
第4次迭代,全局最优解 gbest = 0.33139926988327967
粒子n0: x = 0.28231990967327547 v = 0.1
粒子n1: x = 0.1 v = 0.1
第5次迭代,全局最优解 gbest = 0.4849352879486245
粒子n0: x = 0.38231990967327545 v = 0.1
粒子n1: x = 0.2 v = 0.1
第6次迭代,全局最优解 gbest = 0.6184713060139694
粒子n0: x = 0.4823199096732754 v = 0.1
粒子n1: x = 0.30000000000000004 v = 0.1
第7次迭代,全局最优解 gbest = 0.7320073240793143
粒子n0: x = 0.5823199096732754 v = 0.1
粒子n1: x = 0.4 v = 0.1
第8次迭代,全局最优解 gbest = 0.8255433421446592
粒子n0: x = 0.6823199096732754 v = 0.1
粒子n1: x = 0.5 v = 0.1
第9次迭代,全局最优解 gbest = 0.899079360210004
粒子n0: x = 0.7823199096732754 v = 0.1
粒子n1: x = 0.6 v = 0.1
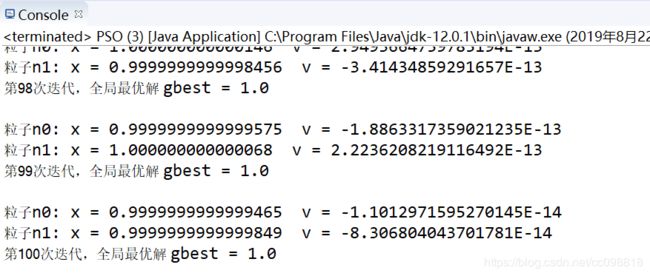
第10次迭代,全局最优解 gbest = 0.952615378275349
当迭代次数较大时,能找到最优解:
2、求解TSP
同样是求解att48实例(最优解为10628)
代码结构:
其中Data类表示定义数据、变量初始化和读取数据的类
package com.chb.Tabu;
import java.io.BufferedReader;
import java.io.FileNotFoundException;
import java.io.FileReader;
import java.util.ArrayList;
import java.util.Random;
import java.util.Scanner;
public class Data {
public static int cityNum=48;//城市数量,手动设置
public static final int MAX_GEN=5000;//运行代数
public static final float w=0.5f;//权重
public static int bestNum;
public static int scale=30;//种群规模
public static int t;//当前代数
public static int point[][]=new int[cityNum][2];//每个城市的坐标
public static int dist[][]=new int[cityNum][cityNum];//距离矩阵
public static int oppulation[][]=new int[scale][cityNum];//粒子群
public static ArrayList>listV;//每个粒子的初始交换序列
public static int[][]Pd=new int[scale][cityNum];//一个粒子历代中出现的最好的解
public static int[]vPd=new int[scale];//粒子的评价值
public static int[]Pgd=new int[cityNum];//整个粒子群经历过的最好的解,每个粒子都能记住自己搜索到的最好解
public static int vPgd;//最后的解的评价值
public static int bestT;//最佳出现代数
public static int[]fitness=new int[scale];//种群适应度,表示种群中各个个体的适应度
public static Random random;
//读取数据并初始化
public static void read_data(String filepath) throws FileNotFoundException {
String line=null;
String substr[]=null;
Scanner cin=new Scanner(new BufferedReader(new FileReader(filepath)));
for (int i = 0; i < cityNum; i++) {
line=cin.nextLine();
line.trim();
substr=line.split(" ");
point[i][0]=Integer.parseInt(substr[1]);//x坐标
point[i][1]=Integer.parseInt(substr[2]);//y坐标
}
cin.close();
//计算距离矩阵,注意这里的计算方式,才用的是伪欧式距离
for (int i = 0; i < cityNum; i++) {
dist[i][i]=0;//对角线元素为0
for (int j = i+1; j < cityNum; j++) {
double rij=Math.sqrt((Math.pow(point[i][0]-point[j][0], 2)+
Math.pow(point[i][1]-point[j][1], 2))/10.0);
//rij四舍五入取整
int tij=(int) Math.round(rij);
if(tij
SO类是蚂蚁类
package com.chb.Tabu;
public class SO {
private int x;
private int y;
public SO(int x, int y) {
super();
this.x = x;
this.y = y;
}
public int getX() {
return x;
}
public void setX(int x) {
this.x = x;
}
public int getY() {
return y;
}
public void setY(int y) {
this.y = y;
}
}
PSO类是算法的主体类
package com.chb.Tabu;
import java.io.FileNotFoundException;
import java.util.ArrayList;
public class PSO {
//初始化种群
public static void initGroup() {
int i,j,k;
for (k = 0; k >();
for (int i = 0; i < Data.scale; i++) {
ArrayListlist=new ArrayList();
ra=Data.random.nextInt(65535)%Data.cityNum;
for (int j = 0; j < ra; j++) {
raA=Data.random.nextInt(65535)%Data.cityNum;
raB=Data.random.nextInt(65535)%Data.cityNum;
while(raA==raB) {
raB=Data.random.nextInt(65535)%Data.cityNum;
}
SO s=new SO(raA,raB);
list.add(s);
}
Data.listV.add(list);
}
}
//评价函数
public static int evaluate(int[] chr) {
int len=0;
for (int i = 1; i < Data.cityNum; i++) {
len+=Data.dist[chr[i-1]][chr[i]];
}
len+=Data.dist[chr[Data.cityNum-1]][chr[0]];
return len;
}
// 求一个基本交换序列作用于编码arr后的编码
public static void add(int[]arr,ArrayListlist) {
int temp=-1;
SO s;
for (int i = 0; i < list.size(); i++) {
s=list.get(0);
temp=arr[s.getX()];
arr[s.getX()]=arr[s.getY()];
arr[s.getY()]=temp;
}
}
// 求两个编码的基本交换序列,如A-B=SS
public static ArrayListminus(int[]a,int[]b){
int[]temp=b.clone();
int index;
SO s;
ArrayList list=new ArrayList();
for (int i = 0; i < Data.cityNum; i++) {
if(a[i]!=temp[i]) {
// 在temp中找出与a[i]相同数值的下标index
index=findNum(temp,a[i]);
// 在temp中交换下标i与下标index的值
changeIndex(temp, i, index);
// 记住交换子
s = new SO(i, index);
// 保存交换子
list.add(s);
}
}
return list;
}
// 在arr数组中查找num,返回num的下标
public static int findNum(int[]arr,int num) {
int index=-1;
for (int i = 0; i < Data.cityNum; i++) {
if(arr[i]==num) {
index=i;
break;
}
}
return index;
}
// 将数组arr下标index1与下标index2的值交换
public static void changeIndex(int[]arr,int index1,int index2) {
int temp=arr[index1];
arr[index1]=arr[index2];
arr[index2]=temp;
}
//二维数组拷贝
public static void copyarray(int[][]a,int[][]b) {
for (int i = 0; i < Data.scale; i++) {
for (int j = 0; j < Data.cityNum; j++) {
b[i][j]=a[i][j];
}
}
}
//一维数组拷贝
public static void copyarrayNum(int[]a,int[]b) {
for (int i = 0; i < Data.cityNum; i++) {
b[i]=a[i];
}
}
public static void evolution() {
int i,j,k;
int len=0;
float ra=0f;
ArrayListVi;
//迭代一次
for (int t = 0; t < Data.MAX_GEN; t++) {
//对于每颗粒子
for (i = 0; i < Data.scale; i++) {
if(i==Data.bestNum) {
continue;
}
ArrayListVii=new ArrayList();
Vi=Data.listV.get(i);
len=(int) (Vi.size()*Data.w);
for ( j = 0; j < len; j++) {
Vii.add(Vi.get(j));
}
// Pid-Xid
ArrayList a = minus(Data.Pd[i], Data.oppulation[i]);
ra = Data.random.nextFloat();
// ra(Pid-Xid)+
len = (int) (a.size() * ra);
//越界判断
for (j = 0; j < len; j++) {
Vii.add(a.get(j));
}
// Pid-Xid
ArrayList b = minus(Data.Pgd, Data.oppulation[i]);
ra = Data.random.nextFloat();
// ra(Pid-Xid)+
len = (int) (b.size() * ra);
//越界判断
for (j = 0; j < len; j++) {
SO tt= b.get(j);
Vii.add(tt);
}
//保存Vii
Data.listV.add(i,Vii);
// 更新位置
add(Data.oppulation[i], Vii);
// 计算新粒子群适应度,Fitness[max],选出最好的解
for (k = 0; k < Data.scale; k++) {
Data.fitness[k] = evaluate(Data.oppulation[k]);
if (Data.vPd[k] > Data.fitness[k]) {
Data.vPd[k] = Data.fitness[k];
copyarrayNum(Data.oppulation[k], Data.Pd[k]);
Data.bestNum=k;
}
if (Data.vPgd > Data.vPd[k]) {
//System.out.println("最佳长度"+Data.vPgd+" 代数:"+Data.bestT);
Data.bestT = t;
Data.vPgd = Data.vPd[k];
copyarrayNum(Data.Pd[k], Data.Pgd);
}
}
}
}
}
public static void solve() {
int i;
int k;
initGroup();
initListV();
// 每颗粒子记住自己最好的解
copyarray(Data.oppulation, Data.Pd);
// 计算初始化种群适应度,Fitness[max],选出最好的解
for (k = 0; k < Data.scale; k++) {
Data.fitness[k] = evaluate(Data.oppulation[k]);
Data.vPd[k] = Data.fitness[k];
if (Data.vPgd > Data.vPd[k]) {
Data.vPgd = Data.vPd[k];
copyarrayNum(Data.Pd[k], Data.Pgd);
Data.bestNum=k;
}
}
// 打印
// System.out.println("初始粒子群...");
// for (k = 0; k < Data.scale; k++) {
// for (i = 0; i < Data.cityNum; i++) {
// System.out.print(Data.oppulation[k][i] + ",");
// }
// System.out.println();
// System.out.println("----" + Data.fitness[k]);
// }
// 进化
evolution();
// 打印
// System.out.println("最后粒子群...");
// for (k = 0; k < Data.scale; k++) {
// for (i = 0; i < Data.cityNum; i++) {
// System.out.print(Data.oppulation[k][i] + ",");
// }
// System.out.println();
// System.out.println("----" + Data.fitness[k]);
// }
System.out.println("最佳长度出现代数:"+Data.bestT);
System.out.println("最佳长度"+Data.vPgd);
System.out.println("最佳路径:");
for (i = 0; i < Data.cityNum; i++) {
System.out.print(Data.Pgd[i] + "-->");
}
}
public static void main(String[] args) throws FileNotFoundException {
Data.read_data("data/att48.txt");
PSO.solve();
}
}
data文件夹中的att48.txt是测试文件,可直接百度TSPLIB下载,或从https://pan.baidu.com/s/1Pc71mAN7WBbdxkzOkOK8gw处下载
运行结果:

分析:这个实验结果很差,原因出在迭代公式上,以后有时间再优化
注:本文提炼、转载自
[1]https://blog.csdn.net/wangqiuyun/article/details/12515203
[2]https://mp.weixin.qq.com/s?__biz=MzU0NzgyMjgwNg==&mid=2247485031&idx=1&sn=7431c3937e66bf3f8f383eb8f088f6f3&chksm=fb49cbdecc3e42c8f38d1af4ae67c6c667350605bc7a01c26a4ac4b53f4207c156dfe09ed104&mpshare=1&scene=1&srcid=0822pVkjBrc3Z6hBfKflSkNn&sharer_sharetime=1566433694416&sharer_shareid=054592193644de509623829748e83807&key=5c697a296e1d5a5c77e9aab85df6cf52cb48d9f4dfadc09bce1ab7644261e5b6b451806e6c8d6e58e4cb08b22ec02421d923a21932c520f029d0a52d62971bfdffcac0dcf87536336aeb1205cca7ed28&ascene=1&uin=MjYzMDA1MzAyMQ%3D%3D&devicetype=Windows+10&version=62060834&lang=zh_CN&pass_ticket=u%2FFCYZF31oHuOVDtiAk9qU93vdWJIhzB98r7dHrcOYBSBGJ242N951lTB%2F35LG4A