十月的最后一天啦!还是要元气满满鸭!今天初步学习了感知器和激活函数,故做如下记录。
感知器(Perception)
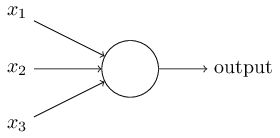
什么是感知器呢?通过图片来直观感受一下。
通过图片可以看出,感知器在图形直观上是接受多个input,最后只得到一个output的一个机器,相当于一个黑盒函数,它可能会有很多隐藏层(扣除input和output外的内部层),它的本质其实可以理解为决策。
举个简单的栗子:
比如你想要买一套房子,x1是价钱因素,x2是地理位置,x3是配套设施,这三个条件各占的比重不一样,把A地块的房子的三个条件输入到感知器中,然后就能得到感知器给我们决策的结果,而感知器内部决策的原理,其实就是给不同的因素赋予不同的权重,因为不同的因素的重要性对买房者来说,自然是不相同的。然后设置一个阈值,如果加权计算之后的结果大于等于这个阈值,就说明可以判断为要买房,否则则是不买房。
所以感知器本质上就是一个通过加权计算函数进行决策的工具。
再举个实用的例子:
我们设计一个感知器,让它来实现and运算。真值表如下:
解答这个问题,可以先把上面例子的那个公式(阶跃函数)化简后在求解:
这个时候我们可以利用公式来验证:
f(y)=f(w·x+b)=f(0.5*0+0.5*0-0.8)=f(-0.8<0)=0
f(y)=f(w·x+b)=f(0.5*0+0.5*1-0.8)=f(-0.3<0)=0
f(y)=f(w·x+b)=f(0.5*1+0.5*0-0.8)=f(-0.3<0)=0
f(y)=f(w·x+b)=f(0.5*1+0.5*1-0.8)=f(0.2>0)=1
经过验证是符合的。
通过两个例子,可以发现感知器的学习过程就是通过改变感知器内部的权重和偏移。(也就是w和b)
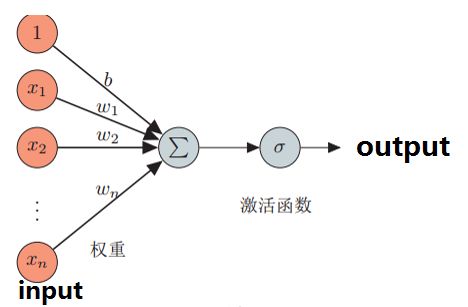
而中间还需要引入函数,产生最终的输出。那么完整的感知器模型是这样的:
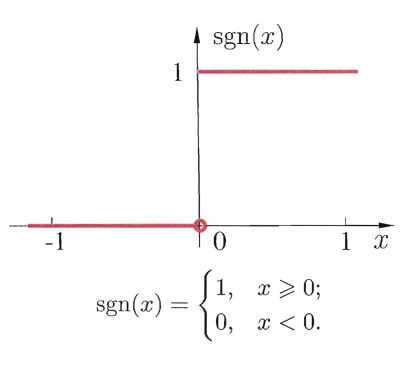
例子中举到的函数是阶跃函数,属于一个较为理想也可以说是离散型的函数,非1即0
问题就出现了,这样的话,阶跃函数不连续不光滑,如果我们稍微改变权重或者偏移,得到的结果就是要么不变,要么就感知器的输出彻底相反。而我们原本期望的是,每个感知器都对输出结果有一定的比重的贡献,单个感知器权重或偏移的变化应该是对输出结果产生微小影响的。所以这个时候我们需要激活函数。
激活函数
激活函数就是在感知器加权计算之后,再输入到激活函数中进行计算,得到一个输出。
激活函数的特点或者说作用是在于 :可以使得输出结果变得非线性化(加入非线性因素)
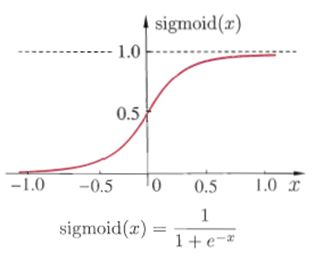
先举个激活函数的例子:sigmoid函数
函数特点:把一个实数压缩至0到1之间。当z是非常大的正数时,g(z)会趋近于1,而z是非常大的负数时,则g(z)会趋近于0。
好处分类的概率,比如激活函数的输出为0.9的话便可以解释为90%的概率为正样本。
加入感知器后的函数形式和图像如下:
这个时候就会看到一个较为光滑连续的图像了。
接下来通过图像我们可以直观的看出作用:
从图像可以很明显的发现,激活函数的加入可以解决分类的时候,非线性问题。
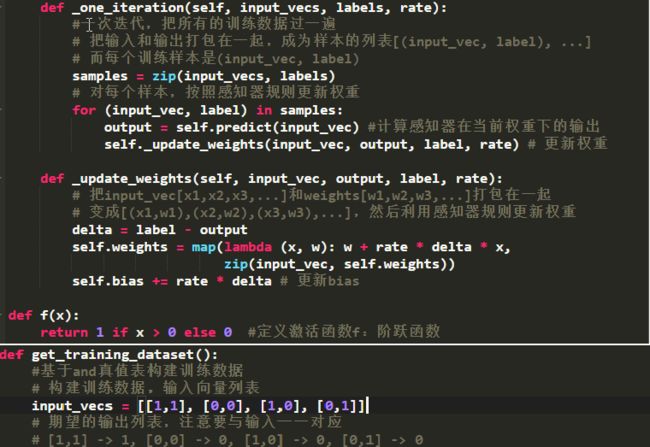
最后用Python做一个刚刚的检验and函数真值表的实现。
代码如下:
输出结果:
参考来源:‘
神经网络’初探 -
python 实现感知器(一) - lilong117194的博客 - CSDN博客
finally~十月收官!
十一月也要坚持鸭!