面试题11：旋转数组的最小数字

旋转数组的最小数字

• LeetCode链接： 153. Find Minimum in Rotated Sorted Array
  

题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组 {3,4,5,1,2} 为 {1,2,3,4,5} 的一个旋转，该数组的最小值为 1。

注意： 给出的所有元素都大于0，若数组大小为 0，请返回 0。

思路一：直接比较

数组旋转后相当于组成两个非递减的子数组，只需要遍历一遍找到 nums[i-1] > nums[i]，就可以确定 nums[i] 是旋转数组的最小元素。

class Solution {
    public int findMin(int[] nums) {
        if (nums == null || nums.length == 0)
            return -1;
        for (int i = 1; i < nums.length; ++i) {
            if (nums[i] < nums[i - 1])
                return nums[i];
        }
        return nums[0];
    }
}

思路二：二分查找

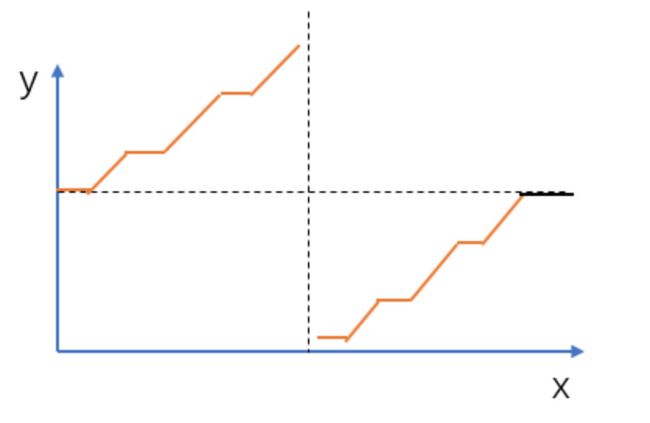
为了便于分析，我们先将数组中的元素画在二维坐标系中，横坐标表示数组下标，纵坐标表示数值，如下所示：

图中水平的实线段表示相同元素。注意题目中说数组中的元素是非减排序的。

我们发现除了最后水平的一段（黑色水平那段）之外，其余部分满足二分性质：

• 竖直虚线左边的数满足 nums[i] ≥ nums[0]；
• 竖直虚线右边的数不满足这个条件。
  分界点就是整个数组的最小值。

所以我们先将最后水平的一段删除即可。

另外，不要忘记处理数组 完全单调 的 特殊情况：
当我们删除最后水平的一段之后，如果剩下的最后一个数大于等于第一个数，则说明数组完全单调。

class Solution {
    public int findMin(int[] nums) {
        if (nums == null || nums.length == 0)
            return -1;
        int n = nums.length - 1;
        while (n > 0 && nums[0] == nums[n])
            --n;
        if (nums[n] >= nums[0])
            return nums[0];

        int l = 0, r = n;
        while (l < r) {
            int mid = (l + r) >>> 1;
            if (nums[mid] >= nums[0])
                l = mid + 1;
            else
                r = mid;
        }
        return nums[l];
    }
}

时间复杂度：

二分的时间复杂度是 $O(logn)$，删除最后水平一段的时间复杂度最坏是 $O(n)$，所以总时间复杂度是 $O(n)$。

参考链接：

• https://www.acwing.com/solution/LeetCode/content/247/

搜索旋转排序数组

• LeetCode链接： 33. Search in Rotated Sorted Array
  

题目描述

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2])。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是$O(logn)$ 级别。

样例

示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4

示例 2:

输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1

思路一：三次二分

第一次二分查找，找到数组中最小的元素下标，也就是将数组分割成两部分的枢纽 pivot。然后分别在 [0, povit) 和 [pivot,nums.length) 两个区间内二分查找 target

class Solution {
    public int search(int[] nums, int target) {
        if (nums == null || nums.length == 0)
            return -1;
        int pivot = binarySearch(nums, 0, nums.length, nums[0]);
        int leftPart = Arrays.binarySearch(nums, 0, pivot, target);
        int rightPart = Arrays.binarySearch(nums, pivot, nums.length, target);
        if (leftPart < 0 && rightPart < 0)
            return -1;
        return leftPart >= 0 ? leftPart : rightPart;
    }

    private int binarySearch(int[] nums, int low, int high, int target) {
        int l = low, r = high;
        while (l < r) {
            int mid = (l + r) >>> 1;
            // 找到第一个小于target的元素
            if (nums[mid] >= target) {
                l = mid + 1;
            } else {
                r = mid;
            }
        }
        return l;
    }
}

思路二：一次二分

1. 数组长度为 0 则直接返回 -1。

2. 每一次二分，我们具体看一下什么时候答案可能在 [l, mid] 中，什么时候答案可能在 [mid+1, r] 中。

3. 注意到 num[0] 是个非常关键的元素，已知数组被分为两个升序部分，且后半部分全部比 nums[0] 小，如果 nums[i]>=nums[0] 则说明 [0, i] 一定是升序的，否则 [i+1, n-1] 一定是升序的。还可以根据 target 与 nums[0] 的关系，判断出 target 可能属于哪一部分。

4. 根据 3，如果给定了一个位置 mid，我们可以根据 nums[0]、nums[mid] 与 target 三者的关系，确定出 target 可能属于哪一段区间。具体看代码注释部分。

class Solution {
    public int search(int[] nums, int target) {
        if (nums == null || nums.length == 0)
            return -1;
        int l = 0, r = nums.length - 1;
        while (l < r) {
            int mid = (l + r) >>> 1;
            if (nums[mid] >= nums[0]) { // mid在数组前半部分。
                if (target > nums[mid])
                    // 可以推出target的值一定大于nums[0]，target只可能在[mid+1, r]中。
                    l = mid + 1;
                if (target < nums[0])
                    // 可以推出target的值一定小于nums[mid]，target只可能在[mid+1, r]中。
                    l = mid + 1;
                if (target <= nums[mid] && target >= nums[0])
                    // 此时target的值处于nums[0]和nums[mid]中，故可能在[l, mid]中。
                    r = mid;
            } else { // mid在数组后半部分
                if (target >= nums[0])
                    // 可以推出target的值一定大于nums[mid]，target只可能在[l, mid]中。
                    r = mid;
                if (target <= nums[mid])
                    // 可以推出target的值一定小于nums[0]，target只可能在[l, mid]中。
                    r = mid;
                if (target > nums[mid] && target < nums[0])
                    // 此时target的值处于nums[0]和nums[mid]中，故可能在[mid+1, r]中。
                    l = mid + 1;
            }
        }
        return nums[l] == target ? l : -1;
    }
}

参考链接：

• https://www.acwing.com/solution/LeetCode/content/104/