漫画:什么是 “哈夫曼树” ?
![]()
作者 | 小灰
来源 | 程序员小灰(ID:chengxuyuanxiaohui)
————— 第二天 —————
————————————
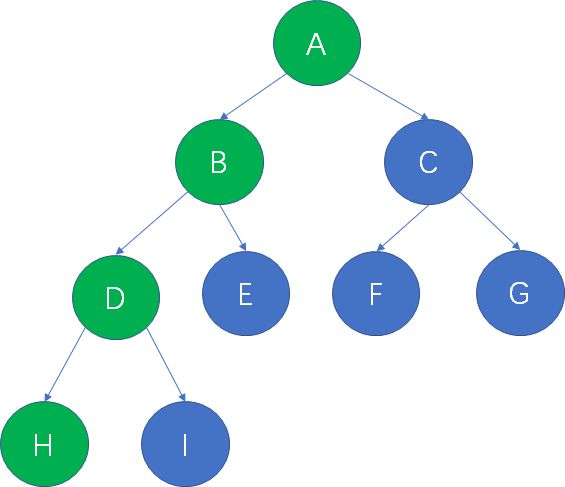
概念1:什么是路径?
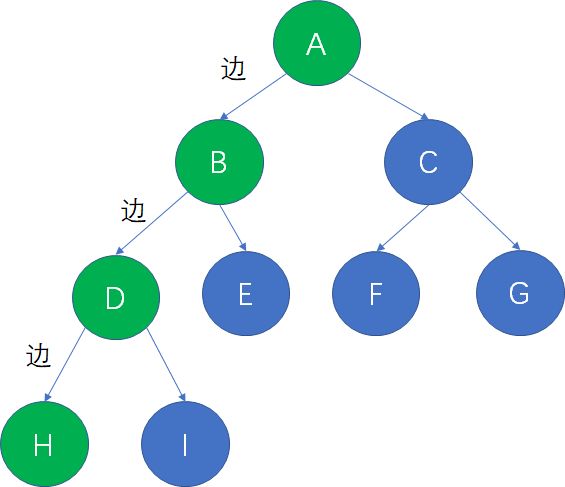
在一棵树中,从一个结点到另一个结点所经过的所有结点,被我们称为两个结点之间的路径。
上面的二叉树当中,从根结点A到叶子结点H的路径,就是A,B,D,H。
概念2:什么是路径长度?
在一棵树中,从一个结点到另一个结点所经过的“边”的数量,被我们称为两个结点之间的路径长度。
仍然用刚才的二叉树举例子,从根结点A到叶子结点H,共经过了3条边,因此路径长度是3。
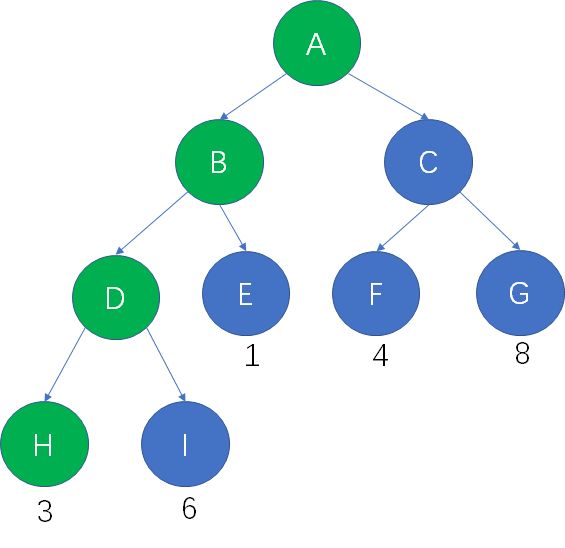
概念3:什么是结点的带权路径长度?
树的每一个结点,都可以拥有自己的“权重”(Weight),权重在不同的算法当中可以起到不同的作用。
结点的带权路径长度,是指树的根结点到该结点的路径长度,和该结点权重的乘积。
假设结点H的权重是3,从根结点到结点H的路径长度也是3,因此结点H的带权路径长度是 3 X 3 = 9。
概念4:什么是树的带权路径长度?
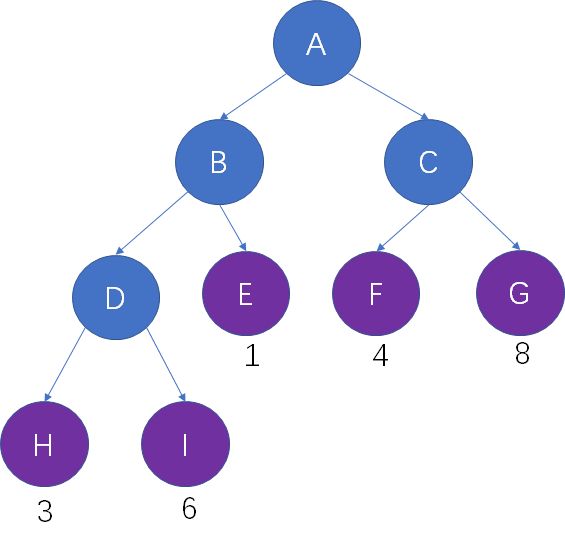
在一棵树中,所有叶子结点的带权路径长度之和,被称为树的带权路径长度,也被简称为WPL。
仍然以这颗二叉树为例,树的路径长度是 3X3 + 6X3 + 1X2 + 4X2 + 8X2 = 53。
哈夫曼树是由麻省理工学院的哈夫曼博士于1952年发明,这到底是一颗什么样的树呢?
刚才我们学习了树的带权路径长度(WPL),而哈夫曼树(Huffman Tree)是在叶子结点和权重确定的情况下,带权路径长度最小的二叉树,也被称为最优二叉树。
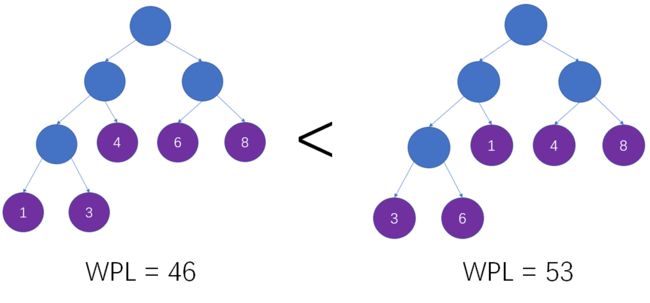
举个例子,给定权重分别为1,3,4,6,8的叶子结点,我们应当构建怎样的二叉树,才能保证其带权路径长度最小?
原则上,我们应该让权重小的叶子结点远离树根,权重大的叶子结点靠近树根。
下图左侧的这棵树就是一颗哈夫曼树,它的WPL是46,小于之前例子当中的53:
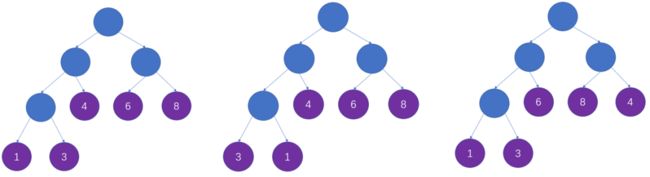
需要注意的是,同样叶子结点所构成的哈夫曼树可能不止一颗,下面这几棵树都是哈夫曼树:
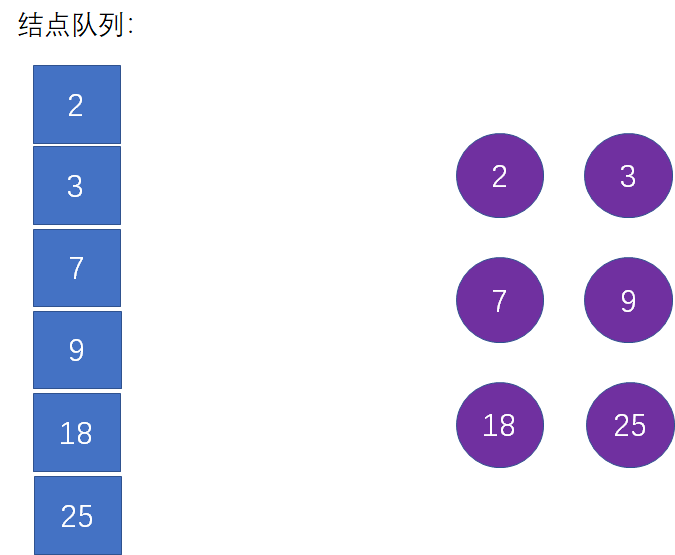
假设有6个叶子结点,权重依次是2,3,7,9,18,25,如何构建一颗哈夫曼树,也就是带权路径长度最小的树呢?
第一步:构建森林
我们把每一个叶子结点,都当做树一颗独立的树(只有根结点的树),这样就形成了一个森林:
在上图当中,右侧是叶子结点的森林,左侧是一个辅助队列,按照权值从小到大存储了所有叶子结点。至于辅助队列的作用,我们后续将会看到。
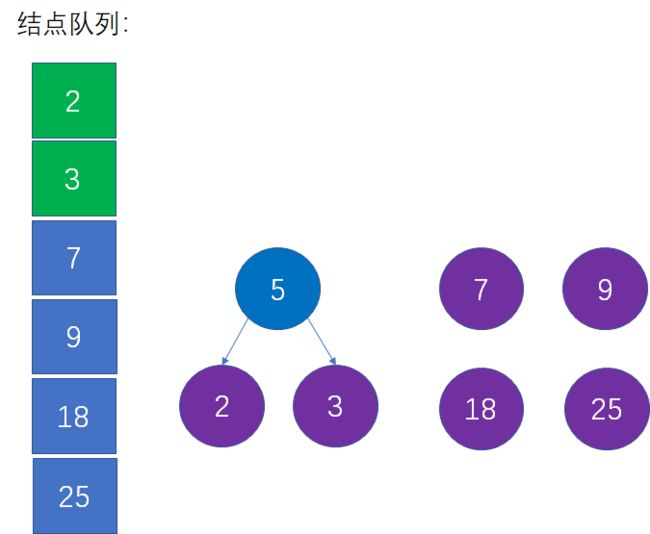
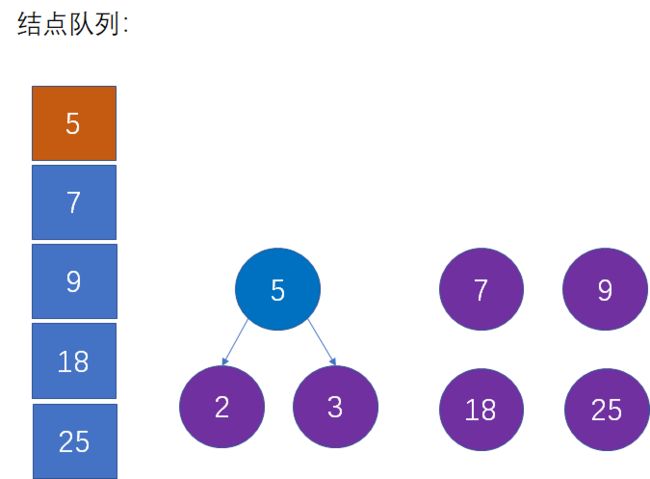
第二步:选择当前权值最小的两个结点,生成新的父结点
借助辅助队列,我们可以找到权值最小的结点2和3,并根据这两个结点生成一个新的父结点,父节点的权值是这两个结点权值之和:
第三步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列
也就是从队列中删除2和3,插入5,并且仍然保持队列的升序:
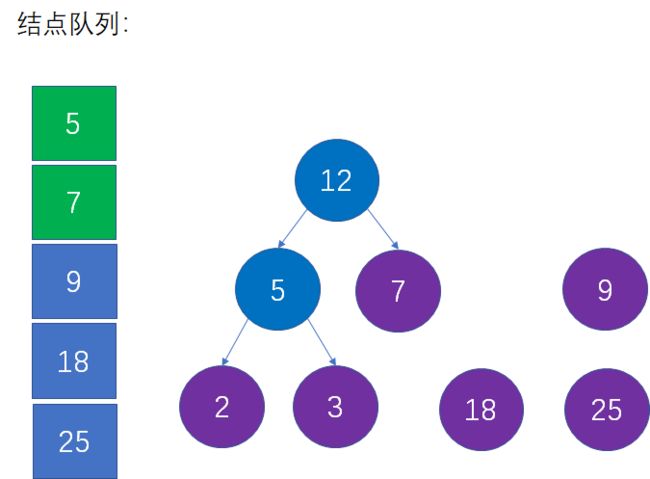
第四步:选择当前权值最小的两个结点,生成新的父结点。
这是对第二步的重复操作。当前队列中权值最小的结点是5和7,生成新的父结点权值是5+7=12:
第五步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列。
这是对第三步的重复操作,也就是从队列中删除5和7,插入12,并且仍然保持队列的升序:
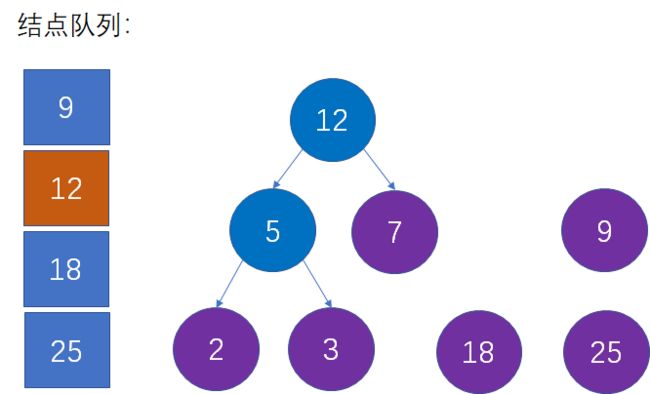
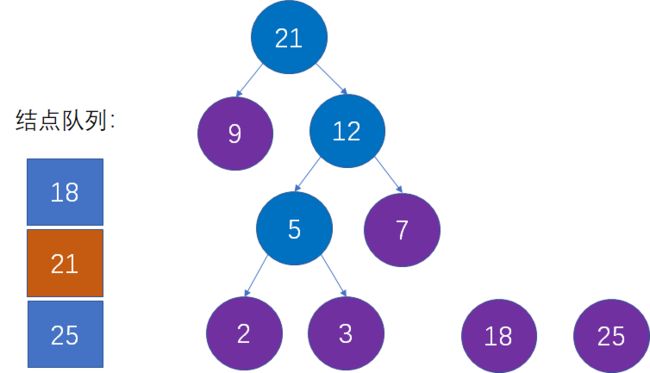
第六步:选择当前权值最小的两个结点,生成新的父结点。
这是对第二步的重复操作。当前队列中权值最小的结点是9和12,生成新的父结点权值是9+12=21:
第七步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列。
这是对第三步的重复操作,也就是从队列中删除9和12,插入21,并且仍然保持队列的升序:
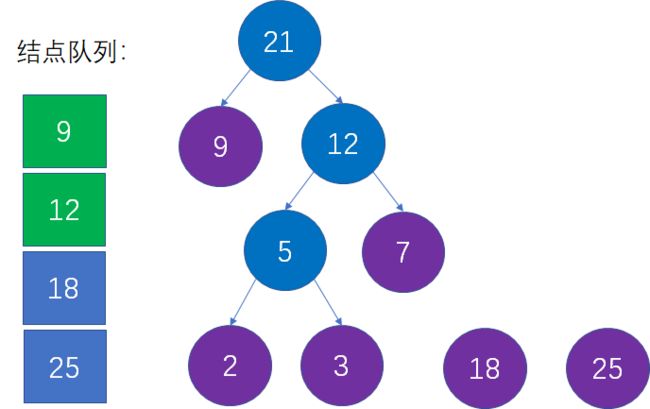
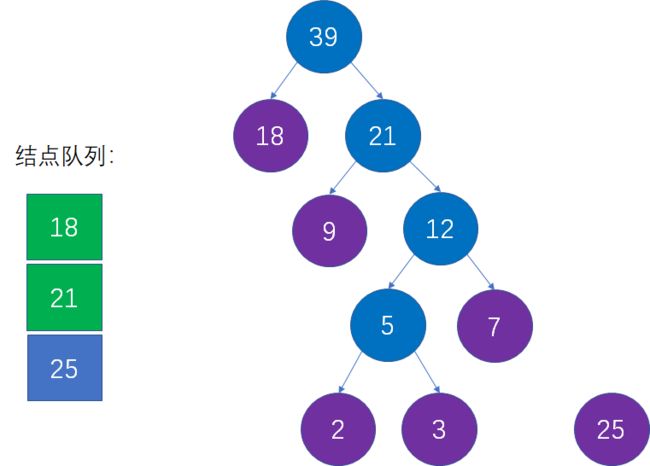
第八步:选择当前权值最小的两个结点,生成新的父结点。
这是对第二步的重复操作。当前队列中权值最小的结点是18和21,生成新的父结点权值是18+21=39:
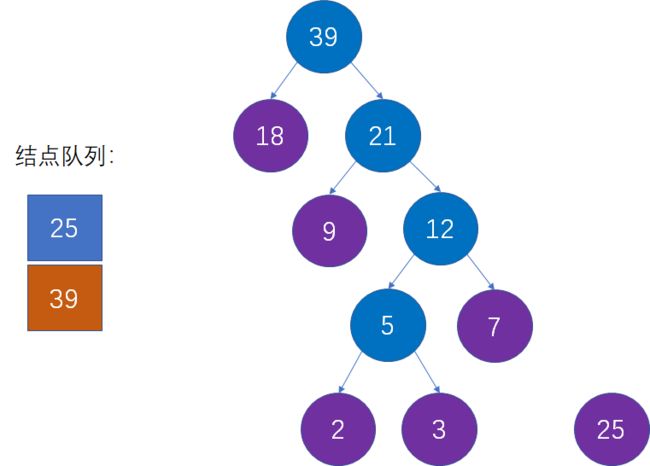
第九步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列。
这是对第三步的重复操作,也就是从队列中删除18和21,插入39,并且仍然保持队列的升序:
第十步:选择当前权值最小的两个结点,生成新的父结点。
这是对第二步的重复操作。当前队列中权值最小的结点是25和39,生成新的父结点权值是25+39=64:
第十一步:从队列中移除上一步选择的两个最小结点,把新的父节点加入队列
这是对第三步的重复操作,也就是从队列中删除25和39,插入64:
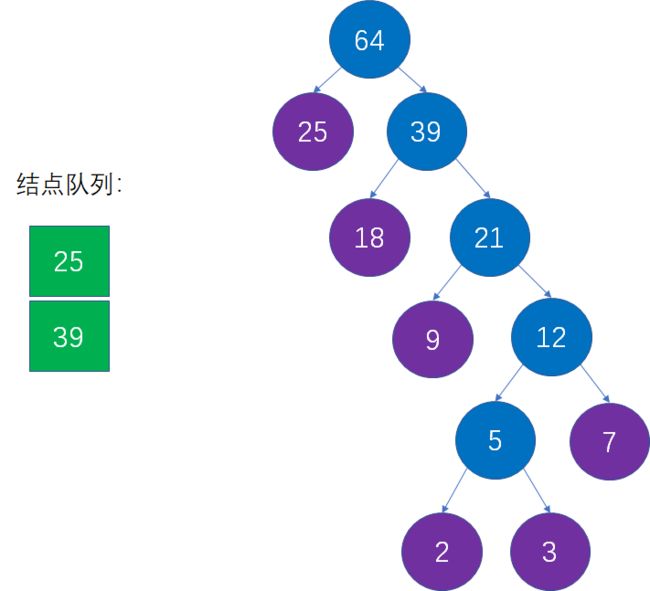
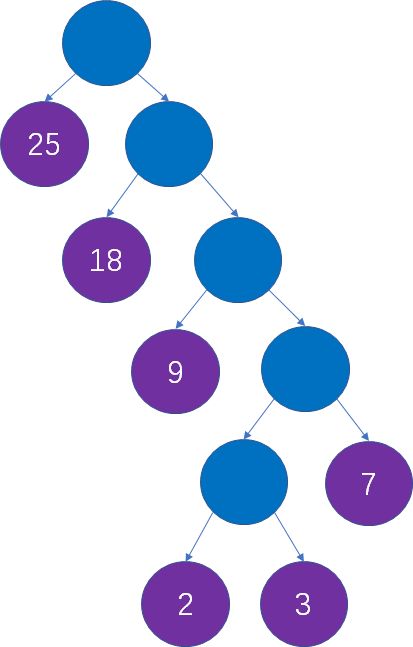
此时,队列中仅有一个结点,说明整个森林已经合并成了一颗树,而这棵树就是我们想要的哈夫曼树:
private Node root;
private Node[] nodes;
//构建哈夫曼树
public void createHuffman(int[] weights) {
//优先队列,用于辅助构建哈夫曼树
Queue nodeQueue = new PriorityQueue<>();
nodes = new Node[weights.length];
//构建森林,初始化nodes数组
for(int i=0; i 1) {
//从结点队列选择权值最小的两个结点
Node left = nodeQueue.poll();
Node right = nodeQueue.poll();
//创建新结点作为两结点的父节点
Node parent = new Node(left.weight + right.weight, left, right);
nodeQueue.add(parent);
}
root = nodeQueue.poll();
}
//按照前序遍历输出
public void output(Node head) {
if(head == null){
return;
}
System.out.println(head.weight);
output(head.lChild);
output(head.rChild);
}
public static class Node implements Comparable{
int weight;
Node lChild;
Node rChild;
public Node(int weight) {
this.weight = weight;
}
public Node(int weight, Node lChild, Node rChild) {
this.weight = weight;
this.lChild = lChild;
this.rChild = rChild;
}
@Override
public int compareTo(Node o) {
return new Integer(this.weight).compareTo(new Integer(o.weight));
}
}
public static void main(String[] args) {
int[] weights = {2,3,7,9,18,25};
HuffmanTree huffmanTree = new HuffmanTree();
huffmanTree.createHuffman(weights);
huffmanTree.output(huffmanTree.root);
}
在这段代码中,为了保证结点队列当中的结点始终按照权值升序排列,我们使用了优先队列PriorityQueue。
与此同时,静态内部类Node需要实现比较接口,重写compareTo方法,以保证Node对象在进入队列时按照权值来比较。
【END】
![]()
更多精彩推荐
☞曾遭周鸿祎全网封杀的 360 猛将 :草根打工到 36 岁身家上亿的逆袭!
☞2020 年,网络安全方面 5 大值得学习的编程语言
☞10 倍高清不花!大麦端选座 SVG 渲染
☞微软为一人收购一公司?破解索尼程序、写黑客小说,看他彪悍的程序人生!
机器学习项目模板:ML项目的6个基本步骤
☞IBM、微软、苹果、谷歌、三星……这些区块链中的科技巨头原来已经做了这么多事!
资深程序员总结:分析Linux进程的6个方法,我全都告诉你
今日福利:评论区留言入选,可获得价值299元的「2020 AI开发者万人大会」在线直播门票一张。 快来动动手指,写下你想说的话吧。
![]() 点击阅读原文,精彩继续!
点击阅读原文,精彩继续!
你点的每个“在看”,我都认真当成了喜欢