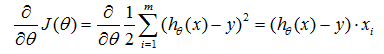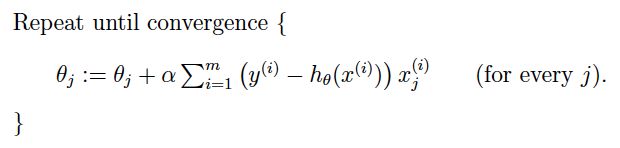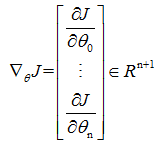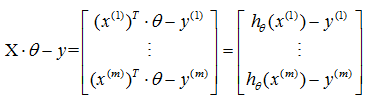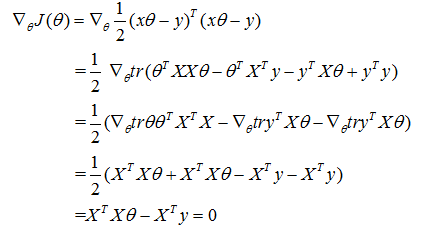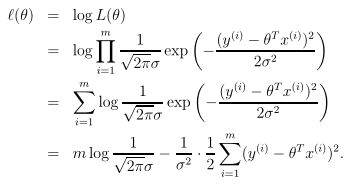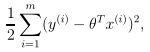一、机器学习概述:
1. 学习动机:
- 机器学习已经在不知不觉中渗透到人们生产和生活中的各个领域,如邮箱自动过滤的垃圾邮件、搜索引擎对链接的智能排序、产品广告的个性化推荐等;
- 机器学习横跨计算机科学、工程技术和统计学等多个学科,需要融合多学科的专业只是,也同样可以作为实际工具应用到各行各业之中;
- 如何从移动计算和传感器所产生的海量数据中抽取出有价值的信息将成为一个非常重要的课题,也会是未来生产力的爆发点。
2. 定义:
- Authur Samuel在1959年非正式地定义机器学习为:在不直接针对问题进行编程的情况下赋予计算机学习学习能力的一个研究领域;他曾经写过一个让计算机自己和自己下西洋棋的算法,通过成千上万次练习,程序开始明白怎样的局面会有利于赢,怎样的局面会导致于输。
- Tom Mitchell在1998年提出更为正式的机器学习定义:一个合适的学习问题——对于一个计算机程序来说给它一个任务T和一个性能测量方法P,如果在经验E的影响下,P对T的测量结果得到了改进,那么就说该程序从E中学习。(例如,T为下棋,E为下棋的经验,P为它与人类棋手对弈的胜率,这样定义该程序在学习怎样下棋)
3. 组成部分:
- Supervised Learning(监督学习):人工地给算法提供了标准答案,如Regression(回归):需要预测的变量是连续的,根据房屋面积与价格之间的已知关系来判断新的房屋面积所对应的价格;Classification(分类)根据肿瘤的大小来判断病人是否患有癌症。
- Learning Theory(学习理论):能够理解和保证学习型算法高效地工作,如读取邮编号码中所用到的数学理论基础。
- Unsupervised Learning(非监督学习):不知道任何数据标准答案,寻找数据中的结构,如鸡尾酒问题中用到的聚类算法。
- Reinforcement Learning(强化学习):不需要作出一次性决策的情况下,在一段时间内做出一系列的决策,如教会小车在告诉行驶中如何避开障碍。
二、监督学习应用:
- 线性回归
- 梯度下降
- 标准方程
- 概率解释
1. 线性回归
引例:房屋估价系统
房屋估价系统问题就是当知道房屋面积、卧室个数与房屋价格的对应关系之后,在得知一个新的房屋信息后如何得到对应的新房屋价格,这类问题可以简化为:
寻找房屋面积、卧室个数与房屋价格之间关系方程的过程就是回归,这里假设他们之间是线性关系,即房屋价格可以被表示为房屋面积与卧室个数的一维线性方程,如:
![]()
这里x表示与房屋价格相关的特征,x1为房屋面积,x2为卧室个数,θ可以理解为各个特征的影响权重。
抽象地总结一下
回归:用一条曲线对数据点进行拟合,该曲线称为最佳拟合曲线,这个拟合过程叫做回归。回归问题的求解过程就是通过训练分类器采用最优化算法来寻找最佳拟合参数集。
线性回归:当该曲线为一条直线时,就是线性回归。其中,“线性”是指特征和结果都是线性的,即不大于一次方,每个分量表示一个特征,向量表示为:
![]()
h=hypothesis,是特征函数的估计表达式,由于求解一个含有参数众多的线性矩阵方程,需要建立足够的约束条件才能得到唯一解。
实际上由于条件有限,大多数情况下都是求解超定方程组的近似最优解,即满足使得估计值与实际值的方差最小时的参数解,可以表示为:
这就是损失函数,求解的方法有最小二乘法、梯度下降法等。
线性损失函数的求解方法:
- 最小二乘法,求误差的最小平方和,非线性最小二乘法无闭式解,一般通过迭代法求解;而线性最小二乘有闭式解,通过一系列的数学推导,可以得到一个标准方程:
- 梯度下降法,利用沿着梯度下降最快的方向求偏导数,得到损失函数的全局最小值时的参数θ,涉及到偏导数、学习速度、更新、收敛等问题。
非线性最小二乘法的求解方法:
- 高斯牛顿法,常用于求解非线性最小二乘的迭代法,可视为标准非线性最小二乘求解方法。
- Levenberg-Marquardt迭代法,求解非线性最小二乘问题,结合了梯度下降和高斯-牛顿法。
2. 梯度下降法
- 梯度下降法的思想:
1)首先对θ赋值,这个值可以是随机的,也可以是一个零向量;
2)改变θ的值,使得J(θ)按梯度下降的方向进行减少;
3)当J(θ)下降到无法下降时为止,即J(θ)对θ的导数为0时,比较J(θ)的值是否有变化。
对损失函数J(θ)求偏导,得到:
- 参数更新过程:
更新过程可以理解成:θi沿着梯度下降最快的方向进行递减的过程。
左边的θi表示更新之前的值,等式右边表示沿着梯度方向减少的量,α表示步长,也称作学习速度,这个值需要人工手动设置。
不断更新θi的值直到J(θ)收敛,可以通过比较J(θ)的前后两个值是否有发生变化(继续下降),当没有发生变化时表示已经达到了最小值(可能是局部最小值)。
- 参数设置问题:
初始值和学习速度都是是人工设置的,而梯度下降法对这些参数又是敏感的。
初始值的设置会影响到最终J(θ)的最小值,它可能是局部最小值,也可能是全局最小值。
学习速度的设置也会影响到梯度下降的性能和结果:
1)当设置过小时,由于沿着最陡峭方向每次迈进的步伐太小,而导致收敛时间过长;
2)当设置过大时,很有可能会直接越过最小值,而无法得到J(θ)的最小值。
- 梯度下降法的改进:
上述梯度下降法也叫批量梯度下降法(Batch gradient descent),每次迭代都需要用到训练集所有的数据,收敛速度较慢。
因此,得到它的改进算法随机梯度下降法(Stochastic gradient descent),也叫增量梯度下降法(Incremental gradient descent)。
随机梯度下降通过每个样本来迭代更新一次参数,可能未遍历整个样本就已经找到最优解,大大提高了算法的收敛速度。
最小化每个样本的损失函数,虽然每次迭代结果不一定都是全局最优解,却总是沿着这个方向发展,故最终结果总是接近全局最优解。
3. 标准方程
在清楚了线性回归模型(Model)、损失函数和最小二乘法(Strategy)和梯度下降法(Algorithm)之后,顺理成章地想知道方程的解。
首先,需要回顾五个定理:
![]()
![]()
![]()
![]()
![]()
然后,就可以利用这五个定理来推导线性最小二乘法的闭式解,即标准方程。
(1)向量表示
利用梯度符号将损失函数梯度的向量表示:
估计值与真实值之间的差的向量表示:
损失函数的向量表示:
(2)设置损失函数的梯度为0
可以得到标准方程:
4. 概率解释
除了上面标准方程中可以采用向量解释最小二乘法,它也具有概率意义。
假设输入特征与输出结果之间的表达式为:
其中,最后一项是误差项,可以表示未捕捉到的特征或随机噪声,它服从标准正态分布且是IID的,即:
给定了参数θ和特征矩阵X时y的似然函数L(θ)为:
![]()
它其实是一个θ的函数,为了求解最大似然,通常取其log构成log likelihood:
求解l(θ)的最大似然估计后,得到的结果与梯度下降法求解最小值J(θ)是相同的。
基本概念可以参考:
对线性回归、逻辑回归、各种回归的概念学习
机器学习中的数学(1)-回归(regression)、梯度下降(gradient descent)
梯度下降法(一)入门