| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程/ | 2020年春季计算机学院软件工程(罗杰 任健) |
| 这个作业的要求在哪里? | 个人项目作业 |
| 教学班级 | 006 |
| 项目GitHub地址 | Line |
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 20 | 20 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 30 | 30 |
| · Design Spec | · 生成设计文档 | 20 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 5 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| · Design | · 具体设计 | 60 | 60 |
| · Coding | · 具体编码 | 120 | 120 |
| · Code Review | · 代码复审 | 30 | 30 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 120 | 360 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 30 | 20 |
| · Size Measurement | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 30 |
| 合计 | 490 | 725 |
解题思路
基础部分
直线可表示为 y = kx + b, 当直线垂直于x轴时(k不存在),要进行区别讨论。其中的k,b都可以通过分数的形式表示,经过换件多项式可以得出,两直线的交点可以使用分数表示,这样完全不会丢失精度。
通过多项式计算可以用分数表示各个交点,这样不用算除法也不会丢失精度。
可以使用pair
其中,当k不存在时,pair的first(分母)为0,这时候就要分情况讨论,不能直接带入公式。
互相平行的线没有交点,不存在互相重叠的直线(根据题意可得)。
附加题
涉及到二次方程求解,无法继续使用分数,于是将分数转化为float精度的小数进行计算。
直线与直线相交,同基础题。
圆与圆相交,求出两圆的公共弦,转化为线与圆相交。需注意圆与圆之间的位置关系(相离相切相交)
直线与圆相交,没有捷径可以走。老老实实带入方程求解。需要注意的是判断直线与圆有没有交点、有几个交点。
设计过程
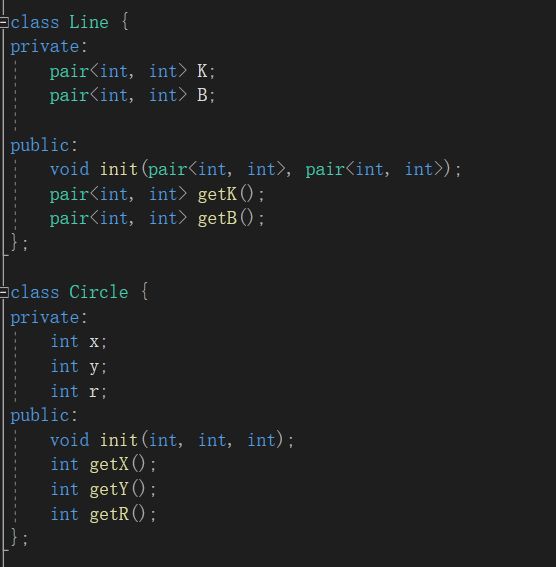
设计了两个类Line和Circle
Line中的K和B表示y = kx + b 中的参数。用pair
Circle中三个参数分别为圆心坐标和圆的半径。
基本思想为:将Line和Circle存进两个vector容器中,循环比较求出交点。再查找容器PointList,若此交点不在其中,则加入。
设计了三个函数来求交点:
Line_intersection() ;求线与线之间的交点
Circle_intersection();求圆与圆之间的交点
CirLine _intersection();求直线与圆之间的交点
详细代码说明在下面。
再基础作业部分使用分数来进行计算,附加题部分涉及到开根,没办法进行分数表示。但为了不丢失基础部分的精度,故在进行圆的计算时将直线部分的分数转化为了浮点小数以便于计算。
由于时间问题,没有过多考虑小数带了的精度丢失。
代码说明
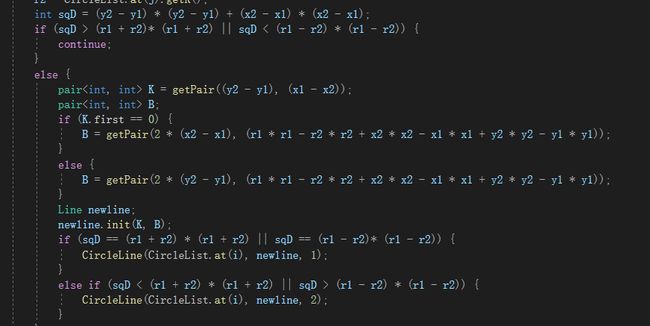
直线与直线相交
其中特判了k分母为0的情况
圆与圆相交
转换为直线与圆相交之前要判断两圆之间的位置关系
直线与圆相交
如下,带入公式求解。
Code Quality Analysis
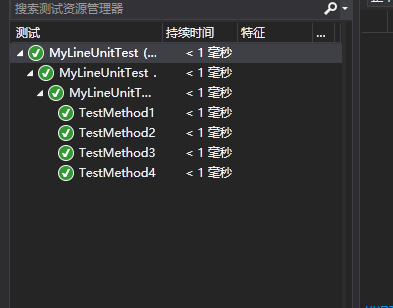
单元测试
代码覆盖率测试
我使用了opencppcover插件来进行覆盖率测试,调试了好几天也没能解决无法运行了问题。期间还下载了vs企业版,但仍不能成功运行代码覆盖率测试。这样导致我没法进行性能测试,这是个教训。