任意多边形的三角剖分可视化实现（先划分成单调多边形，再在单调多边形中做三角剖分）

多边形三角剖分是计算几何中的经典问题，起源于一个有趣的艺术画廊问题。目前有很多不同的算法实现了对多边形的三角剖分，三角化算法所追求的目标主要有两个：形状匀称和计算速度快，这也决定了多边形三角剖分的两个不同的应用方向。在形状匀称方面，人们对三角化的性质、 形状最优准则及算法进行了深入研究 ，采用较多的是 Delaunay 准则。这些算法在保证形状匀称的前提下，也尽可能考虑了提高计算速度。在有限元分析等许多应用场合三角形匀称是必须的，对单元质量是有一定要求的。但有些应用场合对三角形匀称性的要求不高，甚至没有匀称性要求。例如用 OpenGL显示图形时，不同的三角化策略对图形效果基本没有影响。在三角化时考虑匀称性，会使算法思想受到限制，从而影响算法效率。因此追求较高计算效率的三角化算法还是有意义的。这里我们使用时间复杂度为O(n log n)的多边形三角剖分算法，在学堂在线邓俊辉老师的计算几何课中用的就是这个方法。

此算法的核心思想是首先对多边形进行单调划分，也就是将多边形分解为若干个单调多边形，然后再对单调多边形进行三角剖分，最终生成对初始多边形的三角剖分。

单调多边形的划分：

什么是单调多边形？

一个简单多边形关于某条直线L单调（monotone with respect to a line L），如果对任何一条垂直于L的直线L’，L’与多边形的交都是连通的，即它们的交可能是一条线段，或者一个点，也可能是空集。在这里我们就让y轴做L，x轴做L’。

如何划分单调多边形？

我们采用扫描线的策略，将顶点按照y坐标升序排列放入事件队列，每次扫描线都是在顶点所在的与x轴平行的直线上。

首先我们要考虑什么时候要进行划分，由定义可以知道，当一条扫描线不能连续的穿过多边形时，我们就需要做一些必要的切割。可以看下面的例子体会：

可以看到无非就两种情况可能导致一条扫描线不能连续的穿过多边形：

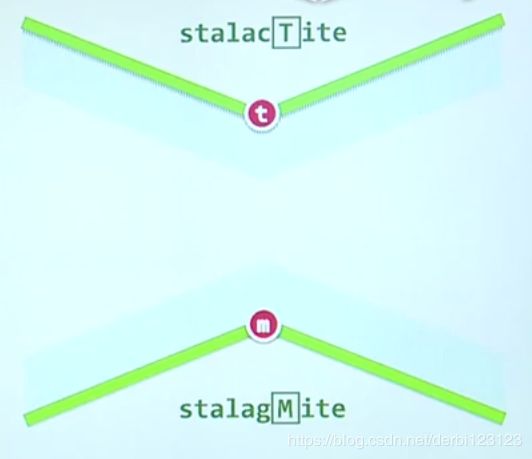
他们的英文也恰到好处，很形象，stalagmite是石笋，而stalactite是钟乳石，当直线穿过他们时，显然会被分割从而导致不连续，而我们可以敏锐的观察到所有的t点的y坐标都大于它两个邻接点的y坐标，所有的m点的y坐标都小于它两个邻接点的y坐标，并且石笋只能从地里长出来，钟乳石则是从洞顶向下凸出来，因为我们一开始就是对顶点按照y坐标排序的，所以很容易的可以把多边形划分成上下两部分，分别去找这些钟乳石和石笋。

并且我们只需要连接钟乳石/石笋和它们的上一个扫描过的顶点即可完成划分。

事情就是这么简单且形象。下面是专门用来划分成单调多边形的效果及代码：

#include 
#include 
#include 
#include 
#include 
#include 
#define Width 400
#define Height 300
#define PointNum 10
using namespace std;

struct Point{
	int x,y;
	int index;//记录最初的顶点编号
	//在顶点事件的优先队列中，按y升序排列，y相同则x小的在前
	friend bool operator < (const Point &p1,const Point &p2)
	{
			return p1.y != p2.y ? p1.y > p2.y : p1.x > p2.x ;
	}
};
vector<Point> points;
priority_queue<Point> VertexEvent;
//初始化顶点事件队列和多边形
void initVertexs(int P[])
{
	int index=0;
	for(int i=0;i<PointNum*2;i+=2){
		setcolor(RGB(255,255,255));
		setfillcolor(RGB(255,255,255));
		fillcircle(P[i],P[i+1],3);
		Point point;
		point.x=P[i];
		point.y=P[i+1];
		point.index=index;
		index++;
		points.push_back(point);
		VertexEvent.push(point);
	}
	setcolor(RGB(255,255,255));
	polygon((POINT*)P, PointNum);
}
//遍历顶点事件队列划分单调多边形
void Monotone_Decomposition()
{
	Point PreTmp,next;//队列中前一个顶点和后一个顶点
	while(!VertexEvent.empty()){
		Point tmp=VertexEvent.top();
		int pre,succ;//两个相邻节点的编号
		if(tmp.index==0){
			pre=PointNum-tmp.index-1;
			succ=tmp.index+1;
		}else if(tmp.index==PointNum-1){
			pre=tmp.index-1;
			succ=0;
		}else{
			pre=tmp.index-1;
			succ=tmp.index+1;
		}
		if(VertexEvent.size()>((int)PointNum/2)){//上半部分
			PreTmp=tmp;
			VertexEvent.pop();
			next=VertexEvent.top();
			//如果当前顶点的y值比相邻两顶点的y值小
			if(tmp.y>points[pre].y&&tmp.y>points[succ].y){
				setcolor(RGB(0,0,255));
				line(tmp.x,tmp.y,next.x,next.y);
			}
		}else{//下半部分
			if(tmp.y<points[pre].y&&tmp.y<points[succ].y){//如果当前顶点的y值比相邻两顶点的y值大
				setcolor(RGB(0,0,255));
				line(tmp.x,tmp.y,PreTmp.x,PreTmp.y);
			}
			VertexEvent.pop();
		}
		PreTmp=tmp;
	}
}
int main()
{
	initgraph(Width,Height);
	int P[]={150,20,200,60,180,80,300,40,350,230,300,120,250,260,200,180,120,290,60,100};
	initVertexs(P);//初始化顶点事件队列和多边形
	Monotone_Decomposition();
	getch();
	closegraph();
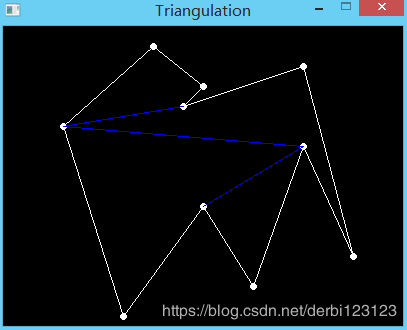
	return 0;
}

那如何得到划分后的数个单独的单调多边形呢？

对于钟乳石、石笋以及分割点（上一个扫描线所在的点），它们参与构造不止一个单调多边形。我们恰好可以从上面这个效果中看到构成单调多边形的其他点恰好位于钟乳石、石笋以及分割点之间（在代码中我们有相应的编号），并且这种顺序恰好是逆时针的（因为我们的顶点集合中顶点就是按顺时针构造的）。所以我们只要在每次分割单调多边形时记录对应的分割线的端点即可（注意，对于钟乳石和石笋以及这二者和分割点的分割线操作可能不同）

在单调多边形中做三角剖分

现在已经是单调的了，所以我们只需要自顶向下扫描所有单调多边形，我们用栈存那些已经扫描过却不能和之前扫描过的点构成三角形的点（也就是相邻三点是凹的），比如下面这个例子：

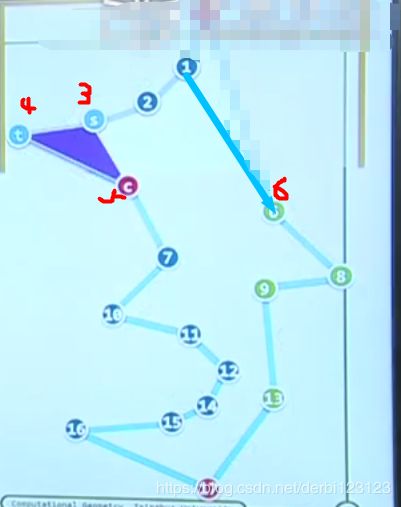
当我们自顶向下扫描过三号点（S）时，我们并不能构造1、2、3的三角形，正因为他们的内角的凹的，所以3、4都会入栈，而到了5号点（C）时，显然我们再去从栈中取元素检测时，C可以一直构造相邻三个点的三角形直到1号点，此时，2、3、4已经依次出栈，而1和5应给留下来做后面的判断。依次进行下去即可。

//单调多边形的三角剖分
void Triangulating_Monotone_Polygons(Monotone_Polygon monotone)
{
	stack<Point> WaitPoint;//暂时不知道归属的顶点栈
	//初始化为前两个顶点
	WaitPoint.push(monotone.Polygon.top());
	monotone.Polygon.pop();
	WaitPoint.push(monotone.Polygon.top());
	monotone.Polygon.pop();
	while(!monotone.Polygon.empty()){//应该剩下最后一个元素
		Point tmp=monotone.Polygon.top();
		while(WaitPoint.size()>1){//有可能不止检测1次
			Point first=WaitPoint.top();
			WaitPoint.pop();
			Point second=WaitPoint.top();
			WaitPoint.pop();
			//下一个元素C不是与栈顶相连就是与栈底相连
			if(tmp.index==first.index+1){
				if(ToLeft(second,first,tmp)){//不是凹的
					setcolor(RGB(0,255,0));
					line(tmp.x,tmp.y,second.x,second.y);
					//然后次栈顶元素就可以解放了，原来的栈顶变成次栈顶，新元素变成栈顶
					WaitPoint.push(second);
				}else{//如果无法构成三角形还要进入栈中等待
					WaitPoint.push(second);
					WaitPoint.push(first);
					WaitPoint.push(tmp);
					break;
				}
			}else{
				setcolor(RGB(0,255,0));
				line(tmp.x,tmp.y,second.x,second.y);
				WaitPoint.push(second);
			}
			
		}
		WaitPoint.push(tmp);
		monotone.Polygon.pop();
	}
}