双目立体匹配算法：SGM

一、简介

  立体匹配旨在为校正后的左右视图提供稠密的匹配对，这种问题称为"stereo correspondence problem"。有大量的算法用于求解立体匹配问题，根据Scharstein和 Szeliski的研究，所有这些算法的计算流程基本上都可以分为四个步骤：A.匹配代价计算；B.代价聚合； C.视差计算/优化； D.视差细化。其中匹配代价用来度量像素或者像素块之间的相似性，计算匹配代价的方法有AD、SAD、BT、NCC、Census-Hamming、HMI、Daisy以及基于深度学习方法的匹配代价等等。代价聚合的目的是将每个像素的匹配代价和它周围的像素关联起来，常用的方法是将一个固定尺寸的窗口中的相同视差下的匹配代价简单求和、加权求和，或者在利用图像中的梯度或颜色进行分割后的区域中进行聚合，还有一些方法使用引导滤波等进行代价聚合。
  在上述框架下，立体匹配算法基本被分类为两种：（1）局部算法：A => B => C => D（2）全局算法：A => C => D。局部算法一般在代价聚合之后，通过选择最低匹配代价来得到对应的视差，即winner takes all。全局算法没有进行代价聚合，而是定义了一个包含数据项和平滑项的能量函数并通过最小化能量函数来求得视差，数据项一般为所有像素的代价和，平滑项一般为对邻域像素视差差异的惩罚，部分方法还添加更多的项，比如对遮挡区域的惩罚、左右一致性或对称性约束，或者根据分割区域对平滑项进行加权等。根据所使用的优化方法，全局算法主要有Dynamic programming、Graph Cut、Belief Propogation等。

​  全局算法由于非常高的运算量或内存消耗，在大多数场合都无法应用，而局部算法虽然速度很快，但是鲁棒性差，匹配质量比较低。2005年，Heiko Hirschmuller提出了一种半全局的立体匹配算法，叫做SGM，该算法建议采用单像素互信息(HMI)作为匹配代价，沿着多个方向进行一维能量最小化来近似替代二维全局能量最小化，因此被称为半全局算法。SGM的运算速度远远快于大多数全局算法，同时精度也比较高，除了深度学习的方法外，SGM在各种公开数据集的双目匹配任务的排行榜上一直都位列前排，证明了SGM算法的强大。在OpenCV中高度优化的SGBM算法对于1920*1080分辨率的图像，其运行时间可以低至300ms以内（当然这还取决于机器性能）。

二、SGM

1.pixelwise匹配代价计算：HMI

​  互信息(Mutual Information)用于表征两幅图像共有信息量的大小，可作为两幅图像相似性的度量，然而MI是针对整张图像而言的，Junhwan Kim通过对MI进行泰勒展开得到单像素的互信息HMI的计算方法，该方法作为像素相似性度量对光照变化较为鲁棒，是一种优秀的代价函数。关于如何求解单像素互信息，限于篇幅这里就不叙述了，详情可以查看作者论文。

2.动态规划

2.1一些基本概念

  动态规划(dynamic programming)是一种求解多阶段决策过程(decision process)最优化的数学方法，即利用各阶段之间的关系，逐个求解。下面介绍一些动态规划算法的基本概念。
（1）阶段：阶段是整个过程的自然划分，通常按时间顺序或空间特征划分阶段，表示阶段序号的变量称为阶段变觉，一般用字母$k$表示。
（2）状态：在整个过程中，每个阶段开始所处的自然状况或客观条件称为状态，是不可控因素。状态变量常用$s_k$表示。
（3）决策：一个阶段的状态确定后，可以作出不同的选择，从而演变到下一阶段的某个状态，这种选择叫做决策，常用$u_k$表示。
（4）策略：由决策组成的序列称为策略。
（5）状态转移方程：给定第k阶段的状态和决策，则第$k+1$阶段的状态由状态转移方程决定。
（6）指标函数：指标函数是衡量过程优劣的数量指标，它是定义在全过程和所有后部子过程上的数量函数，对于给定的状态，指标函数值 随策略改变，采用不同的策略可以得出不同的指标函数值。
（7）最优策略和最优轨线：使指标函数达到最优值(最大值或最小值)的策略称为最优策略，按最优策略和状态转移方程得出的状态序列为最优轨线。

2.2基于动态规划的立体匹配

  动态规划立体匹配是建立在极线约束的基础上的，其大致思想就是在每条对极线上寻找最优路径，使得能量函数在每条对极线上达到最低。经过立体校正以后，对极线对应的则是图像中的每一行。

在沿着对极线进行动态规划时通常要遵循以下几个约束：
 (1) 视差范围约束：即视差的搜索范围是有限的，不能在一个无限大的区间内去搜索视差；
 (2) 唯一性约束：给定左图中的一个像素点，它在右图中最多只能有一个对应点；
 (3) 可见性约束：当某点处于遮挡区域时，它在另一幅图中将无法找到对应点，遮挡区域一般出现在由背景进入前景或者由前景进入背景的边界地带；
 (4) 顺序性约束：假如在左图中的两个点的横坐标为$x1,x2$，在右图中的对应点横坐标为$y1,y2$，若$x1<x2$，则$y1<y2$；
 (5) 连续性约束或平滑性约束：由于现实世界物体是连续的，因此在图像中的视差也应当是均匀平滑变化的，但是在物体的边缘处视差是有可能发生大的跳变。

动态规划算法一般分为以下几个步骤：

(1) 阶段划分

  由于通过极线校正的图像只在水平方向寻找扫描点，所以算法是在水平扫描线的视差空间切面上寻找最优路径的过程，如下图 所示，以像素点的行方向为横坐标，视差值d 为纵坐标，依次将整个过程分为 1、2、3、…、k 共k个阶段。

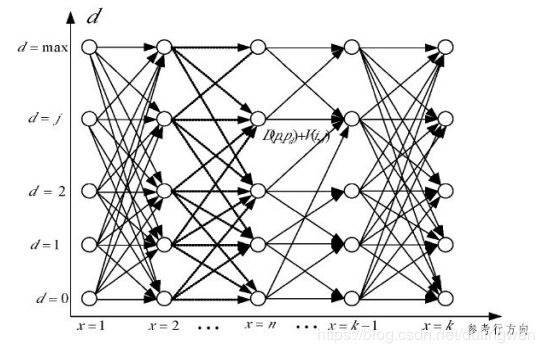
(2) 确定状态

  将上述各个阶段所处的匹配阶段用不同的状态表示。如下图所示，每一个阶段的状态就是对应像素点的匹配情况，共有三种状态：相互匹配记为 M、左可见右遮挡为 L、右可见左遮挡为 R，状态的选择满足无后效性。

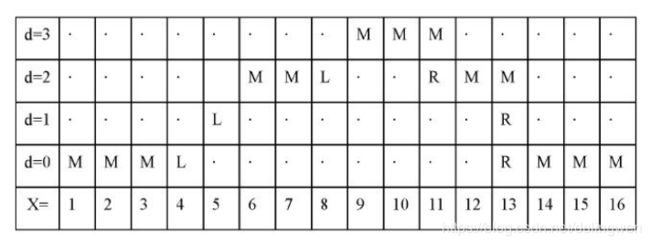
(3) 状态转移方程

  所谓状态转移方程就是根据前一阶段的状态确定当前阶段的状态，根据顺序性的约束，允许的状态转移的形式共有 7 种（用小写字母表示前一阶段的状态，写字母表示当前阶段的状态），如下图所示，其中 0 表示正确匹配，1、2 表示匹配产生左图像遮挡点，4、5 表示产生右图像遮挡点，3、6 表示图像由背景进入前景，视差跳变产生并不连续点。

(4) 求取最优解

  根据以上的理论分析，动态规划就是在校正图像上的每一行，寻找一条使得全局能量函数最小的最优匹配路径。能量函数一般定义如下：

其中 E(data)为图像数据项，用于判断匹配像素点之间的相似性， E(smooth)为像素点与邻域像素的平滑约束项, 用于保证视差的连续性。使用不同的能量函数优化得到的最终结果也会不同，因此构造能量函数也是十分重要的。在论文中，作者提出了一个具体的能量函数：

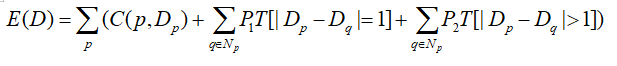
其中第一项为所有像素在视差图D下的匹配代价之和，第二项为当像素p和邻域像素q的视差差异为1时添加的常数惩罚值P1，第三项则添加了更大的惩罚值P2用于更大的视差差异。小的惩罚值能够适应倾斜表面和曲面，大的惩罚值能够适应深度不连续区域，由于深度不连续性一般出现在灰度发生跳变的地方，因此P2一般根据灰度梯度自适应的决定：

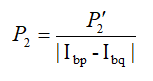
为了方便求解，不考虑顺序性约束和可见性约束，则求解过程如下：

按照上述过程，只要依次求解每个阶段的最优值$min{f}_k(d)$，该行像素的视差也就求出来了。从这个过程中可以发现，该计算流程实际上就是接下来所要讲解的SGM在水平方向上的代价聚合。

3.代价聚合

  全局立体匹配的过程可以认为是通过最小化全局能量函数来求得视差图，然而不幸的是，最小化这样一个2D全局能量函数是一个NP hard问题。在上一小节中介绍了在一维对极线上使用动态规划进行立体匹配的方法，该方法可以在多项式时间内完成能量最小化过程，然而算法最终得到的视差图中却会有明显的水平条纹，这是因为一维动态规划仅考虑了对极线上的约束，而对极线之间的约束却没有考虑。一些改进算法如行列双通道动态规划、基于垂直一致性加强约束的动态规划、基于树结构的动态规划可以有效改善这种问题，但这些算法都大大增加了运算复杂度。以上这些想法推动Hirschmuller提出了semi-global matching方法，如下图所示，其思想是通过在多个方向1维路径上平等地进行代价聚合，然后使用WTA求解视差，来作为一个近似求解2维能量最小化的过程。

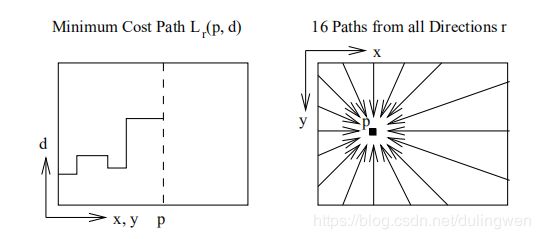
代价聚合按照如下公式递归计算：

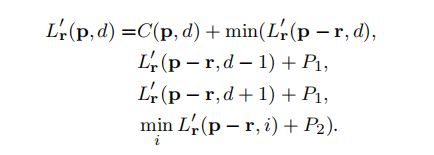
其中$r$代表一条路径，$p-r$代表沿着该路径上位于p前面的像素，代价$C(p,d)$可以为BT代价或者MI代价等。可以看出这种方法其实更加接近scanline optimization而非传统的动态规划。按照上述公式进行代价聚合，聚合值沿着路径会不断增加，最终将得到一个极大的数值，所以Hirschmuller建议采用如下改进的代价聚合公式：

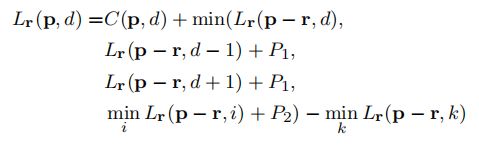
这个改进并不影响最后的计算结果，因为被减去的那项在像素p的不同视差下都对应一个常数，然而聚合代价的上限将会变为：$L<C_{max}+P_2$。代价聚合的路径可以为8或16个，这样可以全面覆盖整张图像，最终的聚合代价是所有路径上聚合代价的和：

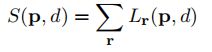
于是代价聚合的上限则变为：$L<16\ast (C_{max}+P_2)$，可以看到代价聚合的复杂度为$O(NWHD)$，其中N为代价聚合的路径数，W和H为图像的宽、高，D为视差搜索范围。由于代价聚合公式结构规整，操作简单，仅仅涉及了加减法和求最小，所以可以很容易的使用SIMD指令实现并行操作。

4.视差计算

经过代价聚合后，可以采用winner takes all方法来计算视差：

对于亚像素视差估计，可以通过抛物线拟合来求解。

5.多基线匹配

略，后续补充。

6.视差细化—后处理

初步计算出的视差不可避免地包含一些错误，因此需要采用一些方法去除或修正其中的错误视差。

6.1peak filter

  噪声、过饱和、大面积无纹理区域容易导致错误匹配，在生成的视差图中经常以块状聚集。对图像进行连通域分割，比如4连通或者8连通，然后通过一个预定义的尺寸阈值来判断这块连通域是否为噪声，若是则将其剔除。这种方法十分高效，可以在O(WH)步骤内完成。

6.2灰度一致性视差选择

略，后续补充

6.3无效视差值填充

  无效视差被分成两类：occlusions(遮挡)和mismatches(误匹配)，两种情形下的视差插值需要进行不同的处理，occlusions在邻域像素的视差中选择最小值，因为occlusions一般处于背景当中。mismatches一般取邻域像素的中值：

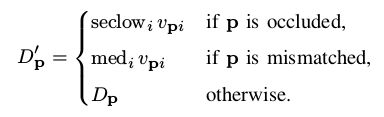
下面是Teddy图像的各个视差后处理的效果展示：

7.视差融合

略

三、OpenCV中的SGBM

​  在OpenCV中实现了SGM算法，叫做semi-global block matching，即SGBM，分为预处理、代价计算、代价聚合、后处理这四个步骤来实现。opencv在其中增加了一些独特的处理方法，下面分别说明一下各个步骤。
(1) 预处理
  SGBM 算法利用水平 Sobel 算子，对被测图片进行预处理，所用的到的算法公式如下式所示：

利用上面的函数公式会对水平 Sobel 算子对图片的所有的像素点进行处理过后，会变成一个崭新的图片(P的数值代表像素的像素值): $P_{NEW}$ 表示新图像上的像素值。映射函数公式如下式：

(2) 代价计算
  代价由两部分组成：一是对图像经过预处理后的梯度图计算BT代价，二是对没经过预处理的原图像计算BT代价，然后将两者简单相加，最后将得到的代价立方体在矩形窗口内进行求和：

(3) 代价聚合
即SGM中代价聚合的那一步。

(4) 后处理

A.唯一性检测
​  也就是常见的比率测试匹配筛选方法，即最低代价是次低代价的(1+ uniquenessRatio/100)倍的时候时，最低代价匹配的视差值才认为是正确视差值，否则这个像素点的视差值设定为负值。其中 uniquenessRatio 是一个常数参数，一般设置为0.8左右。

B.亚像素插值
插值公式如下：

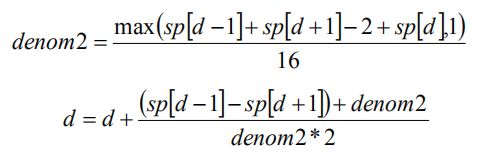
C.左右一致性检测
  设左图中像素$p$的视差为$d$，右图中对应像素的视差为$d^{\ast }$，那么一般认为$|d-d^{\ast }|<threshold$时，$d$才最有可能为正确的视差，否则将其置为一个无效值，即负值，threshold一般取为1或者2。

D.连通域噪声滤波

  连通域噪声滤波也就是作者在论文中所讲述的peak filter，这里就不重复叙述了。peak filter可以有效剔除噪声块，但是也很容易剔除正确的视差，使得整张视差图空洞比较多。

四、代码实现

这里采用opencv中已经封装好的SGBM算法，具体代码可以参考博客：双目测距理论及其python实现！

五、效果图

六、总结

1. SGM算法由于具有很高的匹配精度，并且可以从数据层面和多线程层面高度并行化处理，因此可以达到比较高的速度，使用GPU或FPGA甚至能够达到实时，因此SGM是至今最受欢迎的立体匹配算法，特别在商业应用中应该是使用最多的算法了。关于SGM算法的改进也非常多，除了opencv中的SGBM外，还有wSGM、rSGM、iSGM、MGM、tMGM-16、PMSGM、SGM-Forest、SGM-Net、GA-Net等等，有兴趣可以查阅相关论文阅读。
2. OpenCV在SGBM算法的后处理步骤中只有如何剔除错误视差的部分，而如何填补视差图上剔除后形成的空洞却没有相关的算法实现，而这一步对于后续的三维重建还是比较重要的。
3. SGBM算法的效果还是相当不错的，然而在实际应用当中，SGBM对于图像噪声、光照不均、大面积无纹理等各种情况依然不能很好的处理，真正的视差效果往往没有middleburry中的数据那样好，比如下图：
   
   还有的情况，SGBM算法几乎大面积失败了：
   
   如何处理实际场景中的图像特别是室外图像，需要有针对性的考虑，比如代价计算部分可以考虑对光照不均容忍性较强的census变换，或者考虑代价融合，其中比较有名的改进为ADCensus算法。