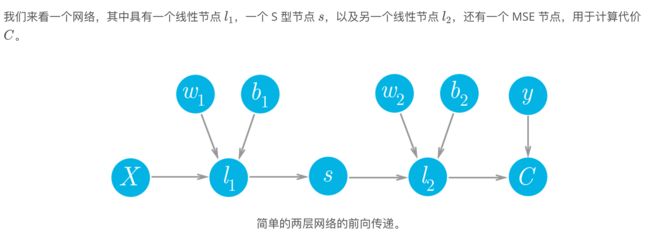
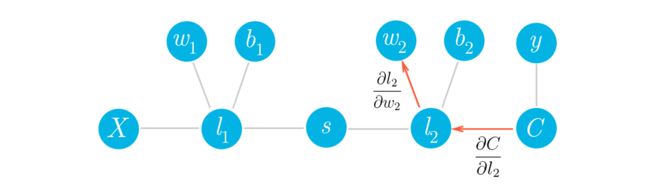
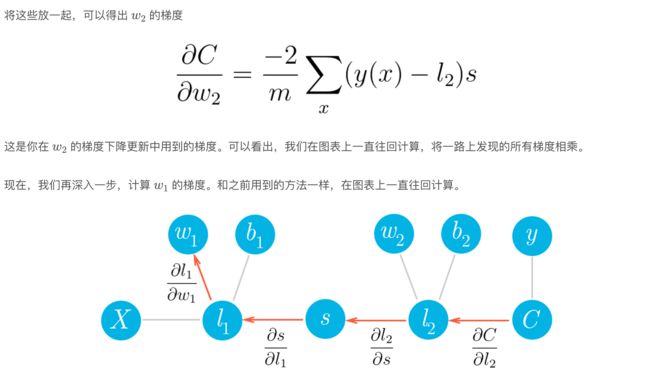
深度学习中的梯度和反向传播过程

类miniflow

"""
Implement the backward method of the Sigmoid node.
"""
import numpy as np


class Node(object):
    """
    Base class for nodes in the network.


    Arguments:


        `inbound_nodes`: A list of nodes with edges into this node.
    """
    def __init__(self, inbound_nodes=[]):
        """
        Node's constructor (runs when the object is instantiated). Sets
        properties that all nodes need.
        """
        # A list of nodes with edges into this node.
        self.inbound_nodes = inbound_nodes
        # The eventual value of this node. Set by running
        # the forward() method.
        self.value = None
        # A list of nodes that this node outputs to.
        self.outbound_nodes = []
        # New property! Keys are the inputs to this node and
        # their values are the partials of this node with
        # respect to that input.
        self.gradients = {}
        # Sets this node as an outbound node for all of
        # this node's inputs.
        for node in inbound_nodes:
            node.outbound_nodes.append(self)


    def forward(self):
        """
        Every node that uses this class as a base class will
        need to define its own `forward` method.
        """
        raise NotImplementedError


    def backward(self):
        """
        Every node that uses this class as a base class will
        need to define its own `backward` method.
        """
        raise NotImplementedError




class Input(Node):
    """
    A generic input into the network.
    """
    def __init__(self):
        # The base class constructor has to run to set all
        # the properties here.
        #
        # The most important property on an Input is value.
        # self.value is set during `topological_sort` later.
        Node.__init__(self)


    def forward(self):
        # Do nothing because nothing is calculated.
        pass


    def backward(self):
        # An Input node has no inputs so the gradient (derivative)
        # is zero.
        # The key, `self`, is reference to this object.
        self.gradients = {self: 0}
        # Weights and bias may be inputs, so you need to sum
        # the gradient from output gradients.
        for n in self.outbound_nodes:
            grad_cost = n.gradients[self]
            self.gradients[self] += grad_cost * 1




class Linear(Node):
    """
    Represents a node that performs a linear transform.
    """
    def __init__(self, X, W, b):
        # The base class (Node) constructor. Weights and bias
        # are treated like inbound nodes.
        Node.__init__(self, [X, W, b])


    def forward(self):
        """
        Performs the math behind a linear transform.
        """
        X = self.inbound_nodes[0].value
        W = self.inbound_nodes[1].value
        b = self.inbound_nodes[2].value
        self.value = np.dot(X, W) + b


    def backward(self):
        """
        Calculates the gradient based on the output values.
        """
        # Initialize a partial for each of the inbound_nodes.
        self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes}
        # Cycle through the outputs. The gradient will change depending
        # on each output, so the gradients are summed over all outputs.
        for n in self.outbound_nodes:
            # Get the partial of the cost with respect to this node.
            grad_cost = n.gradients[self]
            # Set the partial of the loss with respect to this node's inputs.
            self.gradients[self.inbound_nodes[0]] += np.dot(grad_cost, self.inbound_nodes[1].value.T)
            # Set the partial of the loss with respect to this node's weights.
            self.gradients[self.inbound_nodes[1]] += np.dot(self.inbound_nodes[0].value.T, grad_cost)
            # Set the partial of the loss with respect to this node's bias.
            self.gradients[self.inbound_nodes[2]] += np.sum(grad_cost, axis=0, keepdims=False)




class Sigmoid(Node):
    """
    Represents a node that performs the sigmoid activation function.
    """
    def __init__(self, node):
        # The base class constructor.
        Node.__init__(self, [node])


    def _sigmoid(self, x):
        """
        This method is separate from `forward` because it
        will be used with `backward` as well.


        `x`: A numpy array-like object.
        """
        return 1. / (1. + np.exp(-x))


    def forward(self):
        """
        Perform the sigmoid function and set the value.
        """
        input_value = self.inbound_nodes[0].value
        self.value = self._sigmoid(input_value)


    def backward(self):
        """
        Calculates the gradient using the derivative of
        the sigmoid function.
        """
        # Initialize the gradients to 0.
        self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes}


        # Cycle through the outputs. The gradient will change depending
        # on each output, so the gradients are summed over all outputs.
        for n in self.outbound_nodes:
            # Get the partial of the cost with respect to this node.
            grad_cost = n.gradients[self]
            """
            TODO: Your code goes here!


            Set the gradients property to the gradients with respect to each input.


            NOTE: See the Linear node and MSE node for examples.
            """
            self.gradients[self.inbound_nodes[0]]+=grad_cost*self._sigmoid(self.value))
        
            




class MSE(Node):
    def __init__(self, y, a):
        """
        The mean squared error cost function.
        Should be used as the last node for a network.
        """
        # Call the base class' constructor.
        Node.__init__(self, [y, a])


    def forward(self):
        """
        Calculates the mean squared error.
        """
        # NOTE: We reshape these to avoid possible matrix/vector broadcast
        # errors.
        #
        # For example, if we subtract an array of shape (3,) from an array of shape
        # (3,1) we get an array of shape(3,3) as the result when we want
        # an array of shape (3,1) instead.
        #
        # Making both arrays (3,1) insures the result is (3,1) and does
        # an elementwise subtraction as expected.
        y = self.inbound_nodes[0].value.reshape(-1, 1)
        a = self.inbound_nodes[1].value.reshape(-1, 1)


        self.m = self.inbound_nodes[0].value.shape[0]
        # Save the computed output for backward.
        self.diff = y - a
        self.value = np.mean(self.diff**2)


    def backward(self):
        """
        Calculates the gradient of the cost.


        This is the final node of the network so outbound nodes
        are not a concern.
        """
        self.gradients[self.inbound_nodes[0]] = (2 / self.m) * self.diff
        self.gradients[self.inbound_nodes[1]] = (-2 / self.m) * self.diff




def topological_sort(feed_dict):
    """
    Sort the nodes in topological order using Kahn's Algorithm.


    `feed_dict`: A dictionary where the key is a `Input` Node and the value is the respective value feed to that Node.


    Returns a list of sorted nodes.
    """


    input_nodes = [n for n in feed_dict.keys()]


    G = {}
    nodes = [n for n in input_nodes]
    while len(nodes) > 0:
        n = nodes.pop(0)
        if n not in G:
            G[n] = {'in': set(), 'out': set()}
        for m in n.outbound_nodes:
            if m not in G:
                G[m] = {'in': set(), 'out': set()}
            G[n]['out'].add(m)
            G[m]['in'].add(n)
            nodes.append(m)


    L = []
    S = set(input_nodes)
    while len(S) > 0:
        n = S.pop()


        if isinstance(n, Input):
            n.value = feed_dict[n]


        L.append(n)
        for m in n.outbound_nodes:
            G[n]['out'].remove(m)
            G[m]['in'].remove(n)
            # if no other incoming edges add to S
            if len(G[m]['in']) == 0:
                S.add(m)
    return L




def forward_and_backward(graph):
    """
    Performs a forward pass and a backward pass through a list of sorted Nodes.


    Arguments:


        `graph`: The result of calling `topological_sort`.
    """
    # Forward pass
    for n in graph:
        n.forward()


    # Backward pass
    # see: https://docs.python.org/2.3/whatsnew/section-slices.html
    for n in graph[::-1]:
        n.backward()

类nn.py

"""
Test your network here!


No need to change this code, but feel free to tweak it
to test your network!


Make your changes to backward method of the Sigmoid class in miniflow.py
"""


import numpy as np
from miniflow import *


X, W, b = Input(), Input(), Input()
y = Input()
f = Linear(X, W, b)
a = Sigmoid(f)
cost = MSE(y, a)


X_ = np.array([[-1., -2.], [-1, -2]])
W_ = np.array([[2.], [3.]])
b_ = np.array([-3.])
y_ = np.array([1, 2])


feed_dict = {
    X: X_,
    y: y_,
    W: W_,
    b: b_,
}


graph = topological_sort(feed_dict)
forward_and_backward(graph)
# return the gradients for each Input
gradients = [t.gradients[t] for t in [X, y, W, b]]


"""
Expected output


[array([[ -3.34017280e-05,  -5.01025919e-05],
       [ -6.68040138e-05,  -1.00206021e-04]]), array([[ 0.9999833],
       [ 1.9999833]]), array([[  5.01028709e-05],
       [  1.00205742e-04]]), array([ -5.01028709e-05])]
"""
print(gradients)