词的分布表示

词的表示

• One-hot Representation（独热表示）
  “苹果”表示为 [0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 …]
  优点：简介，缺点：词之间是孤立的，维数灾难。
• Distributed Representation（分布式表示）
  词向量或者词嵌入（word embedding）是用一个向量来表示一个词，一定程度上可以用来刻画词之间的语义距离。
  给出一个文档，用一个单词序列比如 “我喜欢苹果”，然后对文档中每个不同的单词都得到一个对应的低维向量表示，“苹果”表示为 [0.11, −0.77, −0.71, 0.10, −0.50, …]。
  优点：低维、相似词的词向量距离相近，缺点：计算复杂。

分布假说

上下文相似的词，其语义也相似。

语言模型

文本学习：词频、词的共现、词的搭配。
语言模型判定一句话是否为自然语言。机器翻译、拼写纠错、音字转换、问答系统、语音识别等应用在得到若干候选之后，然后利用语言模型挑一个尽量靠谱的结果。
n 元语言模型：对语料中一段长度为 n 的序列 wn−i+1,...,wi−1 ，即长度小于 n 的上文， n 元语言模型需要最大化如下似然：

P(wi|wn−i+1,...,wi−1)

wi 为语言模型要预测的 目标词，序列 wn−i+1,...,wi−1 为模型的输入，即上下文，输出则为目标词 wi 的分布。用频率估计估计 n 元条件概率：

P(wi|wn−i+1,...,wi−1)=count(wi|wn−i+1,...,wi−1,wi)count(wi|wn−i+1,...,wi−1)

通常， n 越大，越能保留词序信息，但是长序列出现的次数会非常少，导致数据稀疏的问题。一般三元模型较为常用。

基于矩阵的分布表示

基于矩阵的分布表示主要是构建“词-上下文”矩阵，通过某种技术从该矩阵中获取词的分布表示。矩阵的行表示词，列表示上下文，每个元素表示某个词和上下文共现的次数，这样矩阵的一行就描述了改词的上下文分布。常见的上下文有：（1）文档，即“词-文档”矩阵；（2）上下文的每个词，即“词-词”矩阵；（3）n-元词组，即“词-n-元组”矩阵。矩阵中的每个元素为词和上下文共现的次数，通常会利用TF-IDF、取对数等技巧进行加权和平滑。另外，矩阵的维度较高并且非常稀疏，可以通过SVD、NMF等手段进行分解降维，变为低维稠密矩阵。
经典模型代表：Global Vector模型（GloVe）。

GloVe模型（Global Vectors for Word Representation）

GloVe对“词-词”矩阵进行分解，只考虑矩阵非零的元素，同时采用了类似于推荐系统Latent Factor Model的方式进行矩阵分解。目标函数为：

J=∑xij≠0f(xij)(log(xij)−pTiqj+b(1)i+b(2)j)2

其中 b(1)i 和 b(2)j 为矩阵行和列的偏移项， f(xij) 是为了防止低频共现词的干扰对其进行衰减：

f(x)={(x/xmax)α,1,if x<xmaxotherwise

基于神经网络的分布表示

经典Bengio神经网络语言模型

Bengio 神经网络语言模型（Neural Network Language Model ，NNLM）是对 n 元语言模型进行建模，估算 P(wi|wn−i+1,...,wi−1) 的概率值。与n-gram等模型区别在于：NNLM不用记数的方法来估算 n 元条件概率，而是使用一个三层的神经网络模型（前馈神经网络），根据上下文的表示以及上下文与目标词之间的关系进行建模求解，如下图：

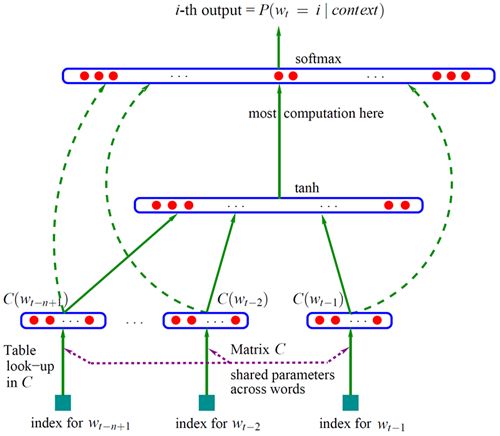
wt−1,...,wt−n+1 为 wt 之前的 n−1 个词，NNLM就是要根据这 n−1 个词预测下一个词 wt 。 C(w) 表示 w 对应的词向量，存储在矩阵 C 中， C(w) 为矩阵 C 中的一列，其中，矩阵 C 的大小为 m∗|V| ， |V| 为语料库中总词数， m 为词向量的长度。

• 输入层 x ：将 n−1 个词的对应的词向量 C(wt−n+1),...,C(wt−1) 顺序拼接组成长度为 (n−1)∗m 的列向量，用 x 表示，
  x=[C(wt−n+1),...,C(wt−1)]
• 隐含层 h ：使用 tanh 作为激励函数，输出
  tanh(d+Hx)
  ， Hh∗(n−1)m 为输入层到隐藏层的权重矩阵， d 为偏置项(biases)；
• 输出层 y ：一共有 |V| 个节点，分量 y(wt=i) 为上下文为 wt−n+1,...,wt−1 的条件下，下一个词为 wt 的可能性，即上下文序列和目标词之间的关系，而 yi 或者 y(wt) 是未归一化 log 概率(unnormalized log-probabilities)，其中， y 的计算为：
  y=b+Wx+Utanh(d+Hx)
  ， U|V|∗h 为隐藏层到输出层的权重矩阵， b 为偏置项， W|V|∗(n−1)m 为输入层到输出层直连边的权重矩阵，对输入层到输出层做一线性变换1。由于输出层的各个元素（ yi 或者 y(wt) ）之和不等于1，最后使用 softmax 激活函数将输出值 yi 进行归一化，将 y 转化为对应的概率值：
  
  P(wt|wt−n+1,...,wt−1)=eywt∑ieyvi

对于整个语料库，模型需要最大化：

∑wi−n+1:i∈VlogP(wi|wi−n+1,...,wi−1)

训练时使用梯度下降优化上述目标，每次训练从语料库中随机选取一段序列 wi−n+1,...,wi−1 作为输入，利用如下方式进行迭代：

θ⟵θ+α∂logP(wi|wi−n+1,...,wi−1)∂θ

其中， α 为学习速率， θ=(b,d,W,U,H,C) 。
相对于n-gram，NNLM的优势在于词语之|V|*h间的相似性可以通过词向量计算，比如：

• A cat is walking on the street * 10000
• A mouse is walking on the street * 1

上面例子中 cat 和 mouse 在NNLM中词向量相近，而在n-gram中cat的概率要大很多。

该结构的学习中，各层的规模：
输入层：n为上下文词数，一般不超过5，m为词向量维度，10~10^3；
隐含层：n_hidden，用户指定，一般为10^2量级；
输出层：词表大小V，10^4~10^5量级；
同时，也可以发现，该模型的计算主要集中在隐含层到输出层 tanh 的计算以及输出层 softmax 的计算。

word2vec

Bengio 等人的工作只考虑对语言模型的建模，词向量只是语言模型结束的副产品，因此他们并没有指出哪一套向量作为词向量效果更好。此外，在NNLM中词向量出现在两个地方，输入层各词的词向量是从矩阵 Cm∗|V| 中取出一列，隐含层到输出层的权重矩阵 U|V|∗h 中的向量是词向量的另一种表示 C′ ， C(w) 为词 w 作为上下文的表示， C′(w) 为词 w 作为目标词的表示。Mikolov 等人在NNLM等模型的基础之上，设计了CBOW（Continuous Bag-of-Words）和 Skip-gram 模型两个模型，高效地获取词向量。与NNLM不同的是，CBOW和Skip-gram中的目标词为词组的中间词，它的上下文共有 n−1 个词，前后各有 (n−1)/2 个词。

CBOW模型

CBOW模型对NNLM做了简化：
- 隐含层不再是上文各词词向量的拼接，而是使用上下文各词词向量的平均值，减少计算量；
- 去掉了tanh隐含层，提升模型训练速度；
CBOW模型包含3层，输入层、投影层和输出层：
- 输入层：共 n−1 个词的one-hot表示作为词向量，组成上下文的表示， C(wi−(n−1)/2),...C(wi−1),C(wi+1),...,C(wi−(n−1)/2)
- 投影层：将输入层的 n−1 个向量做均值计算， xi=1n−1∑i=(n−1/2)i=−(n−1)/2C(wi)
- 输出层：一共 |V| 个节点，第 i 个节点表示中心词是词 wi 的概率。CBOW 模型根据上下文的表示，直接对目标词进行预测：

P(wi|context(wi))=e(C′(wi)Tx)∑w′e(C′(w′i)Tx)

， w′i 为语料库中的某一各词。
对于整个语料库而言，CBOW的优化目标为最大化：

∑(w,context)logP(w|context(w))

Skip-gram模型

与 CBOW一样，Skip-gram模型中没有隐藏层，不同的是，Skip-gram模型每次从目标词 wi 的上下文context中选择一个词 wj ，将其词向量作为模型的输入 x ，作为上下文的表示，然后预测中心词。其中

P(wi|wj)=e(C′(wi)TC(wj))∑w′e(C′(w′i)TC(wj))

对于整个语料库而言，CBOW的优化目标为最大化：

∑w∑wj∈clogP(w|wj)

参考资料

[1] Yoshua Bengio, Rejean Ducharme, Pascal Vincent, and Christian Jauvin. A Neural Probabilistic Language Model. Journal of Machine Learning Research (JMLR), 3:1137–1155, 2003. [pdf]
[2] Tomas Mikolov et al. Efficient estimation of word representations in vector space. [pdf]
[2] 李泽魁。再探深度学习词向量表示(Advanced word vector representations)

---

1. Bengio 的论文中提到，如果使用该直连边，可以减少一半的迭代次数；但如果没有直连边，可以生成性能更好的语言模型。 ↩