梯度下降法的优化算法
如前文梯度下降法中所介绍的,梯度下降法存在如下问题导致其迭代的可行性和效率大打折扣:
(1)梯度不存在;
(2)非凸函数的鞍点和局部最优解;
(3)函数的信息利用率不高;
(4)学习率需预设且取值固定。
本文提到的梯度下降法的优化算法指:针对问题(2)、(3)和(4)提出的基于梯度下降法的Moment、AdaGrad和Adam等一系列算法。而这系列算法的核心改良思路包括两点:
(1)通过引入历史迭代点的信息,对当前点的梯度值进行修正。
(2)通过引入历史迭代点的信息,对当前点的学习率进行修正。
1. 常见的梯度下降法的优化算法
1.1. SGD+Momentum
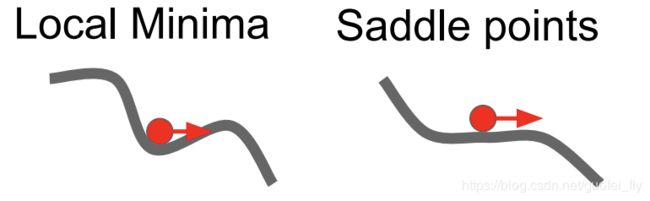
Momentum(动量)的灵感和效果非常类似于物理学里的动量项:如果迭代点在梯度为0处保持一定的速度(动量),则很有可能会冲破局部最优点或鞍点的束缚进行继续的搜索,从而发现更优的取值。
那么如何设置动量项呢?通过过往迭代点的历史梯度信息值进行构造! 从数学公式上看,其迭代过程为: v 0 = 0 v t = ρ v t − 1 − α g t − 1 x t = x t − 1 + v t \begin{aligned}&v_0=0\\&v_t=\rho v_{t-1}-\alpha g_{t-1}\\&x_t=x_{t-1}+v_t\end{aligned} v0=0vt=ρvt−1−αgt−1xt=xt−1+vt式中, v t v_t vt为第 t t t步迭代时的动量项,其初始指 v 0 v_0 v0为0, g t − 1 g_{t-1} gt−1为第 t t t步迭代时在当前点处的梯度值, α \alpha α为学习率, ρ \rho ρ的作用类似于摩擦系数,对过往的梯度和起到衰减的作用,其常取用指为0.9、0.99。
可见,SGD+Momentum就是将原始梯度下降法中的每轮迭代处梯度指改为历史梯度指的加权和。从而使得在鞍点或局部最优点,仍能有一定的速度继续迭代。

此外,SGD+Momentum还有其它多种写法,但其本质都是一样的。如: v 0 = 0 v t = ρ v t − 1 + g t − 1 x t = x t − 1 − α v t \begin{aligned}&v_0=0\\&v_t=\rho v_{t-1}+g_{t-1}\\&x_t=x_{t-1}-\alpha v_t\end{aligned} v0=0vt=ρvt−1+gt−1xt=xt−1−αvt
1.2. Nesterov Momentum
Nesterov Momentum和SGD+Momentum的做法非常类似,只是将其中的梯度项 g t g_t gt略作修改,将当前迭代点 x t x_t xt改为 x t + ρ v t x_t+\rho v_t xt+ρvt。其迭代公式为: v 0 = 0 v t = ρ v t − 1 − α ∇ f ( x t − 1 + ρ v t − 1 ) x t = x t − 1 + v t \begin{aligned}&v_0=0\\&v_t=\rho v_{t-1}-\alpha \nabla f(x_{t-1}+\rho v_{t-1})\\&x_t=x_{t-1}+v_t\end{aligned} v0=0vt=ρvt−1−α∇f(xt−1+ρvt−1)xt=xt−1+vt若令 x ~ t − 1 = x t − 1 + ρ v t − 1 \tilde x_{t-1}=x_{t-1}+\rho v_{t-1} x~t−1=xt−1+ρvt−1,则 x ~ t = x t + ρ v t = x ~ t − 1 + v t + ρ ( v t − v t − 1 ) \tilde x_{t}=x_t+\rho v_t=\tilde x_{t-1}+v_t+\rho(v_t-v_{t-1}) x~t=xt+ρvt=x~t−1+vt+ρ(vt−vt−1),可将迭代公式进一步写为: v 0 = 0 v t = ρ v t − 1 − α ∇ f ( x ~ t − 1 ) x ~ t = x ~ t − 1 + v t + ρ ( v t − v t − 1 ) \begin{aligned}&v_{0}=0\\&v_t=\rho v_{t-1}-\alpha \nabla f(\tilde x_{t-1})\\&\tilde x_{t}=\tilde x_{t-1}+v_t+\rho(v_t-v_{t-1})\end{aligned} v0=0vt=ρvt−1−α∇f(x~t−1)x~t=x~t−1+vt+ρ(vt−vt−1)

1.3. AdaGrad
AdaGrad是一种对梯度下降法中学习率的自适应策略,其通过构造历史迭代点梯度值平方和来实现学习率的自适应变化,其迭代方法为: s 0 = 0 s t = s t − 1 + g t − 1 ⊙ g t − 1 x t = x t − 1 − α s t + ϵ ⊙ g t − 1 \begin{aligned}&s_0=0\\&s_t=s_{t-1}+g_{t-1}\odot g_{t-1}\\&x_t=x_{t-1}-\frac{\alpha}{\sqrt{s_t+\epsilon}}\odot g_{t-1}\end{aligned} s0=0st=st−1+gt−1⊙gt−1xt=xt−1−st+ϵα⊙gt−1式中, ⊙ \odot ⊙表示逐元素内积; s t s_t st为第 t t t迭代时历史梯度平方值的和,其初始值为0; g t − 1 g_{t-1} gt−1为第 t t t迭代时在当前点处的梯度值; α \alpha α为约束学习率; ϵ \epsilon ϵ为平滑算子,用于避免分母为0的问题,其常用取值为 1 ∗ 1 0 − 7 1*10^{-7} 1∗10−7。
AdaGrad的方法有两个显而易见的好处:
(1)各个变量方向的学习率是不一样的,梯度值大(函数曲面陡)的方向学习率小,而梯度下(函数曲面平坦)的方向学习率大。从而有效回避了传统梯度下降法中由于固定学习率,在高条件数下的迭代震荡问题(见下图)。

(2)学习率随着迭代步数的增加而逐渐减小,从而达到了以先加速学习,再稳步学习的目的。
但随着AdaGrad的迭代步数增加,学习率会逐渐趋向于0,可能导致后期迭代不动的问题。针对该问题,学者们又提出了RMSProp方法。
1.4. RMSProp
RMSProp沿用了AdaGrad的核心思想,知识将历史迭代点梯度值平方和变为历史迭代点梯度值平方的指数加权移动平均数,从而防止了学习率会逐渐趋向于0,其迭代方法为: s 0 = 0 s t = ρ s t − 1 + ( 1 − ρ ) g t − 1 ⊙ g t − 1 x t = x t − 1 − α s t + ϵ ⊙ g t − 1 \begin{aligned}&s_0=0\\&s_t=\rho s_{t-1}+(1-\rho)g_{t-1}\odot g_{t-1}\\&x_t=x_{t-1}-\frac{\alpha}{\sqrt{s_t+\epsilon}}\odot g_{t-1}\end{aligned} s0=0st=ρst−1+(1−ρ)gt−1⊙gt−1xt=xt−1−st+ϵα⊙gt−1
1.5. AdaDelta
AdaDelta和RMSProp非常类似,只是多引入了一个用于记录历史迭代点梯度值的指数加权移动平均数的变量 Δ x \Delta x Δx,其迭代公式为: s 0 = 0 , Δ x 0 = 0 s t = ρ s t − 1 + ( 1 − ρ ) g t − 1 ⊙ g t − 1 g ~ t = Δ x t − 1 + ϵ s t + ϵ ⊙ g t − 1 x t = x t − 1 − g ~ t Δ x t = ρ Δ x t − 1 + ( 1 − ρ ) g ~ t ⊙ g ~ t \begin{aligned}&s_0=0,\Delta x_0=0\\&s_t=\rho s_{t-1}+(1-\rho)g_{t-1}\odot g_{t-1}\\&\tilde g_{t}=\sqrt\frac{\Delta x_{t-1}+\epsilon}{s_t+\epsilon}\odot g_{t-1}\\&x_t=x_{t-1}-\tilde g_t\\&\Delta x_t =\rho\Delta x_{t-1}+(1-\rho) \tilde g_t\odot \tilde g_t\end{aligned} s0=0,Δx0=0st=ρst−1+(1−ρ)gt−1⊙gt−1g~t=st+ϵΔxt−1+ϵ⊙gt−1xt=xt−1−g~tΔxt=ρΔxt−1+(1−ρ)g~t⊙g~t如果不考虑 ϵ \epsilon ϵ的影响,AdaDelta与RMSProp的区别仅在于使用 Δ x t − 1 \sqrt{\Delta x_{t-1}} Δxt−1替代预设的学习率 α \alpha α,从而减少了一个参数。
1.6. Adam
Adam同时采用了动量项和自适应学习率的策略,其分别计算梯度值和梯度值平方的指数加权移动平均数进行迭代: m 0 = 0 , v 0 = 0 m t = β 1 m t − 1 + ( 1 − β 1 ) g t − 1 v t = β 2 v t − 1 + ( 1 − β 2 ) g t − 1 ⊙ g t − 1 x t = x t − 1 − α v t + ϵ m t \begin{aligned}&m_0=0,v_0=0\\&m_t=\beta_1 m_{t-1}+(1-\beta_1)g_{t-1}\\&v_t=\beta_2 v_{t-1}+(1-\beta_2)g_{t-1}\odot g_{t-1}\\&x_t=x_{t-1}-\frac{\alpha}{\sqrt{v_t}+\epsilon}m_t\end{aligned} m0=0,v0=0mt=β1mt−1+(1−β1)gt−1vt=β2vt−1+(1−β2)gt−1⊙gt−1xt=xt−1−vt+ϵαmt式中, β 1 \beta_1 β1和 β 2 \beta_2 β2均为指数加权移动平均数的参数,而 α \alpha α为学习率。
考虑到若初始化条件为0,则结果会发生偏置,因此进行了如下校正: m 0 = 0 , v 0 = 0 m t = β 1 m t − 1 + ( 1 − β 1 ) g t − 1 v t = β 2 v t − 1 + ( 1 − β 2 ) g t − 1 ⊙ g t − 1 m ^ t = m t 1 − β 1 t v ^ t = v t 1 − β 2 t x t = x t − 1 − α v ^ t + ϵ m ^ t \begin{aligned}&m_0=0,v_0=0\\&m_t=\beta_1 m_{t-1}+(1-\beta_1)g_{t-1}\\&v_t=\beta_2 v_{t-1}+(1-\beta_2)g_{t-1}\odot g_{t-1}\\&\hat m_t=\frac{m_t}{1-\beta_1^t}\\&\hat v_t=\frac{v_t}{1-\beta_2^t}\\&x_t=x_{t-1}-\frac{\alpha}{\sqrt{\hat v_t}+\epsilon}\hat m_t\end{aligned} m0=0,v0=0mt=β1mt−1+(1−β1)gt−1vt=β2vt−1+(1−β2)gt−1⊙gt−1m^t=1−β1tmtv^t=1−β2tvtxt=xt−1−v^t+ϵαm^t其中超参数的建议预设值为: β 1 = 0.9 , β 2 = 0.999 , ϵ = 1 ∗ 1 0 − 8 \beta_1=0.9,\beta_2=0.999,\epsilon=1*10^{-8} β1=0.9,β2=0.999,ϵ=1∗10−8
对比 RMSprop 算法,Adam可理解成在RMSprop基础上加了 bias-correction 和 momentum。
2. 优化算法对比
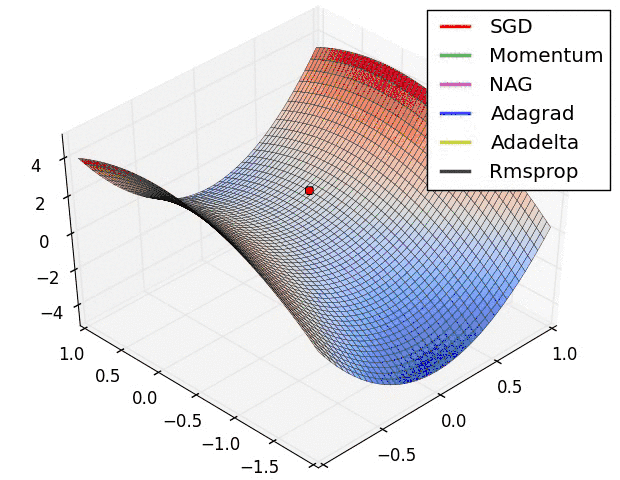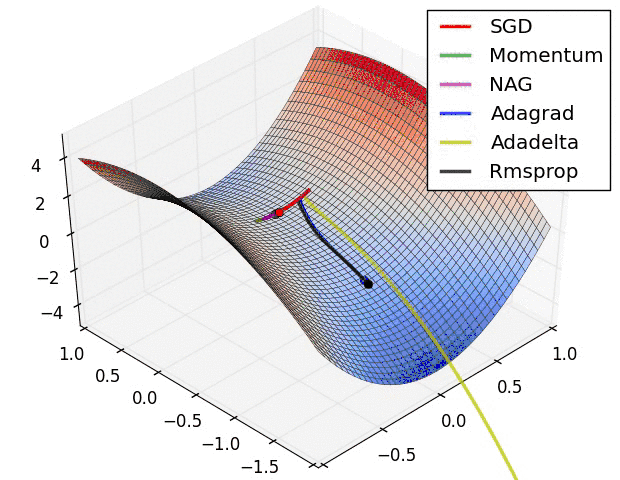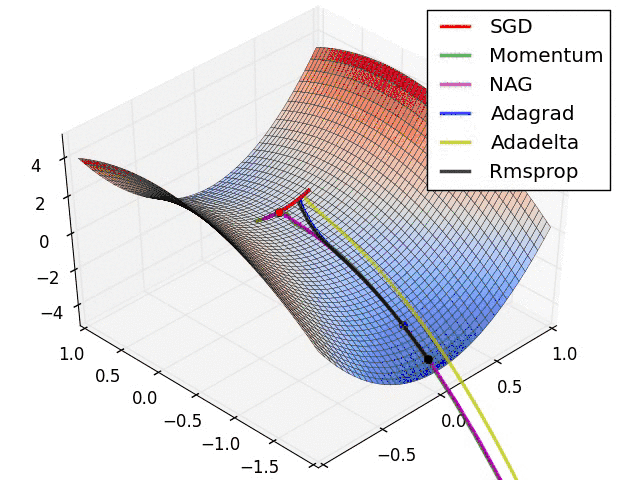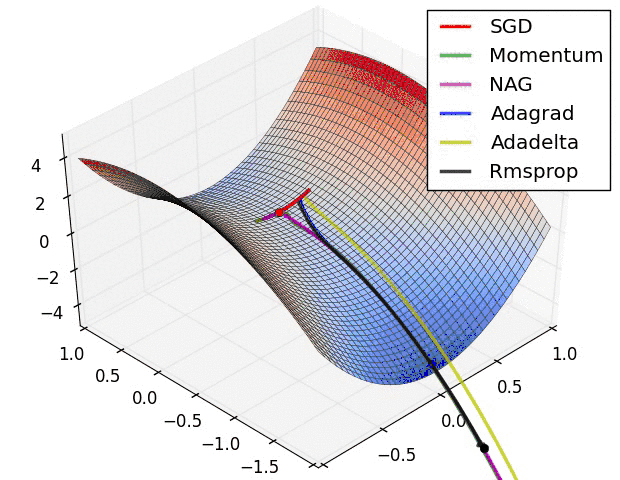
下图为上述各种算法在等高线上的表现:

由此可见,在这种情况下,Adagrad, Adadelta, RMSprop 几乎很快就找到了正确的方向并前进,收敛速度也相当快,而其它方法要么很慢,要么走了很多弯路才找到。
3. 优化算法的选用策略
(1)整体而言,Adam 是最好的选择。所以常用做默认的优化算法;
(2)面对稀疏数据,需选择自适用方法,即 Adagrad, Adadelta, RMSprop, Adam;
(3)随着梯度变的稀疏,Adam 比 RMSprop 效果会好;
(4)若自适应的算法不佳,仍可考虑采用传统的SGD算法。