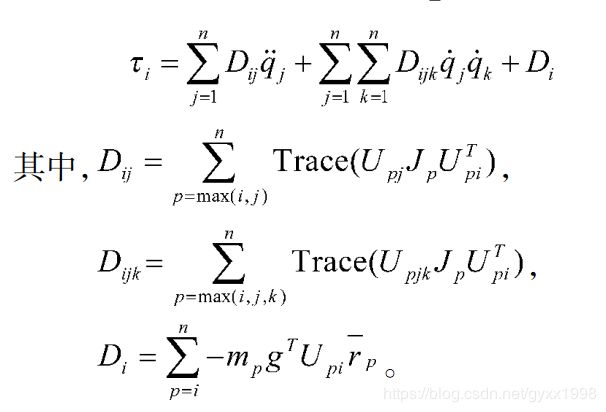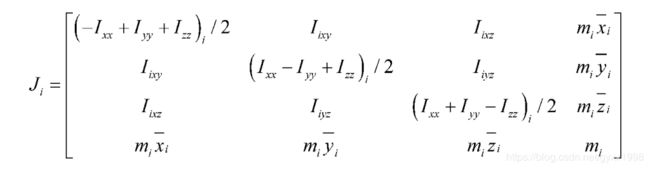Matlab机器人工具箱（3-3）：五自由度机械臂（动力学）

动力学主要分为牛顿-欧拉法和拉格朗日法

• 牛顿-欧拉法：
  向外递推速度与角速度，向内迭代计算力与力矩

• 拉格朗日方程：
  根据能量思想，从标量（拉格朗日方程）得到动力学方程
  先计算动能与势能，再构造拉格朗日方程，最后对广义变量（关节角度）求导，得到力矩

单位的说明：

• sw得到的
  惯性张量单位是 千克·平方毫米
  位置是 毫米
  质量是 kg
• 如果加速度单位为 m·s-2，即 N/kg
• 那么最后计算出的力矩的单位是 N·mm

参考：

• 动力学方法讲解
• 百度文库：11.5操作臂动力学

01 准备工作：为机械臂模型中加入动力学参数

• 需要得到每个关节的 质量，质心位置，惯性张量
• 以上数据通常在SolidWorks中获得（指定材质→测量-质量属性）
  （可以先在关节角处创建一个坐标系，在质量属性的测量中指定输出坐标系）
  参考：https://blog.csdn.net/weixin_43455581/article/details/103579030
• 加入动力学参数后的机械臂模型，并保存为 mdl_Dyn_5dof.m

% mdl_Dyn_5dof.m
% 单臂动力学结构参数
d=[        0,     0,        0,        0,       0];
a=[        0,    13,   233.24,   175.64,       0];%/1000
alpha=[    0,  pi/2,        0,        0,    pi/2];

%使用offset
L(1)=Link('d',d(1),'a',a(1),'alpha',alpha(1),'modified'); 
L(2)=Link('d',d(2),'a',a(2),'alpha',alpha(2),'offset',pi/2,'modified');
L(3)=Link('d',d(3),'a',a(3),'alpha',alpha(3),'modified');
L(4)=Link('d',d(4),'a',a(4),'alpha',alpha(4),'offset',pi/2,'modified');
L(5)=Link('d',d(5),'a',a(5),'alpha',alpha(5),'modified');

du=pi/180;
ra=180/pi;
%定义关节范围
L(1).qlim =[-170, 170]*du;
L(2).qlim =[60-70, 60+70]*du;%-10,130
L(3).qlim =[-70-70,-70+70]*du;%-140,0
L(4).qlim =[-70,70]*du;
L(5).qlim =[-170, 170]*du;
bot=SerialLink(L,'name','五自由度机械臂');
%bot.tool= transl(0, 0, tool)

% 动力学参数
data=[
    %     Ixx，    Iyy,      Izz,        Ixy,        Ixz,        Iyz,         xc,         yc,        zc,       m
       47.316,  51.601,   77.113,     -0.003,     -2.549,     -0.016,     -0.598,      0.016,   -23.413,   0.076;
       62.746, 651.130,  704.486,     29.632,     -0.001,     -0.003,    104.910,    -31.512,     0.001,   0.151;
        6.264, 224.674,  228.590,    -14.345,     -0.006,          0,     69.863,      8.061,     0.015,   0.065;
        1.502,   1.800,    2.241,      0.455,          0,          0,      4.498,    -12.503,         0,   0.008;
       13.735,  14.594,   15.321,          0,      0.004,          0,      0.046,          0,    43.571,   0.036
    ];

% data(:,1:6)=data(:,1:6)./1000000;
% data(:,7:9)=data(:,7:9)./1000;

% 惯性张量
data(:,[5 6])=data(:,[6 5]);%交换Ixz和Iyz
for i=1:5
   %I = [L_xx, L_yy, L_zz, L_xy, L_yz, L_xz]
   %放入是6个数字，但存储是矩阵形式的9个数字
   bot.links(i).I=data(i,1:6); 
end

%质心
for i=1:5
   bot.links(i).r=data(i,7:9); 
end

% 质量
for i=1:5
   bot.links(i).m=data(i,10); 
end

% 对于空中机械臂，重力与坐标系方向一致，所以为正
% 这与matlab自带的重力系统相反，所以matlab自带函数为负
% 重力单位是m·s-2，也是N/kg,考虑到第二种意义，这里不改变数量值
bot.gravity=[0;0;-9.81];

02 机器人工具箱函数

2.1 正动力学

• fdyn()
• accel()
  
  

% torqfun = [0,30,6,0,0,0];%设定一组关节力
bot_nf=bot.nofriction();
[T,q,qd] = bot_nf.fdyn(1, torqfun)
for i=1:65,
	qdd = bot_nf.accel(q(i,:),qd(i,:),torqfun)
end

2.2 逆动力学

• tau = R.rne(q, qd, qdd, grav, fext)

2.3 重力载荷

• bot.gravload(q)
  
  

% RoboticToolbox v10
% 动力学：使用原有工具箱函数
% 绘制静止状态关节2/3的重力载荷图
mdl_Dyn_5dof
du=pi/180;
ra=180/pi;
%% test:比较重力正负的影响
bot.gravity=[0;0;9.81];
tau1=bot.gravload([30,30,-30,30,30]*du);
% 上述两句等价于
% tau3=bot.rne([30,30,-30,30,30]*du,[0 0 0 0 0],[0 0 0 0 0],[0 0 9.8])
bot.gravity=[0;0;-9.81];
tau2=bot.gravload([30,30,-30,30,30]*du);


%% 数据
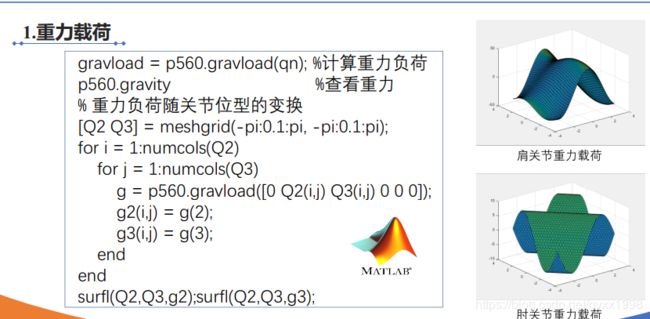
% gravload = p560.gravload(qn); %计算重力负荷
bot.gravity %查看重力
% 重力负荷随关节位型的变换
[q2_st,q2_end]=deal(bot.links(2).qlim(1),bot.links(2).qlim(2));%关节2坐标范围
[q3_st,q3_end]=deal(bot.links(3).qlim(1),bot.links(3).qlim(2));%关节3坐标范围
[Q2 Q3] = meshgrid(q2_st:0.1:q2_end, q3_st:0.1:q3_end);
% [Q2 Q3] = meshgrid(-pi:0.1:pi, -pi:0.1:pi);
for i = 1:numcols(Q2)
    for j = 1:numcols(Q3)
        g = bot.gravload([0 Q2(i,j) Q3(i,j) 0 0]);%关节2/3设置角度，其余设置为0
        g2(i,j) = g(2);
        g3(i,j) = g(3);
    end
end

%% 绘图
figure('name','肩关节重力载荷')
% 单位deg
Q2du=Q2*ra;Q3du=Q3*ra;
surfl(Q2du,Q3du,g2);
xlabel('\theta_2(deg)');ylabel('\theta_3(deg)');zlabel('关节2重力载荷');
% 单位rad
% surfl(Q2,Q3,g2);
% xlabel('\theta_2(rad)');ylabel('\theta_3(rad)');zlabel('关节2重力载荷');

figure('name','肘关节重力载荷')
surfl(Q2du,Q3du,g3)
xlabel('\theta_2(deg)');ylabel('\theta_3(deg)');zlabel('关节3重力载荷');
% surfl(Q2,Q3,g3)
% xlabel('\theta_2(rad)');ylabel('\theta_3(rad)');zlabel('关节3重力载荷');

2.4 惯性矩阵&科氏矩阵

03 自己写的 拉格朗日方程 的函数

可参考论文

• 《仿生四足-轮复合移动机构设计与多运动模式步态规划研究》
• 《六自由度工业机械臂动力学模型简化分析》

其中

• 拉格朗日方程求解力矩的函数为：

% 逆动力学求解函数
% 输入 机械臂名称，位置、速度、加速度矩阵
% 输出关节扭矩
% 是MDH_Dy.m的改进版，使用offset
% 改进体现在直接使用机器人的某些参数
function [ t ] = MDH_Dyn( robot,Q,DQ,DDQ )
    global T_cell;
    %% 关节角度
%     syms q1 q2 q3 q4 q5;
%     syms dq1 dq2 dq3 dq4 dq5;
%     syms ddq1 ddq2 ddq3 ddq4 ddq5;
    [q1,q2,q3,q4,q5]=deal(Q(1),Q(2),Q(3),Q(4),Q(5));
    [dq1,dq2,dq3,dq4,dq5]=deal(DQ(1),DQ(2),DQ(3),DQ(4),DQ(5));
    [ddq1,ddq2,ddq3,ddq4,ddq5]=deal(DDQ(1),DDQ(2),DDQ(3),DDQ(4),DDQ(5));
    %% 计算伪惯量矩阵
    J_cell=cell(5,1);
    %Ixx，Iyy,Izz,  Ixy,Ixz,Iyz,  xc,yc,zc,m
    %长度单位mm，惯性张量kg*mm，
    data=[
    %     Ixx，    Iyy,      Izz,        Ixy,        Ixz,        Iyz,         xc,         yc,        zc,       m
       47.316,  51.601,   77.113,     -0.003,     -2.549,     -0.016,     -0.598,      0.016,   -23.413,   0.076;
       62.746, 651.130,  704.486,     29.632,     -0.001,     -0.003,    104.910,    -31.512,     0.001,   0.151;
        6.264, 224.674,  228.590,    -14.345,     -0.006,          0,     69.863,      8.061,     0.015,   0.065;
        1.502,   1.800,    2.241,      0.455,          0,          0,      4.498,    -12.503,         0,   0.008;
       13.735,  14.594,   15.321,          0,      0.004,          0,      0.046,          0,    43.571,   0.036
    ];

%     data=[
%         22.134, 30.762, 24.755, -2.241, -0.00, 0, -2.546, -21.352, 0.302, -2.948;
%         85.387, 822.001, 893.708, 48.758, 0, 0, 102.348, -34.530, 0, 0.223;
%         5.440, 281.010, 283.608,  -17.983, 0, 0, 68.088, 7.699, 0, 0.084;
%         1.541, 1.748, 2.151, 0.404, 0, 0, 3.601, -12.855, 0, 0.009;
%         8.962, 9.856, 8.307, 0, 0, 0, 0, 0, -2.222, 0.025
%         ];
    for i=1:5
        Ixx=data(i,1);Iyy=data(i,2);Izz=data(i,3);
        Ixy=data(i,4);Ixz=data(i,5);Iyz=data(i,6);
        xc=data(i,7);yc=data(i,8);zc=data(i,9);
        m=data(i,10);

        J=[(-Ixx+Iyy+Izz)/2,Ixy,Ixz,m*xc;
            Ixy,(Ixx-Iyy+Izz)/2,Iyz,m*yc;
            Ixz,Iyz,(Ixx+Iyy-Izz)/2,m*zc;
            m*xc,m*yc,m*zc,m];

        J_cell{i}=J;   
    end
    %%
    T_cell=cell(5,1);
    q=[q1,q2,q3,q4,q5];
    for i=1:5
        T_cell{i}=robot.links(i).A(q(i)).T;
    end
    %%
    % t=zeros(5,1);
    % Dij=zeros(5,5);
    % Dijj=zeros(5,5);
    % Dijk=zeros(5,10);
    % Di=zeros(5,1);
    q=[q1;q2;q3;q4;q5];
    dq=[dq1;dq2;dq3;dq4;dq5];
    ddq=[ddq1;ddq2;ddq3;ddq4;ddq5];
    dqdq=[dq1*dq2;dq1*dq3;dq1*dq4;dq1*dq5;
        dq2*dq3;dq2*dq4;dq2*dq5;
        dq3*dq4;dq3*dq5;
        dq4*dq5];
    %% Dij
    %行
    for i=1:5
        %列
        for j=1:5
            p=max(i,j);
            %累加
            D=0;
            for pp=p:5          
                Upj=Uij(pp,j);
                Upi=Uij(pp,i);
                D=D+trace(Upj*J_cell{pp}*Upi.');           
            end
            Dij(i,j)=D;
        end
    end
    %% Dijj
    for i=1:5
        for j=1:5
            p=max(i,j);
            %累加
            D=0;
            for pp=p:5          
                Upjj=Uijk(pp,j,j);
                Upi=Uij(pp,i);
                D=D+trace(Upjj*J_cell{pp}*Upi.');           
            end
            Dijj(i,j)=D;
        end
    end
    %% Dijk
    %标记标号j和k，for循环记录不太方便，所以直接写下来
    dijk_j=[1,1,1,1,2,2,2,3,3,4];
    dijk_k=[2,3,4,5,3,4,5,4,5,5];
    %行
    for i=1:5
        %列循环
        for s=1:10
            %列内标号循坏
            j=dijk_j(1,s);
            k=dijk_k(1,s);
            %p=max(i,j,k)
            p=max(i,j);
            p=max(p,k);
            %累加
            D=0;
            for pp=p:5
              Upjk=Uijk(pp,j,k);
              Upi=Uij(pp,i);
              D=D+trace(Upjk*J_cell{pp}*Upi.');  
            end
            Dijk(i,s)=D;
        end
    end
    %% Di
    for i=1:5
        D=0;
        %累加
        for p=i:5
           m_p=data(p,10);
           %位置和加速度都是齐次
           gT=[0,0,9.81,0];%空中机械臂重力与坐标系方向一致，所以为正
           Upi=Uij(p,i);
           %位置是在p坐标系下 r是1×4的列矩阵
           r_cp=[data(p,7);data(p,8);data(p,9);1];
           D=D+m_p*gT*Upi*r_cp;%前两个关节力矩都为0，Up2只在后两行为0，g只在第三行不为0
        end
        Di(i,1)=-D;
    end
    %% 计算
    t= Dij*ddq + Dijj*(dq.^2) + 2*Dijk*dqdq +Di; 
    %%
    t=t';
end

• 其中Uij为

% 计算拉格朗日动力学参数Uij
% 在MDH_Dy中使用
function [ U ] = Uij( i,j )
    global T_cell;
%旋转矩阵对角度求导
   Q=[0, -1, 0, 0;
      1,  0, 0, 0;
      0,  0, 0, 0;
      0,  0, 0, 0];
   U=1;
   for kk=1:j
        U=U*T_cell{kk};
    end
    
    U=U*Q;
    
    for kk=j+1:i
        U=U*T_cell{kk};
    end

end

• 其中Uijk为

% 计算拉格朗日动力学参数Uij
% 在MDH_Dy中使用
function [ U ] = Uijk(  i,j,k )
   global T_cell;
   Q=[0, -1, 0, 0;
       1,  0, 0, 0;
       0,  0, 0, 0;
       0,  0, 0, 0];
   U=1;
   for p=1:j-1
        U=U*T_cell{p};
   end
    
   U=U*Q;
   %for先判断再循坏 
   for p=j:k-1
        U=U*T_cell{p};
   end
    
   U=U*Q;
    
   for p=k:i
        U=U*T_cell{p};
   end

end