LeetCode刷题Easy篇寻找最大和的连续子数组（kadane算法和动态规划）

 

题目

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Follow up:

If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

 

我的尝试

寻找一个连续的子数组，和为最大，并且时间复杂度为O（n）

这是一个动态规划问题，尝试用以前的滑动窗口思路，没解决，看了一下资料，采用kadane算法可以解决。link如下：

https://www.geeksforgeeks.org/largest-sum-contiguous-subarray/

我尝试写出来自己的代码：

package com.puhui.goosecard.manage;
 
/**
 * 2 * @Author: kerry
 * 3 * @Date: 2018/12/7 10:18
 * 4
 */
public class Test {
 
 
    public static int kandane(int[] nums) {
        int currMax = nums[0];
        int maxSoFar = nums[0];
        //注意从1开始
        for (int i = 1; i < nums.length; i++) {
            currMax = Math.max(nums[i], currMax + nums[i]);
            maxSoFar = Math.max(currMax, maxSoFar);
        }
        return maxSoFar;
 
    }
 
 
    public static void main(String[] args) {
        int[] nums = {2, 4, 0, -4, 6, -8, 1};
        System.out.println(kandane(nums));
 
    }
}

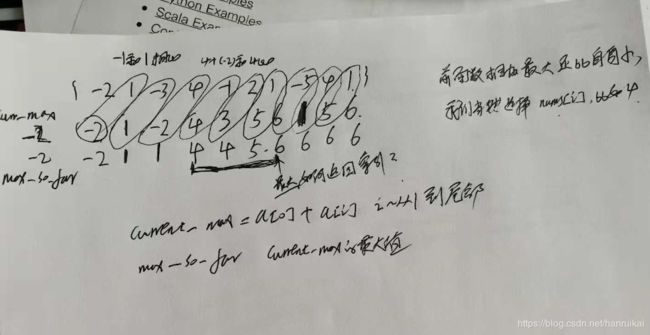
看似很简单 代码，其实不是很容易理解，这个算法的过程网上有一大堆，但是你不是很能明白，建议自己推导理解一下，下面是我的手写过程。

其实认真理解一下，current_max就是截止到当前元素的最大和，一种是元素自己本身，因为前面的和小于0，或者是前面全部累加或者部分累加的和。总而言之，current_max就是某个元素为止的最大和。另外一个so far用来比较这些和，找出最大的就是我们所求的。

优化解法

上面的算法比较晦涩，虽然看似简单，而且不具有通用性，发现有网友利用dp解决了这个问题。我对dp对理解不够，重新复习一下dp的解题思路：

实际应用中能够按下面几个简化的步骤进行设计：

（1）分析最优解的性质。并刻画其结构特征。

（2）递归的定义最优解。

（3）以自底向上或自顶向下的记忆化方式（备忘录法）计算出最优值。

（4）依据计算最优值时得到的信息，构造问题的最优解。

虽然现在不能运用自如，但是假以时日，肯定可以灵活掌握动态规划，以本题目为例应用动态规划：

第一步：分析

分析最优解性质和特征：连续子数组，和最大

第二步：递归定义最优解

递归定义最优解 ，这个步骤非常重要，对于一个数组A，截止到元素i的子数组中最大和可以定义为

maxSubArray(A, i) = maxSubArray(A, i - 1) > 0 ? maxSubArray(A, i - 1) : 0 + A[i]; 

解释一下，前i个元素，如果和最大，那么前i-1个元素如果大于0，直接相加就可以，反之如果前i-1个元素和小于0，则直接取0即可。

第三步 ：备忘录记录

定义一个数组dp，存储截止到元素i的最大和值。

dp[0]=A[0];

public int maxSubArray(int[] A) {
        int n = A.length;
        int[] dp = new int[n];//dp[i] means the maximum subarray ending with A[i];
        dp[0] = A[0];
        int max = dp[0];
        
        for(int i = 1; i < n; i++){
            dp[i] = A[i] + (dp[i - 1] > 0 ? dp[i - 1] : 0);
            max = Math.max(max, dp[i]);
        }
        
        return max;
}

整理思路

在上面的dp思路，有人指出不需要额外的dp空间，O(1)空间就可以。看了看代码，和第一个解法一样，所以我感觉之所以第一个不容易理解，是因为我并没有透彻理解，来，再来一次。

关键点：

maxSubArray(A, i) = maxSubArray(A, i - 1) > 0 ? maxSubArray(A, i - 1) : 0 + A[i]; 

务必注意：不是从头开始的，是任意的截止到i的子序列的最大和

package com.card;

class GFG {



    //sofar 小于curren开始，大于curr结束，由此计算索引
    static int maxSubArraySum(int nums[]) {
        int res=nums[0];
        int currentMax = nums[0];
        for (int i = 1; i < nums.length; i++) {
            currentMax=nums[i]+(currentMax>0?currentMax:0);
            res=Math.max(res,currentMax);
        }
        return res;
    }

    /* Driver program to test maxSubArraySum */
    public static void main(String[] args) {
        int a[] = {-2,1,-3,4,-1,2,1,-5,4, 1};
        int max_sum = maxSubArraySum(a);
        System.out.println("Maximum contiguous sum is "
                + max_sum);
    }
}