【数据结构】最短路径问题

从一个源点出发求到每一个顶点的最短路径

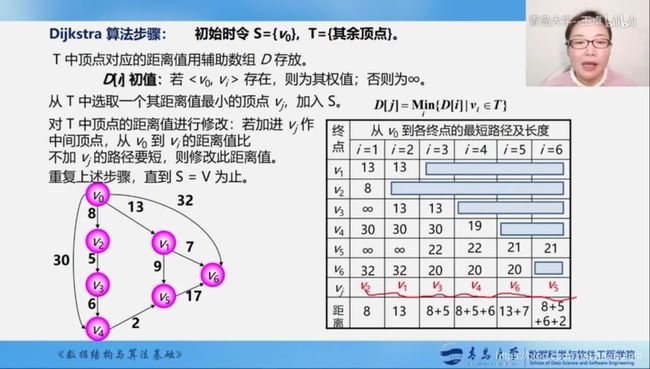
求解这个问题的时候我们用到Dijkstra算法，算法的描述如下：

（1）首先定义一个数组用来存储从源点到每一个顶点的最短路径（不可达用无穷表示），使用S集合来储存已经求得最短路径的顶点，那么剩余顶点就存放在集合T中

（2）第一次迭代的时候S只有源点，然后根据S集合中的顶点来更新最短路径数组D中的值，每次选择不在集合S中且路径最短的顶点加入集合S

（3）根据集合S的顶点更新最短路径，如果D[j] + arc[j][k] < D[k] , 那么D[k] = D[j] + arc[j][k]

（4）执行n-1次（2）和（3）就可以得到源点到所有顶点的最小路径了

一个鲜活的例子

代码实现

//最短路径问题之Dijkstra算法//
typedef int Pathmatirx1[MAXVEX]; //用于记录最短路径所经过的路径下标
typedef int ShortPathTable1[MAXVEX];//用于记录起始点到下标顶点的最短路径权值
 
//算法主体
void ShortestPath_Dijkstra(MGraph *G, int v0, Pathmatirx1 *P, ShortPathTable1 *D) {
	int v, w, k, min;
	int final[MAXVEX];//用于记录顶点是否被纳入最短路径，纳入为1，否则为0
	for (v = 0; v < G->Vertex_num; v++) {
		final[v] = 0;
		(*D)[v] = G->arc[v0][v]; //填入v0与各点间的权值
		(*P)[v] = 0;			 //初始化路径
	}
	//初始化第一个顶点
	(*D)[v0] = 0;   //第一个顶点到第一个顶点的权值为0
	final[v0] = 1;  //表示第一个顶点已经加入最短路径
	//开始主循环，求v0到各个顶点的最短路径
	for (v = 1; v < G->Vertex_num; v++) {
		//从1号顶点开始
		min = INFINITY;
		for (w = 0; w < G->Vertex_num; w++) {
			if (final[w] == 0 && (*D)[w] < min) {
				//如果这个顶点没有加入最短路径并且v0到这个顶点的路径最短
				k = w;
				min = (*D)[w];
			}
		}
		//出循环的时候已经找到了目前可以达到的最短路径
		final[k] = 1;
		//接下来更新最短路径表
		for (w = 0; w < G->Vertex_num; w++) {
			if (final[w] == 0 && (min + G->arc[k][w]) < (*D)[w]) {
				//如果该顶点没有纳入最短路径并且v0到这个顶点路径比之前的要短的话
				(*D)[w] = min + G->arc[k][w];//更新最短路径（v0到w）
				(*P)[w] = k;				 //存放前驱顶点(k到w)
			}
		}
	}
	//打印最短路径
	printf("最短路径为：\n");
	for (v = 1; v < G->Vertex_num; v++) {
		printf("（%d，%d）\n", (*P)[v], v);
	}
}

存储方式为邻接矩阵

求每一对顶点之间的最短路径

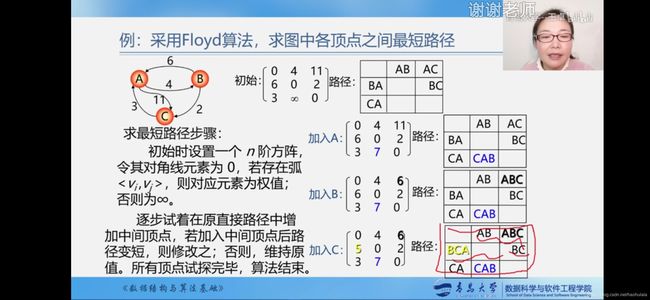
Dijkstra算法的时间复杂度为O(n^3)，还有一种时间复杂度也是O(n^3)的算法，叫做Floyd算法。

算法的描述如下：

先初始化一个邻接矩阵用来存储每个路径之间的距离，然后每次加入一个顶点，重新计算每个顶点间的最短路径，知道加入了n个顶点为止，最后得到的矩阵D^(k-1)就是最终得到的最短路径。

我记得离散数学图论中说邻接矩阵的n次方表示每个顶点到每个顶点中间顶点的序号不大于n的最短路径，不知道我有没有记错。

一个鲜活的例子

代码实现

//最短路径问题之Floyd算法//
typedef int Pathmatirx[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];
 
void ShortestPath_Floyd(MGraph *G, Pathmatirx *P, ShortPathTable *D) {
	int v, w, k;
	//先初始化距离矩阵和路径矩阵
	for (v = 0; v < G->Vertex_num; v++) {
		for (w = 0; w < G->Vertex_num; w++) {
			(*D)[v][w] = G->arc[v][w]; //直接用权值初始化距离矩阵先
			(*P)[v][w] = w;            //用终点顶点的下标初始化路径矩阵
		}
	}
	//接下来开始主循环
	//最外层循环为中间路径
	//中间循环为起始点
	//最里层循环为终点
	for (k = 0; k < G->Vertex_num; k++) {
		for (v = 0; v < G->Vertex_num; v++) {
			for (w = 0; w < G->Vertex_num; w++) {
				if ((*D)[v][w] > (*D)[v][k] + (*D)[k][w]) {
					//如果经过中间点的距离更短的话
					(*D)[v][w] = (*D)[v][k] + (*D)[k][w];
					(*P)[v][w] = (*P)[v][k];  //这是路径v到w的下一个顶点是v到k所存顶点
				}
			}
		}
	}
	//打印距离矩阵
	printf("距离矩阵为：\n");
	printf("\t");
	for (v = 0; v < G->Vertex_num; v++) {
		printf("V%c\t", G->vexs[v]);
	}
	printf("\n\n");
	for (v = 0; v < G->Vertex_num; v++) {
		printf("V%c\t",G->vexs[v]);
		for (w = 0; w < G->Vertex_num; w++) {
			printf("%d\t", (*D)[v][w]);
		}
		printf("\n\n");
	}
	printf("\n\n");
	//打印路径矩阵
	printf("路径矩阵为：\n\t");
	for (v = 0; v < G->Vertex_num; v++) {
		printf("V%c\t", G->vexs[v]);
	}
	printf("\n\n");
	for (v = 0; v < G->Vertex_num; v++) {
		printf("V%c\t",G->vexs[v]);
		for (w = 0; w < G->Vertex_num; w++) {
			printf("%d\t", (*P)[v][w]);
		}
		printf("\n\n");
	}
	printf("\n");
	//打印最短路径
	for (v = 0; v < G->Vertex_num; v++) {
		for (w = v + 1; w < G->Vertex_num; w++) {
			printf("V%d-V%d weight：%d\t", v, w, (*D)[v][w]);
			k = (*P)[v][w];
			printf("Path：V%d", v);
			while (k != w) {
				//当k不是终点的时候
				printf(" -> V%d", k);//打印下一个顶点
				k = (*P)[k][w];     //继续寻找下一个顶点
			}
			printf(" -> V%d", w);
			printf("\n");
		}
		printf("\n");
	}
}