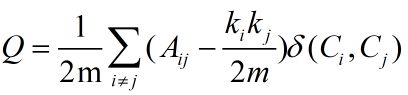Neo4j笔记（一）算法（2）算法实例

一、中心度算法

1、PageRank

1.1  算法介绍

PageRank最初是谷歌推出用来计算网页排名的，简单的说就是，指向这个网页的链接数越多，那么这个网页就越重要。但是很可能会有人自己制作一些垃圾网页设置大量的链接指向自己的网页来提高网页排名，这肯定是谷歌不希望看到的。因此PageRank还有一个迭代计算的过程，一个网页A虽然有大量的垃圾网页指向自己，但是这些垃圾网页是没有被指向的，因此迭代完以后A的得分也不会高。因此PageRank的计算基于两个假设：
（1）数量假设：一个节点（网页）的入度（被链接数）越大，页面质量越高
（2）质量假设：一个节点（网页）的入度的来源（哪些网页在链接它）质量越高，页面质量越高

PageRank在迭代之前会为每个网页赋予一个相同的初始值，假设有A、B、C、D四个网页，B、C、D都只指向A，则迭代一次以后A的PageRank值：PR(A) = PR(B)+PR(C)+PR(D)。如果B除指向A以外还指向另一个网页，D不指向A，则：PR(A) = PR(B)/2+PR(C)。

PageRank计算公式：

（1）PR(A) 是页面A的PR值。
（2）PR(Tn)是页面Tn的PR值，在这里，页面Tn是指向A的所有页面中的某个页面。
（3）C(Tn)是页面Tn的出度，也就是Tn指向其他页面的边的个数。
（4）d 为阻尼系数，其意义是，在任意时刻，用户到达某页面后并继续向后浏览的概率，该数值是根据上网者使用浏览器书签的平均频率估算而得，可以设置在0和1之间，通常d=0.85。d的引入也和终止点问题、陷阱问题有关。
（5）关于PageRank的计算公式，存在不同版本，仅供参考。

PageRank的缺点：
第一， 没有区分站内导航链接。 很多网站的首页都有很多对站内其他页面的链接， 称为站内导航链接。 这些链接与不同网站之间的链接相比，肯定是后者更能体现PageRank值的传递关系。 
第二， 没有过滤广告链接和功能链接（例如常见的“分享到微博”）。这些链接通常没有什么实际价值， 前者链接到广告页面， 后者常常链接到某个社交网站首页。 
第三， 对新网页不友好。一个新网页的一般入链相对较少，即使它的内容的质量很高，要成为一个高PR值的页面仍需要很长时间的推广。

由于本文的目的不是介绍PageRank的原理，因此对于PageRank的介绍比较简单，PageRank的详细知识请参阅其他资料。

1.2  Neo4j PageRank

关于算法的配置和官方地址，请参考前一篇文章。

语法
algo中的算法都以过程形式调用，语法如下：

CALL algo.pageRank(label:String, relationship:String,
    {iterations:20, dampingFactor:0.85, write: true, writeProperty:'pagerank', concurrency:4})
YIELD nodes, iterations, loadMillis, computeMillis, writeMillis, dampingFactor, write, writeProperty

字段含义如下：

名称	类型	默认	是否可选	含义
label	string	null	yes	加载的节点标签，如果为null，加载所有节点
relationship	string	null	yes	加载的关系类型，如果为null，加载所有关系
iterations	int	20	yes	迭代次数，默认20
concurrency	int	available CPUs	yes	并发数量，默认CPU数
dampingFactor	float	0.85	yes	阻尼系数，默认0.85
weightProperty	string	null	yes	权重属性，pagerank既支持无权重，也支持有权重，默认无权重计算，该属性必须是数值型
defaultValue	float	0.0	yes	权重的缺省值，如果某个关系没有指定的权重属性或者类型不对，则使用该值替代
write	boolean	true	yes	是否将计算结果回写为节点属性，对于数据量很大的时候比较适用。一次计算，永久查询
graph	string	'heavy'	yes	使用label和关系类型指定数据集的时候使用'heavy'；使用cypher语句指定数据集的时候（例如使用match匹配结果集）使用'cypher'；默认计算有20亿个节点和20亿个关系的限制，如果图超过这个限制，使用'huge'

对于不熟悉的属性，建议都使用默认值。另外，Neo4j还支持以结果流的形式运行PageRank，不会回写到节点属性中，比较适合查看、调试：

CALL algo.pageRank.stream(label:String, relationship:String,
    {iterations:20, dampingFactor:0.85, concurrency:4})
YIELD node, score

Demo
流结果计算：

CALL algo.pageRank.stream('Page', 'LINKS', {iterations:20, dampingFactor:0.85})
YIELD nodeId, score

RETURN algo.getNodeById(nodeId).name AS page,score
ORDER BY score DESC

回写计算：

CALL algo.pageRank('Page', 'LINKS',
  {iterations:20, dampingFactor:0.85, write: true,writeProperty:"pagerank"})
YIELD nodes, iterations, loadMillis, computeMillis, writeMillis, dampingFactor, write, writeProperty

加权计算：

CALL algo.pageRank.stream('Page', 'LINKS', {
  iterations:20, dampingFactor:0.85, weightProperty: "weight"
})
YIELD nodeId, score

RETURN algo.getNodeById(nodeId).name AS page,score
ORDER BY score DESC

Personalized PageRank：
Personalized PageRank是PageRank的变体，偏向于一组sourceNodes

MATCH (siteA:Page {name: "Site A"})

CALL algo.pageRank.stream('Page', 'LINKS', {iterations:20, dampingFactor:0.85, sourceNodes: [siteA]})
YIELD nodeId, score

RETURN algo.getNodeById(nodeId).name AS page,score
ORDER BY score DESC

二、社区检测算法

1、Louvain

1.1  Modularity

        Modularity（模块度）函数最初被用于衡量社区发现算法结果的质量，它能够刻画发现的社区的紧密程度。模块度函数是由Newman和Girvan在2004年提出的一种用于评估社区划分的全局目标函数，既然能刻画社区的紧密程度，也就能够被用来当作一个优化函数，其定义公式如下：

其中m为图中边的总数量，A为邻接矩阵，如果是无权图，所有边的权重可以看做是1。 表示节点 i 的度，计算方法是所有与 i 相连的边的权重和。 表示节点 i 所属的社区。的定义如下：

Modularity函数可以化简如下：

表示社区c内边的权重之和，表示与社区c内的节点相连的边的权重之和。化简过程可以这么理解，如果 i 和 j 属于不同的社区，则 ，只考虑 i 和 j 属于同一个社区的即可得到化简结果。基于模块度的社区发现算法，都是以最大化模块度Q为目标。

1.2  算法介绍

Louvain算法由鲁汶大学的作者在2008年提出的，原始论文是《Fast unfolding of communities in large networks》。Louvain算法是一种基于多层次优化Modularity的算法，它的优点是快速、准确，被认为是性能最好的社区发现算法之一。Louvain算法的过程如下：

（1）将图中的每个节点看成一个独立的社区，社区的数目与节点个数相同。
（2）遍历网络中的每个节点 i，依次尝试把节点 i 分配到其每个邻居节点所在的社区，计算分配前与分配后的Modularity变化，并记录变化最大的那个邻居节点，如果Modularity变化是正的，则把 i 分配到前面记录的邻居节点社区中，如果Modularity变化都是负的，则所有节点所属社区都不变。
（3）重复（2），直到所有节点的所属社区不再变化。
（4）对（3）中形成的社区进行折叠，把属于同一个社区的节点压缩成一个新节点。压缩方法就是，社区内节点之间的边的权重和转化为新节点的环的权重（新的节点 i 和自身之间也存在了一个权重），社区间的相邻公共边权重和转化为新节点间的边权重。
（5）重复（1）~（4），直到整个图的Modularity不再发生变化。

1.3  Neo4j Louvain

关于算法的配置和官方地址，请参考前一篇文章。

语法

CALL algo.louvain.stream('User', 'FRIEND', {})
YIELD nodeId, community
RETURN algo.asNode(nodeId).id AS user, community
ORDER BY community;

上述程序计算User标签和FRIEND关系组成的图社区分布，并以流结果直接输出，不会回写到Neo4j中。

CALL algo.louvain('User', 'FRIEND',
  {write:true, writeProperty:'community'})
YIELD nodes, communityCount, iterations, loadMillis, computeMillis, writeMillis;

上述程序计算User标签和FRIEND关系组成的图社区分布，并将每个节点所属的社区以属性形式保存到图中，社区属性是community。

1.4  分层Louvain算法

根据前边原理可以知道，Louvain算法本身就是一个不断折叠、聚合的过程。分层Louvain算法不仅可以显示最终的社区检测结果，而且可以看出不同层级的社区检测结果。

CALL algo.louvain.stream('User', 'FRIEND', {includeIntermediateCommunities: true})
YIELD nodeId, communities

RETURN algo.asNode(nodeId).id AS user, communities
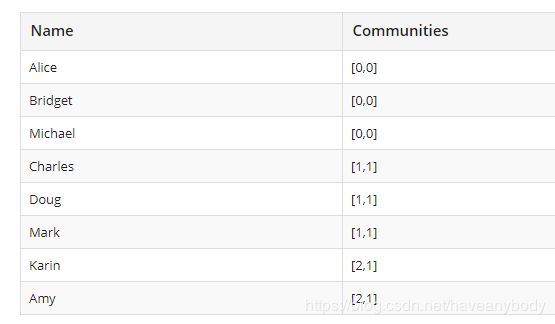
ORDER BY communities;

通过设置includeIntermediateCommunities参数，可以查看不同层级的社区。上面结果显示如下：

可以发现第一级有三个社区，第二级有两个社区。

1.5  半监督Louvain算法

前面介绍的Louvain算法都是无监督的。如果已知某些节点是联系比较紧密，是同一个社区的，Louvain算法也可以先给这些节点预定义社区标签，变成半监督Louvain算法。

CALL algo.louvain.stream('User', 'FRIEND', {communityProperty: 'community'})
YIELD nodeId, communities

RETURN algo.asNode(nodeId).id AS user, communities
ORDER BY communities;

在上述程序中，我们给部分节点预定义了一个社区标签，属性名称是community，